IIR数字滤波器的FPGA实现

一、关于IIR数字滤波器

当然关于IIR滤波器的知识，想必大家在教材上都已经很熟了，这里我就简单说一下自己的理解好了。

正如前面说的，IIR数字滤波器，即无限长单位脉冲响应数字滤波器。所谓无限长单位脉冲响应，也就是说，对于一个系统，我们给其输其激励，在输出端得到的一串序列hn是无限长的，又因为我们讨论的都是因果系统，即只考虑n大于零的部分，所以，hn可以表示为0《= hn 《 无穷大。

前面还说了，IIR区别于FIR滤波器的还一个特点就是他的反馈结构，即IIR滤波器的输出，不仅与输入激励有关，还与当前的输出值也有关，用差分方程来表示就是

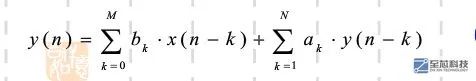
根据这个差分方程可以看出：

1、跟FIR滤波器的差分方程进行对比的话会发现，IIR滤波器的差分方程等式右边的前半部分跟FIR滤波器的差分方程类似，都是对输入信号进行的卷积运算，只不过FIR滤波器是将输入信号与系统的单位脉冲响应进行卷积，而这里是输入信号跟IIR滤波器的零点系数进行卷积

2、后半部分是IIR滤波器的极点部分，也可以看做是一个N阶的FIR滤波器，运算对象是系统的输出信号的一部分与极点系数的一部分。

3、因此，IIR滤波器的输出就可以看成是 两个FIR滤波器的运算，即

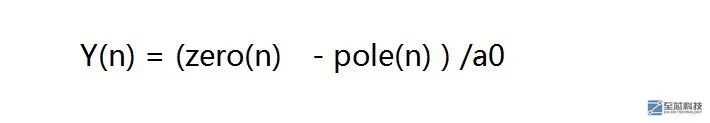
ao即Y（n）的系数

然而IIR滤波器的表示形式还有一种方式，就是我们常说的系统函数，即对差分方程中的输入输出进行Z变换，并通过移位运算得到H（z），而它也就是系统单位脉冲响应的Z变换

二、关于零极图

我们知道，系统函数的分子分母都是一个乘加多项式，既然这样，分子分母就可以进行因式分解，也就是我们书本上的系统的零极点表达式

零极图的作用可不小，既然我们滤波器的系统函数完全可以用零极点来表示，也就是说，我们滤波器的性质，也可以通过零极图来分析，比如可以通过零极图来看系统的单位脉冲响应的形状，系统的因果性与稳定性之类的

1、零极图与单位脉冲响应

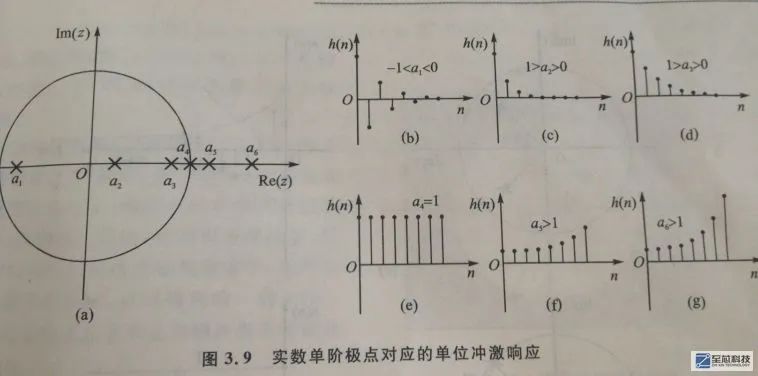
看上面这张图，现在假如有个IIR数字滤波器，假设只有一个极点，极点位置的不同会导致滤波器单位脉冲响应形状的不同，总结如下：

1、极点在单位圆内时，单位脉冲响应的形状呈下降收敛状，极点在单位圆上时，单位脉冲响应的形状呈直线状，极点在单位圆外时，单位脉冲响应的形状呈上升发散状，且离单位圆越远，放大倍数越大

2、单位脉冲响应的形状主要是由滤波器的极点位置决定，零点位置主要是影响单位脉冲响应的幅度特性和相位特性（上图中虽然没有画出零点，大家可以通过matlab仿真总结出这条结论）

2、零极图与滤波器的因果性，稳定性

通过教材我们已经知道了，我们所研究的都是因果系统，而因果系统的收敛域不包括任何一个极点。为什么呢？因为极点是导致系统函数趋于无穷大的点，一旦收敛域包含了极点，那就会导致系统函数不收敛，因此，因果系统的收敛域必须大于离单位圆原点最远的那个极点，也就是说，只要知道了一个因果系统的极点分布，那么他的收敛域也就已经确定了。假如定义一个系统的极点分别为 ： 1 ，-2，0.5，-3，那么这个系统的收敛域就是 z 》 3.

关于稳定性问题，我们知道，只有当系统函数的收敛域包含单位圆的时候，单位脉冲响应绝对可和，这时候系统才是稳定的，又由于之前说的因果性， 系统函数的收敛域不能包含任何一个极点，因此我们知道，只有当极点在单位圆内的时候才符合要求，因此，极点在单位圆内成了系统稳定的必要条件。

三、关于IIR滤波器的设计方法

其实，我们书本上介绍的什么脉冲响应不变法，双线性变换法之类的设计方法，设计过程都太过于繁琐，想必大家都深有体会，可能原理不是很难理解，但是真正让我们去手动去算一个题，还不知道要算到什么时候。但是matlab为我们提供好了设计函数，我们甚至不需要知道那些变换方法，也可以设计出符合要求的滤波器。但是，书本上既然写了，总有他写这些东西的目的，可能我们实在不好理解他的运算过程，但是也要大体上知道这回事，毕竟人家是当时的科学巨匠的毕生心血，哪有那么好懂~是吧，我们只要是会用就不错了，下面就简单总结一下这几种方法：

IIR数字滤波器都是经过低通模拟滤波器变换而来的，因为模拟滤波器的理论已经很成熟了，而且有大量的数据供我们直接使用，比如巴特沃斯滤波器的设计过程，已经给我提供好了求最小滤波器阶数和零极点的公式，只要我们将滤波器指标带进去计算就好了。

至于这些公式怎么来的，说实话我也看不懂，只知道是一大片数学公式推导而来，很多朋友一看到这群数学公式肯定就迷糊了，甚至是失去了学习的兴趣了，太过繁琐的数学公式的推导，使得我们的教材变得枯燥无味，我是过来人我深有体会，虽然这样的教材很严谨，但是却抹杀了学生的积极性，并没有取得好的教学目的，其实还是感觉那句老话说的对“高手在民间啊”，很多一些不出名的关于信号处理的书，却硬是把信号处理这门课写的生动有趣，让人一读便懂，甚至有种豁然开朗的感觉。再反观我们使用的教材，虽然获得了什么什么教学奖，然而感觉并没有真正站在学生的角度在写这本书，学生看到只是大片的数学公式，也就丧失了信心了。

常用的模拟滤波器设计模型大概有这几种，巴特沃斯滤波器，切比雪夫滤波器、和椭圆滤波器，这几个滤波器都模拟低通滤波器，要想得到其他类型的滤波器，需要经过变换，然而这几种提供了详细的设计资料，有了这些资料，我们就能通过变换将其变换为我们需要的其他类型的数字滤波器。

例如，我想设计一个IIR带通滤波器，根据需要

1、 我需要先确定滤波器指标，主要包括通带最大衰减，阻带最小衰减，通带截止频率，阻带截止频率

2、有了这4个模拟带通滤波器的指标，我们可以用频率变换公式将这4个指标转换为相应模拟低通滤波器的指标。

3、有了低通滤波器的指标，就可以根据经典滤波器的资料，设计成相应的模拟低通滤波器。

4、 对模拟低通滤波器进行频率变换，得到我们想要的模拟带通滤波器

5、最后可以通过脉冲响应不变法或者双线性变换法，得到我们需要的数字带通滤波器

下面就总结一下这两种变换方法

脉冲响应不变法

上面说了，需要通过脉冲响应不变法或者双线性变换法将模拟带通滤波器转换为我们需要的数字带通滤波器。既然是模拟滤波器，也就是说，是单位脉冲响应ht的拉普拉斯变换，如果对模拟滤波器的系统函数进行逆拉普拉斯变换就可以得到ht，有了ht，再通过抽样不就可以转化为hn了嘛，所以，脉冲响应不变法可以总结如下：

1、对模拟滤波器的系统函数进行逆拉普拉斯变换得到时域上连续的系统的单位冲激响应ht

2、对ht进行n点等间隔抽样，得到时域上离散的系统的单位脉冲响应hn

3、对hn进行Z变换，得到数字滤波器的系统函数H（Z）

需要注意的是，在对时域上连续信号进行等间隔抽样的时候，我们知道，时域抽样等同于频域的周期延拓，如果不满足一定的条件，就会导致信号的频域混叠 ，而这个条件，就是我们采样定理所给出的，即必须得保证模拟滤波器的带宽是有限带宽，并且采样频率fs 》 2fmax.

看下面这张图我来解释一下

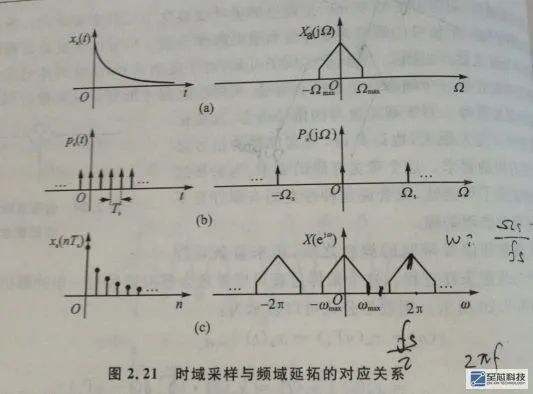
这里我来解释一下采样定理，假如有一个带限模拟信号，他的时域和频域波形如图第一排所示，可以看到在频域，他的带宽为2Ωmax，即最大角频率为Ωmax

而Ωmax= 2πfmax，这里的fmax是模拟频率，单位是hz，跟角频率不同

现在用一个频率为fs的信号对原模拟信号在时域进行等间隔抽样，采样信号在频域的波形如图第二排所示，角频率Ωs = 2πfs，是一个周期为Ωs的周期信号

图上第三排是模拟信号经采样后的时域波形与频域波形，时域波形很直观，就是由连续信号变为了离散信号，频域波形变成了原模拟信号波形的周期延拓，周期为2π

大家知道，在数字频域，角频率w = Ω / fs ，所以我们看到在Ωs的正下方对应的是2π，数字频域0到2π之间对应的当然就是π，而这里的π对应的模拟频率，当然就是fs/2，而数字频域的wmax 则对应 Ωmax / fs ，即 wmax = 2πfmax / fs

所以，要想保证经采样后的信号的频谱不发生频率混叠，就必须要保证wmax 《 π

因此推得 fs 》 2fmax

正是因为如此，脉冲响应不变法只能用来设计低通和带通滤波器，不能设计高通和带阻滤波器，因为后两者在数字频域π处均存在频谱分量

双线性变换法

双线性变化法相对于脉冲响应不变法适应性更强，不存在混叠失真的情况，但是计算过程也是相当的复杂，具体过程其实书上都有写，只不过就是太过繁琐，让人看得不爽。好在matlab为我们提供了设计好的函数，matlab工具箱里的函数 butter ellip cheby1 cheby2 等函数都是基于双线性变换法来设计的函数，可以直接将跳过复杂的设计过程，由我们制定的滤波器指标直接生成数字滤波器的零极点系数。

既然这样，我们之前还那么多废话干什么？直接讲matlab设计不就好了？其实并不是这样，知识是一个体系，只有有了前面的知识做铺垫，才能为以后的设计打下基础，要不然只会调用matlab函数，不懂为什么这样的，到后面就遇到瓶颈了。

好了，在了解这些理论知识之后我们就可以来设计我们的滤波器，其实当这些东西都掌握的差不多的时候，你会发现设计滤波器并不是很难

和FIR滤波器一样，我先把滤波器要求说明一下，然后再按照设计要求进行设计

四、IIR滤波器的matlab设计与FPGA实现

要求设计一个IIR低通数字滤波器，要求：：

1、 设计成切比雪夫II型滤波器

2、截止频率为500hz，阻带最小衰减为60db，采样频率为2000hz，，滤波器阶数为7

3、合成信号为100，500，800hz的正弦信号的叠加

4、要求分别采用直接II型结构和级联型结构分别在FPGA上实现，并通过modelsim仿真出滤波后的100HZ正弦波

5、级联结构为了提高运行速度采用流水线结构设计

6、通过matlab对modelsim输出的数据进行仿真，看是否符合要求

前面说过了，matlab为我们提供了IIR滤波器设计的工具箱，我们可以直接调用函数，就可以直接由滤波器指标设计成数字滤波器

如上图所示，我们直接调用cheby2型函数，送人滤波器设计指标，直接就可以设计出符合要求的滤波器，可以说，就这么几行代码，一个滤波器就设计完成了。但是，我们不仅要设计出滤波器，还要实现它，并且是FPGA硬件实现，光有这些数据是不行的，上面设计的滤波器输出如下

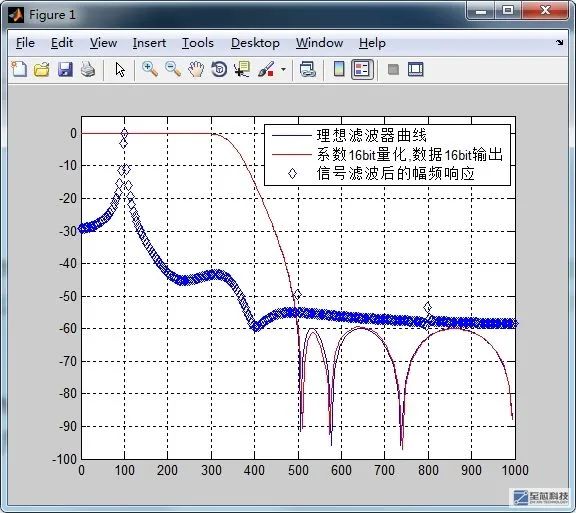
可以看到，这些数据是无法在FPGA上实现的，我们需要将他们量化，具体进行多少bit的量化才可以设计出符合要求的滤波器，需要通过matlab仿真才知道。当然，由上面的系数构成的滤波器是理想滤波器，当然他们的位数不仅仅是这几位，是因为matlab显示的原因，后面还有很多位数没有显示出来，要知道，我们是要将这些数据送到FPGA内部的寄存器中进行运算的，不可能将所有位数都表示完整，只能表示个近似值，这就导致了有限字长效应，使得实际滤波器与理想滤波器还是有些差别的，因此，我们需要将这些系数进行量化，将量化后的滤波器系数求出幅频响应，与理想滤波器的幅频响应进行对比，来确定量化位数

上图就是通过仿真来确定滤波器的量化位数，函数QuantIIRDirectArith是用来计算实际情况下滤波器的单位脉冲响应的，是人为编写的函数，其中的算法我们可以不去深究，只知道输入量化后的滤波器系数和需要滤波器输出的位数，就可以计算出实际滤波器的输出情况，与理想滤波器进行对比，从而确定量化位数，这里仿真出来，当量化位数为16的时候，波形就几乎与理想情况吻合

对于系数的量化问题，这里也不能像FIR滤波器一样直接进行量化了，因为IIR滤波器不仅存在乘加运算，还存在除法运算。前面说了，IIR滤波器的输出，可以看做是两个FIR滤波器相减之后再除以系数a（0），这里的系数a（0） 就是极点系数的第一项，既然要除以这个系数，只要保证这个系数是2的整数次幂，就可以通过向右移位的方式来进行相除。例如，经过处理和量化之后，极点系数的第一项为1024，那么就相当于把两个FIR滤波器的运算结果右移10位就好了

这也可以算是一种算法了，大家可以带一个数进去试试，就知道这种算法的原理了，经过这种方式的量化后，我们得到的滤波器系数就变为

从这量化后的系数我们可以看出，零点部分完全就是一个FIR滤波器，极点部分还不太像，因为系数不对称，这样的话，我们有了滤波器的零极点系数，剩下的就是FPGA实现了。

对于FPGA的实现过程，零点部分完全和FIR滤波器的运算过程相同，就是将输入信号存入寄存器之后，对输入信号进行对称系数累加，再分别与滤波器的零点系数进行相乘，最后将结果相加输出滤波器极点部分zero（n）

极点部分跟零点部分类似，只有一点稍微需要注意，由于IIR滤波器存在反馈结构，滤波器的输出也是极点部分的输入。极点部分的累加相乘跟零点部分稍有不同，首先，极点部分不存在对称结构，因此不需要将输入信号进行对称相加，只需要直接与极点系数相乘。还有就是，极点系数的第一项不参与相乘，因为他是输出Y（n） 的系数，从第二项开始才进行乘加运算，例如pole_coe（1）*y（n-1） ， pole_coe（2）*y（n-2）。..。..。.

前面说过，零点部分与极点部分进行减法运算，结果再除以Y（n）的系数之后，就是IIR滤波器的输出

在用FPGA实现IIR滤波器的时候要注意这几点，我总结如下

1 、 首先要注意，不管是存储数据的寄存器型变量还是线型变量都不要忘记定义成有符号型数据

2、 要注意字长问题，两个N位数据相加，至少需要N+1位寄存器存储结果才能保证结果不溢出，两个N位数据相乘，至少需要2N位寄存去存储，大部分情况下，2N-1位就可以了

3、最后的截尾处理，如果不能够保证截取的位数能够将输出的数据完整表示，可以考虑放弃精度，舍弃低位取高位。例如上面，假如我截取sum_div的0到15位不能够表示IIR滤波器的输出，也就是说有些IIR滤波器输出的数据要大于2^15，因此，截尾的时候可以考虑截取1到16位作为结果，这样做话相当于降低了量化位数，精度降低了，但可以保证输出正确幅度的波形

下面是将叠加信号进行滤波后的输出情况

五、级联结构的IIR滤波器的FPGA实现

其实在实际应用中，应用最广泛的还是级联型结构，因为这种结构的系统函数除了一个系数之外完全是由零极点构成，而且占用资源少，速度快。

级联结构说白了就是几个直接型结构的IIR滤波器相乘罢了，有了直接型结构的基础，再来设计级联结构就很简单了。

设计级联结构的关键一步就是如何将直接结构的滤波器系数转换为级联结构的系数，其实这也是一个算法问题，说实话这个算法我也没看明白，就是通过一系列的数学运算，将直接型结构转化为了级联结构的系数

可以看到，我们设计好直接型结构滤波器之后，直接调用转换函数，就可以得到级联结构的滤波器系数，其中b0为增益系数，就是放在零点部分外面的那个系数。转换函数是人为写的，我也不太懂为什么是这样转换的，既然别人已经做好了这种算法，我们实在看不懂的话就直接拿来用好了

函数Qcoe是量化函数，就是前面讲过的，要将极点系数量化为2的整数次幂的量化函数。

经过这样的处理之后，就会得到了四个直接型结构的IIR滤波器，每阶IIR滤波器的计算方法都跟前面直接型滤波器的计算方法相同，这里不做解释。

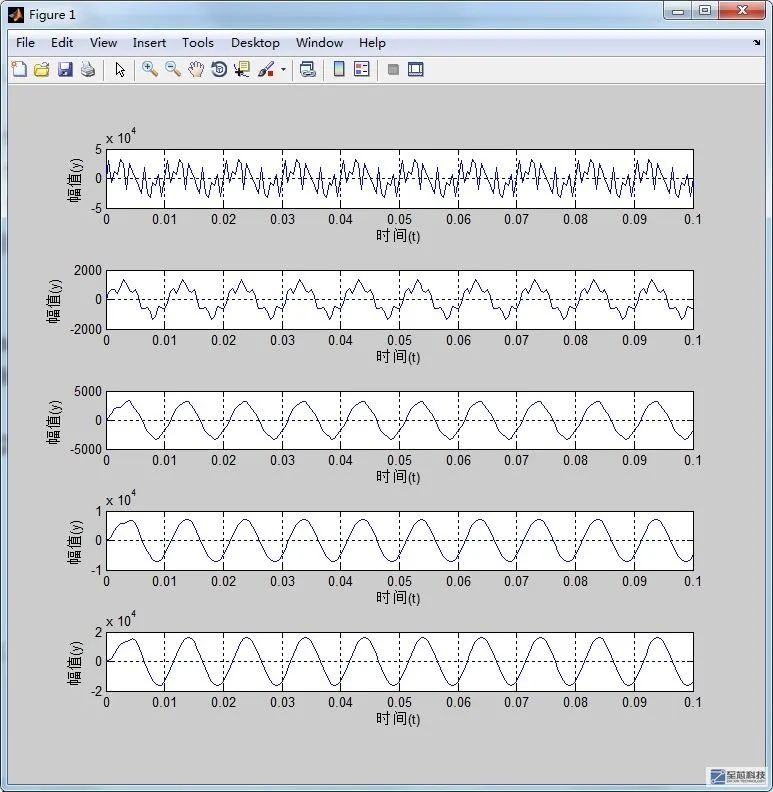
级联型结构在进行FPGA实现的时候要注意每一阶滤波器的输出数据的位宽，即通过matlab仿真出每级滤波器输出数据的最大值，算一下用多少位的寄存器才能表示这个数值，下面是合成信号依次通过各级滤波器，并计算每通过一级滤波器后的输出位宽

合成信号每通过一级滤波器，就相当于对信号进行了一次滤波，通过仿真可以看到，每通过一级滤波器，输出的信号更加趋于圆滑

级联结构的FPGA实现过程是比较费劲的，因为要设计多级滤波器，虽热每级滤波器的代码都是直接型滤波器，但其中的零极点系数的运算还是需要我们自己修改，而且还有仿真好每级滤波器的输出是否正常。但是没办法，因为IIR滤波器几乎没有IP核可以调用，我们也只能手写了

在进行零极点系数乘积运算的过程中，我们一方面可以调用乘法器来进行运算，另一方面可以利用移位的方式进行乘法运算

例如上图，474可以分解成几个2的整数次幂的形式的累加形式，因此，可以通过移位的方式实现乘法运算

采用级联方式实现FPGA的过程要注意的是每级滤波器的输出位数，保证每级滤波器的输出数据没有溢出，其他地方都跟直接型类似

至于采用流水线结构实现级联结构，就是在每级滤波器的输出部分加一个寄存器，每来一个时钟将数据输出，这一点很简单了，想必能看到这里的朋友对FPGA这点技巧还是很了解的。

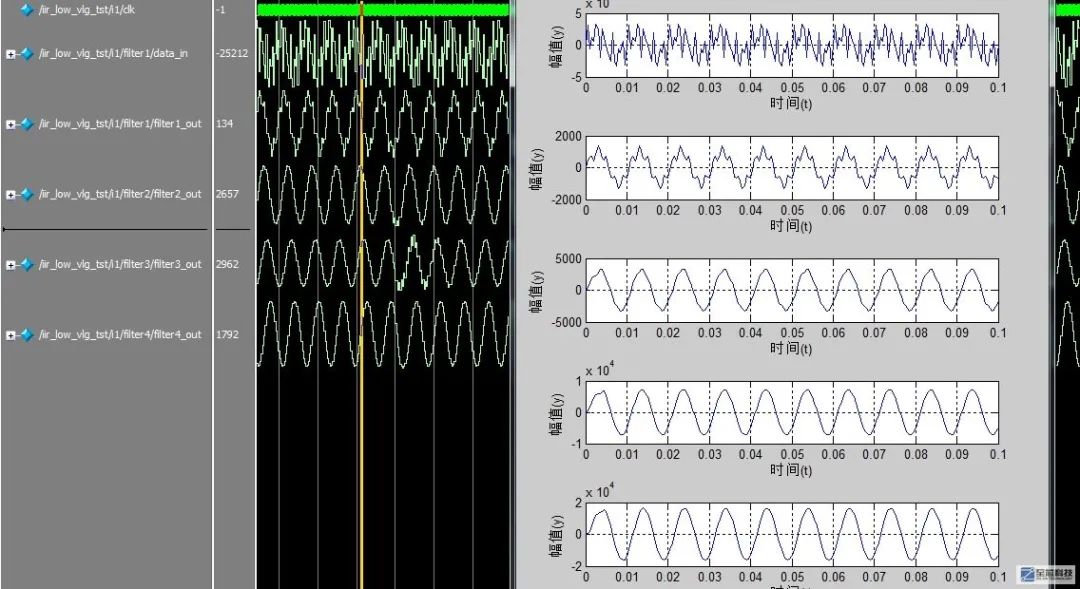
下面是modelsim仿真输出的各级滤波器的波形，与matlab仿真结果相比几乎相同，证明我们的结果是正确的

原文标题：零基础学FPGA（三十） IIR数字滤波器的FPGA实现笔记

文章出处：【微信公众号：FPGA设计论坛】欢迎添加关注！文章转载请注明出处。

责任编辑：haq