详解DSP的机载伺服控制系统设计

摘 要： 针对机载天线实时跟随头戴设备转动，提出了一种机载伺服系统的控制方案，系统以TMS320F2812 DSP为运算核心，通过RS-485连接绝对值光电编码器代替测速机对转台进行测速，并采用具有退积分饱和功能的数字PID增量型控制算法进行速度闭环控制，使系统具有了很好的动态性能和抗干扰性能。而且针对项目的实际还提出了一种先速度后位置的随动控制策略，经实际验证和测试，取得了很好的应用效果，不仅达到了系统的技术指标而且还提高了系统的鲁棒性。

伺服系统本质上就是一种随动系统，本文介绍的伺服系统为一维伺服转台，用于控制一种机载天线实时跟随另一种瞄准设备，时刻保持机载天线和瞄准设备在同一位置上，以达到微波系统通信的目的。瞄准设备电机运行速度常常不停变化，为使系统的输出以一定精度跟随瞄准设备的变化，与一般电机调速系统相比，其对转矩和速度的动静态控制特性要求要严格得多。

瞄准设备运行轨迹比较复杂，对伺服的跟踪性能的影响也比较大，该随动系统由于是机载设备，所以对整个伺服系统的结构尺寸和重量都做了非常严格的要求。加之微波天线波束窄，要保证伺服系统在跟随瞄准设备的过程中，能正常通信，高的定位精度和随动精度是必须要满足的指标。

因此，在整个伺服系统设计过程中，除了良好的结构设计外，要求相应的控制系统既要具有高性能的软硬件结构，又要有高性能[1]的控制策略和控制算法。本文着重介绍基于DSP的控制系统设计，并提出一种随动的控制策略，来保证伺服系统高的动态响应能力和静态稳定性，而且又有较强的抗干扰能力（即鲁棒性），使伺服系统达到整个系统的设计要求。

1 控制部分原理

控制系统部分硬件主要由控制模块和驱动模块两大部分组成。控制模块以TMS320F2812 DSP为运算核心，连同数字/模拟量转换模块（ADC）、以及两个RS-485收发器构成整个控制系统。基本原理框图如图1所示。

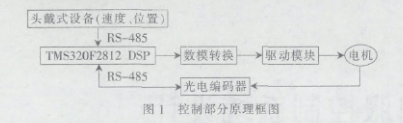
本伺服系统控制采用三闭环控制，即位置环、速度环和电流环[1]。其中，速度环的输出为电流环的给定信号，位置环的输出为速度环的给定信号；电流环和速度环是内环，位置环是外环。为了保证电流环的响应频带达到1 kHz以上，电流环采用硬件模拟电路实现，在此基础上进行速度闭环，能够达到很高的伺服精度，位置环和速度环的控制则在DSP控制器上通过算法实现。PID闭环的原理如图2所示。

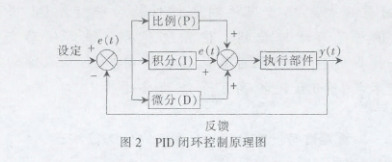
为了降低整机重量和成本，没有采用专门的测速机来进行速度闭环控制，测速通过一个绝对值的光电编码器提供的位置信息在DSP内部通过计算所得。绝对值光电编码器通过RS-485与DSP进行连接，DSP每毫秒给绝对值光电编码器发送一个握手信号采集绝对值光电编码器的位置信息数据，在绝对值光电编码器收到这个握手信号后把测到的位置信息回传给DSP，DSP获得这个位置信息后与上一毫秒的位置信息共同计算出一个速度值，进行速度闭环控制，电流环通过DSP把给定值送到D/A进行数字到模拟信号的转换后送给驱动模块。

2 退饱和数字PID控制算法

伺服系统是按误差控制的系统，适合采用PID控制算法，而根据硬件的实现方法有模拟和数字两种实现方法。本文中电流环用模拟电路实现保证有高的响应带宽，位置和速度则在DSP内用数字的方法实现。数字PID控制是比例、积分、微分调节的简称，是自动化领域性能最强的控制调节方法[2]。数字PID控制方法，具有控制简单、容易实现、算法灵活多变的特点。

PID的完整公式为：

u（t）=KP×e（t）+KI×e（j）+KD×[e（t）-e（t-1）]+u（0）（1）

其中，KP为比例放大系数；KI为积分放大系数；e（t）为误差；u（0）为控制量基准值（基础偏差）。

积分项是一个历史误差的累积值，如果只用比例控制时，要么就是达不到设定值，要么就会出现系统振荡，在使用了积分项后就可以解决达不到设定值的静态误差问题，例如一个控制中使用了PI控制后，如果存在静态误差，输出始终达不到设定值，这时积分项的误差累积值会越来越大，这个累积值乘上KI后会在输出的比重中越占越多，使输出u（t）越来越大，最终达到消除静态误差的目的。

实际情况中，在电动机的启动、停转或大幅度增减设定值时，短时间内系统会输出很大偏差，使得PID运算的积分积累很大，引起输出控制量增大和强烈的积分饱和效应，数字PID调节器中的积分饱和会引起大幅度的超调，使系统稳定性下降，所以消除积分饱和的关键在于不能使积分项过大，可以采用的方法有积分分离法、遇限消弱积分PID控制算法及变速积分PID算法等[5]。

为消除积分饱和带来的不利影响，系统采用带退饱和的积分分离法来防止积分饱和，积分分离的基本思路是：当被调量和设定值偏差较大时，取消积分作用，以免由于积分的作用使系统的稳定性下降，超调量增大，当被控制量接近给定值时，引入积分控制，以便消除静差，提高控制精度。当积分值积到设定的阈值时，清楚积分累积值，达到退积分的目的，提高系统的静态稳定性。

积分分离算法可表示为：

u（t）=KP×e（t）+?茁×KI×e（j）+KD×[e（t）-e（t-1）]+u（0）（2）其中β为积分项的开关系数。

β=1，|e（t）|≤ε0，|e（t）|>ε

ε为设定阈值。

3 控制策略及测试结果

本伺服系统通过接收瞄准设备传过来的位置和速度信息，进行跟随运动，让瞄准设备和伺服转台始终保持0.3°的随动误差，瞄准设备转动范围为-120°~+120°。瞄准设备间隔20 ms发一次位置和速度，伺服转台收到位置和速度后，必须在20 ms内跟上瞄准设备，并且瞄准设备和天线转台始终保持0.3°以内的位置误差。

为了使伺服转台能够始终跟上瞄准设备，这里采用了一种先位置后速度的跟踪控制策略，就是在转台控制DSP收到瞄准设备传过来的位置和速度后，先以一个瞄准设备速度的M（M>1）倍的速度走位置，当位置走到随动精度误差范围内（0.3°），再以瞄准设备的速度跟随瞄准设备。下一个20 ms来到后继续重复以上的算法步骤。在调试的过程中，主要调试M值，M值过小转台跟不上瞄准设备，M值过大则会出现天线转台过冲的情况，所以必须取一个合适的M值，以满足系统指标。图3是测试软件的主界面图。

测试软件主要完成对整个转台的各种指标进行测试和模拟真实观瞄设备的转动。

本文结合某项目的实际设计要求，设计了一种机载天线伺服转台的控制系统设计，控制系统基于TMS320F2812 DSP为运算核心，采用退积分饱和的PID算法对速度环和位置环进行校正，在实际实验的过程中，系统具有很好的动态性能和抗干扰性能。文中还着重介绍了一种伺服转台的随动控制策略，这种随动控制策略在某项目的实际应用中取得了很好的控制效果，文中经过反复的测试，给出了测试结果，这不仅提高了系统的动态性同时又增加了系统的鲁棒性。

参考文献

[1] 吴刚．车辆驾驶机械手的研制与伺服运动控制研究[D]．长春：吉林大学，2004．

[2] 孔慧勇．基于运动控制卡的全闭环控制系统研究[D]．成都：四川大学，2003．

[3] 王茂飞，程昱．TMS320C2000 DSP控制技术与应用开发[M]．北京：清华大学出版社，2007．

[4] 陈幼平，张代林，艾武，等．基于DSP的直线电机位置伺服控制策略研究[J]．电机与控制学报，2006，10（1）：61-65.

[5] 闫向勇，董志学，马蓓绯．基于LPC2368的模糊PID温度控制系统的设计[J]．电子测量技术，2009，34（3）：129-131．

[6] 黄玉钏，曲道奎，徐方，等．伺服电机的预测控制与比例-积分-微分控制[J]．计算机应用，2012，32（10）：2944-2947．

[7] 陈鹏．基于DSP的运动控制器开发及其运动控制算法研究[D]．长春：吉林大学，2007.

编辑：jq