一种新的静电发生器电路模型

0 引言

ESD（静电放电）是由于金属和非金属几何结构上电荷的积累，通常是摩擦起电。这种带电体直接或间接的相互作用是ESD放电发生的主要原因。ESD脉冲的泄放，使产品的软硬2种失效都有可能发生。所以电子产品对ESD的监测和防护是十分有必要的。系统级ESD测试的主要测试标准是国际电工委员会规定的IEC 61000-4-2。为了确保电子产品在遭受ESD脉冲时和ESD脉冲过后都能够继续正常工作，需要实施系统级ESD测试。在系统级ESD测试过程中，我们用ESD发生器（静电枪）来模拟ESD放电场景，但是频繁地进行实际系统级防静电测试是昂贵和耗时的过程，因此有必要寻求1种有效的方法来分析和预测设备的静电防护能力。

1 IEC61000-4-2标准

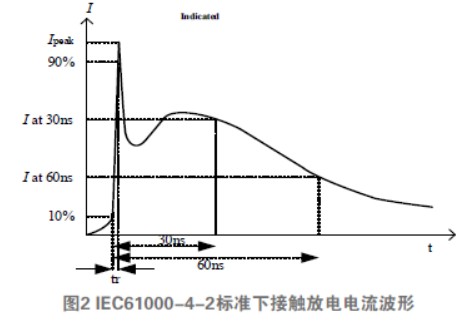
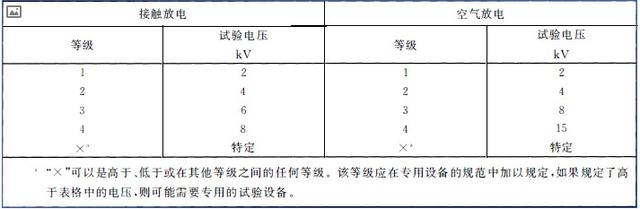
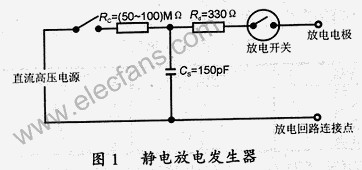
在IEC61000-4-2标准中，静电枪电路如图1所示，已充电的150 pF电容器通过330 Ω电阻放电，从而产生如图2所示的电流波形，该波形中有2个峰值。 根据测试电压，从（2~8） kV分为4个等级，每个等级相差2 kV，不同等级下对应的特性参数也不同。第1个峰值电流为3.75 kV/A，误差不得超过15％。30 ns的电流为2 kV/A，误差不大于30％，60 ns的电流为1 kV/A，误差小于30％。波形的上升时间占第一峰值电流的10％至90％，通常为0.8 ns，误差不能超过25％。然而这个误差范围相对较大，可能引起仿真结果的不准确。现存的电路模型精确度虽然有所提高，但与标准值还是有些差距。本文对电路模型进行优化后，在Cadence下进行模型的搭建与仿真，其输出波形的特征参数与标准值接近一致。

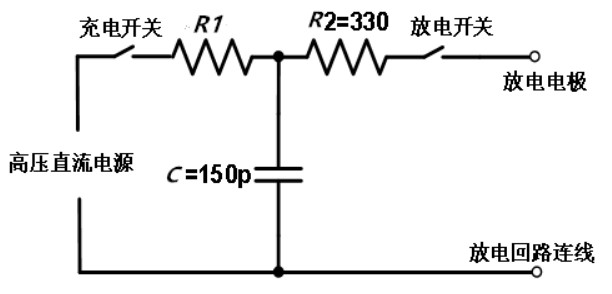
图1 IEC61000-4-2标准下接触放电电路简图

2 接触放电电路模型

2.1 数值计算

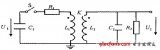
我国学者盛松林曾提出接触放电波形可以看做一大一小2个波组合而成，并且用数值表达式拟合出接触放电电流波形，但他的模型是基于度量的，没有电路特性。在电路上可以用2个不同的电容放电来形成这样的波，电路结构设计如图3所示。图4是静电枪电路的s域模型，设a点电压为Y（s），则可以列出a点的节点方程：

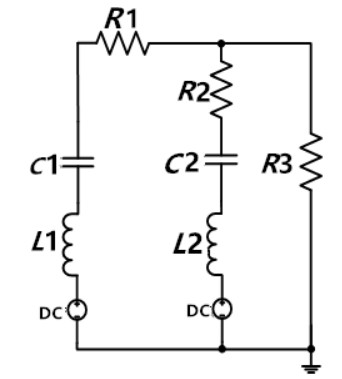
图3 接触放电模型电路原理图

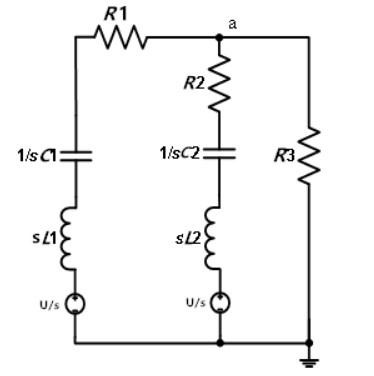
图4 s域电路模型

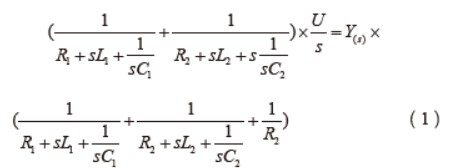
求出I（s），再进行拉普拉斯逆变换，最终求得时域中的电流I（t）。

通过计算发现，第1峰值的大小主要由R2、C2、L2决定，它会随着C2的增加，R2的减小而变大；第2峰值主要由R1、C1、L1决定，它会随着C1的增加，R1的减小而变大。R3为待测器件的阻值，一般是2 Ω。最终元件参数值如表1所示。

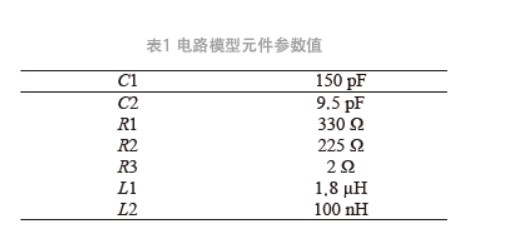
图5是电压为2 kV下的数值计算波形与实测波形的对比图（红色线是MATLAB下数值计算曲线，蓝色线是实测曲线），可以看出两者的吻合度是比较好的。波形的特征参数值如表2所示。

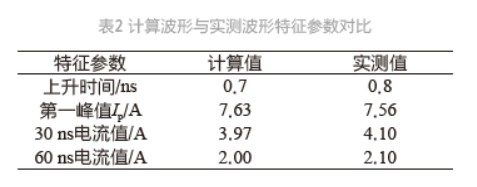
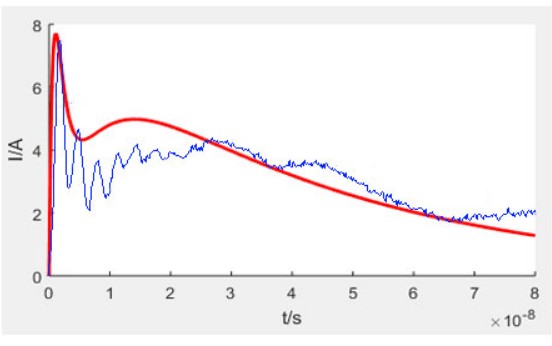
图5 2 kV下接触放电模型的数值计算与实测对比图

2.2 电路仿真

为了进一步验证模型的准确性，在Cadence环境下搭建了电路并进行了仿真，仿真结果如图6所示。可以看出各等级下波形的特征参数都符合IEC61000-4-2标准且具有较高的精确度。其中，第1峰值电流误差在2.8%以内，30 ns电流值误差在3.1%以内，60 ns电流值误差在2.5%以内。可见，此模型具有很好的精确性与稳定性，很适合用于接触放电仿真测试。

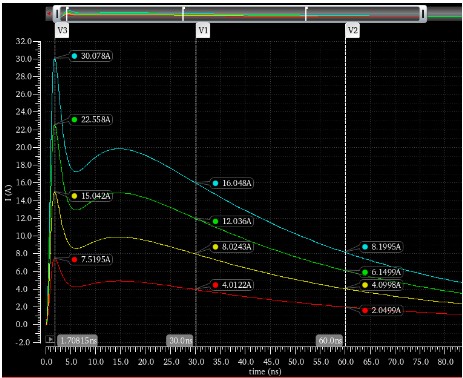
图6 Cadence下接触放电仿真波形图

3 HBM电路模型

为了扩展模型的实用性，把接触放电模型改成了HBM模型。图7为静电枪的HBM模型，它与接触放电模式的不同点在于：原电路中R1的阻值由330 Ω变成1.5 kΩ，C1的电容值由150 pF变为100 pF。2 kV下模型产生的放电电流波形如图8所示，其中红色线是Cadence下仿真曲线，蓝色线是实测曲线，可以看出两者的吻合度也是很好的。改进后的模型可用于静电仿真测试中的HBM测试。

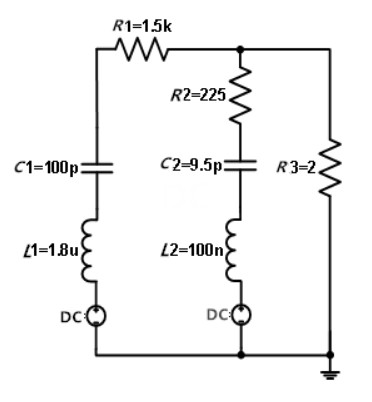
图7 HBM模型电路原理图

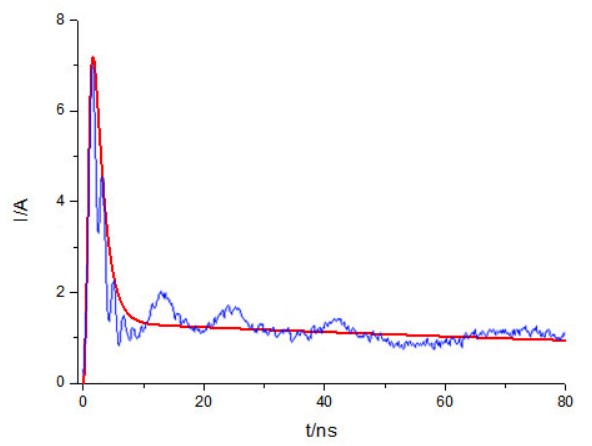
图8 2 kV下HBM模型的仿真与实测对比图

4 结论

本文提出了一种新的静电发生器电路模型，该模型在Cadence中建立并验证。优点是：①模型产生的波形很稳定且与实测波形的吻合度较好；②适用于2种测试模式，接触放电测试和HBM测试。其中，接触放电的仿真结果与IEC61000-4-2标准非常吻合。第1峰值电流误差在2.8%以内，30 ns电流值误差在3.1%以内，60 ns电流值误差在2.5%以内。此外，HBM模型的仿真结果与实测波形的吻合性也很好，从而证实了新模型系统行为的准确性。该电路模型为静电放电仿真提供了1个新的激励源。
责任编辑:tzh