图的逻辑结构是怎样的？如何去实现它？

经常有读者问我「图」这种数据结构，因为我们公众号什么数据结构和算法都写过了，唯独没有专门介绍「图」。

其实在学习数据结构和算法的框架思维中说过，虽然图可以玩出更多的算法，解决更复杂的问题，但本质上图可以认为是多叉树的延伸。

面试笔试很少出现图相关的问题，就算有，大多也是简单的遍历问题，基本上可以完全照搬多叉树的遍历。

至于最小生成树，Dijkstra，网络流这些算法问题，他们当然很牛逼，但是，就算法笔试来说，学习的成本高但收益低，没什么性价比，不如多刷几道动态规划，真的。

那么，本文依然秉持我们号的风格，只讲「图」最实用的，离我们最近的部分，让你心里对图有个直观的认识。

图的逻辑结构和具体实现

一幅图是由节点和边构成的，逻辑结构如下：

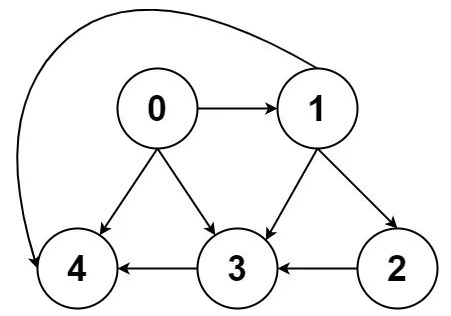
什么叫「逻辑结构」？就是说为了方便研究，我们把图抽象成这个样子。

根据这个逻辑结构，我们可以认为每个节点的实现如下：

/* 图节点的逻辑结构 */class Vertex {

int id;

Vertex［］ neighbors;

}

看到这个实现，你有没有很熟悉？它和我们之前说的多叉树节点几乎完全一样：

/* 基本的 N 叉树节点 */class TreeNode {

int val;

TreeNode［］ children;

}

所以说，图真的没啥高深的，就是高级点的多叉树而已。

不过呢，上面的这种实现是「逻辑上的」，实际上我们很少用这个Vertex类实现图，而是用常说的邻接表和邻接矩阵来实现。

比如还是刚才那幅图：

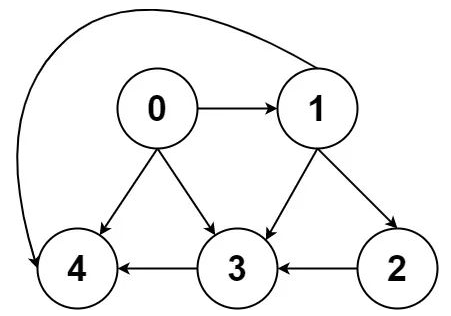
用邻接表和邻接矩阵的存储方式如下：

邻接表很直观，我把每个节点x的邻居都存到一个列表里，然后把x和这个列表关联起来，这样就可以通过一个节点x找到它的所有相邻节点。

邻接矩阵则是一个二维布尔数组，我们权且成为matrix，如果节点x和y是相连的，那么就把matrix［x］［y］设为true。如果想找节点x的邻居，去扫一圈matrix［x］［。。］就行了。

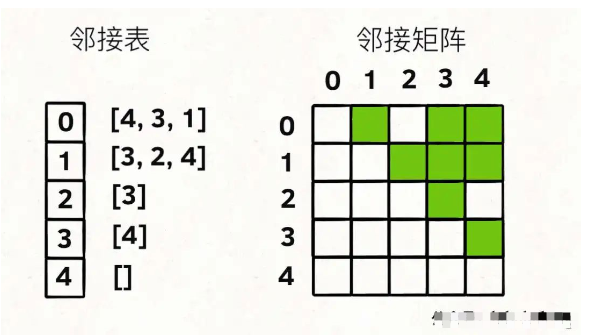
那么，为什么有这两种存储图的方式呢？肯定是因为他们各有优劣。

对于邻接表，好处是占用的空间少。

你看邻接矩阵里面空着那么多位置，肯定需要更多的存储空间。

但是，邻接表无法快速判断两个节点是否相邻。

比如说我想判断节点1是否和节点3相邻，我要去邻接表里1对应的邻居列表里查找3是否存在。但对于邻接矩阵就简单了，只要看看matrix［1］［3］就知道了，效率高。

所以说，使用哪一种方式实现图，要看具体情况。

好了，对于「图」这种数据结构，能看懂上面这些就绰绰够用了。

那你可能会问，我们这个图的模型仅仅是「有向无权图」，不是还有什么加权图，无向图，等等……

其实，这些更复杂的模型都是基于这个最简单的图衍生出来的。

有向加权图怎么实现？很简单呀：

如果是邻接表，我们不仅仅存储某个节点x的所有邻居节点，还存储x到每个邻居的权重，不就实现加权有向图了吗？

如果是邻接矩阵，matrix［x］［y］不再是布尔值，而是一个 int 值，0 表示没有连接，其他值表示权重，不就变成加权有向图了吗？

无向图怎么实现？也很简单，所谓的「无向」，是不是等同于「双向」？

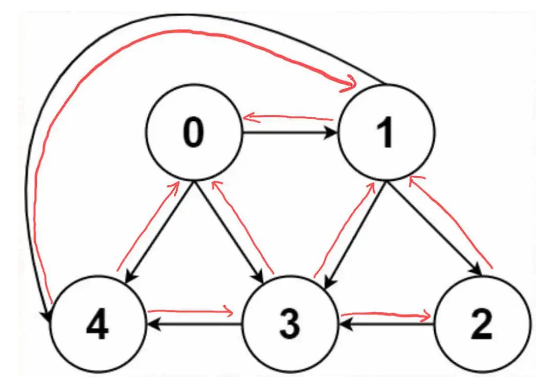
如果连接无向图中的节点x和y，把matrix［x］［y］和matrix［y］［x］都变成true不就行了；邻接表也是类似的操作。

把上面的技巧合起来，就变成了无向加权图……

好了，关于图的基本介绍就到这里，现在不管来什么乱七八糟的图，你心里应该都有底了。

下面来看看所有数据结构都逃不过的问题：遍历。

图的遍历

图怎么遍历？还是那句话，参考多叉树，多叉树的遍历框架如下：

/* 多叉树遍历框架 */void traverse（TreeNode root） {

if （root == null） return;

for （TreeNode child ： root.children）

traverse（child）;

}

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点。

所以，如果图包含环，遍历框架就要一个visited数组进行辅助：

Graph graph;

boolean［］ visited;

/* 图遍历框架 */void traverse（Graph graph， int s） {

if （visited［s］） return;

// 经过节点 s

visited［s］ = true;

for （TreeNode neighbor ： graph.neighbors（s））

traverse（neighbor）;

// 离开节点 s

visited［s］ = false;

}

好吧，看到这个框架，你是不是又想到了 回溯算法核心套路 中的回溯算法框架？

这个visited数组的操作很像回溯算法做「做选择」和「撤销选择」，区别在于位置，回溯算法的「做选择」和「撤销选择」在 for 循环里面，而对visited数组的操作在 for 循环外面。

在 for 循环里面和外面唯一的区别就是对根节点的处理。

比如下面两种多叉树的遍历：

void traverse（TreeNode root） {

if （root == null） return;

System.out.println（“enter： ” + root.val）;

for （TreeNode child ： root.children） {

traverse（child）;

}

System.out.println（“leave： ” + root.val）;

}

void traverse（TreeNode root） {

if （root == null） return;

for （TreeNode child ： root.children） {

System.out.println（“enter： ” + child.val）;

traverse（child）;

System.out.println（“leave： ” + child.val）;

}

}

前者会正确打印所有节点的进入和离开信息，而后者唯独会少打印整棵树根节点的进入和离开信息。

为什么回溯算法框架会用后者？因为回溯算法关注的不是节点，而是树枝，不信你看 回溯算法核心套路 里面的图，它可以忽略根节点。

显然，对于这里「图」的遍历，我们应该把visited的操作放到 for 循环外面，否则会漏掉起始点的遍历。

当然，当有向图含有环的时候才需要visited数组辅助，如果不含环，连visited数组都省了，基本就是多叉树的遍历。

题目实践

下面我们来看力扣第 797 题「所有可能路径」，函数签名如下：

List《List《Integer》》 allPathsSourceTarget（int［］［］ graph）;

题目输入一幅有向无环图，这个图包含n个节点，标号为0， 1， 2，。。。， n - 1，请你计算所有从节点0到节点n - 1的路径。

输入的这个graph其实就是「邻接表」表示的一幅图，graph［i］存储这节点i的所有邻居节点。

比如输入graph = ［［1，2］，［3］，［3］，［］］，就代表下面这幅图：

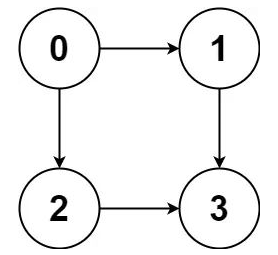
算法应该返回［［0，1，3］，［0，2，3］］，即0到3的所有路径。

解法很简单，以0为起点遍历图，同时记录遍历过的路径，当遍历到终点时将路径记录下来即可。

既然输入的图是无环的，我们就不需要visited数组辅助了，直接套用图的遍历框架：

// 记录所有路径

List《List《Integer》》 res = new LinkedList《》（）;

public List《List《Integer》》 allPathsSourceTarget（int［］［］ graph） {

LinkedList《Integer》 path = new LinkedList《》（）;

traverse（graph， 0， path）;

return res;

}

/* 图的遍历框架 */void traverse（int［］［］ graph， int s， LinkedList《Integer》 path） {

// 添加节点 s 到路径

path.addLast（s）;

int n = graph.length;

if （s == n - 1） {

// 到达终点

res.add（new LinkedList《》（path））;

path.removeLast（）;

return;

}

// 递归每个相邻节点

for （int v ： graph［s］） {

traverse（graph， v， path）;

}

// 从路径移出节点 s

path.removeLast（）;

}

这道题就这样解决了。

最后总结一下，图的存储方式主要有邻接表和邻接矩阵，无论什么花里胡哨的图，都可以用这两种方式存储。

在笔试中，最常考的算法是图的遍历，和多叉树的遍历框架是非常类似的。

当然，图还会有很多其他的有趣算法，比如二分图判定呀，环检测呀（编译器循环引用检测就是类似的算法）等等，以后有机会再讲吧，本文就到这了。

责任编辑：lq6