更精确电子结构的展示—新软件的作用

Wannier函数是评估固体材料中各种电子性质的有力工具，其应用范围涵盖电极化和轨道磁化以及拓扑性质等。此外，Wannier函数提供了一种通过紧凑的汉密尔顿方法，用以描述晶体中的能带，因此可以在不需要额外调用代码的情况下，快速评估布里渊区中任何一点的能带结构。

这种Wannier插值方法在原理上类似于紧束缚方法，但具有显著的优势。Wannier插值提供了一个系统方法，在不截断跳跃积分的情况下，可精确描述任何数量的能带，相比之下，传统的紧束缚方法因基组数量有限而不可避免地出现误差。此外，该方法还可以精确地插值能带的能量、各种观测值和算符的矩阵元。

这类插值在寻找能带结构中的外尔点、评估快速变化函数的动量空间积分时，都特别有用。这类积分包括反常霍尔电导、轨道磁化、玻耳兹曼输运系数和光学性质的计算等。

目前，已有多种Wannier插值方案，已用于需在布里渊区进行密集采样的性质计算中，如电子-声子耦合、陀螺效应和自旋霍尔电导等。然而，更复杂的物理问题和材料带来了更难的数值计算挑战，用现有的代码计算将变得非常昂贵，阻碍Wannier插值方法所能达到的预期精度。

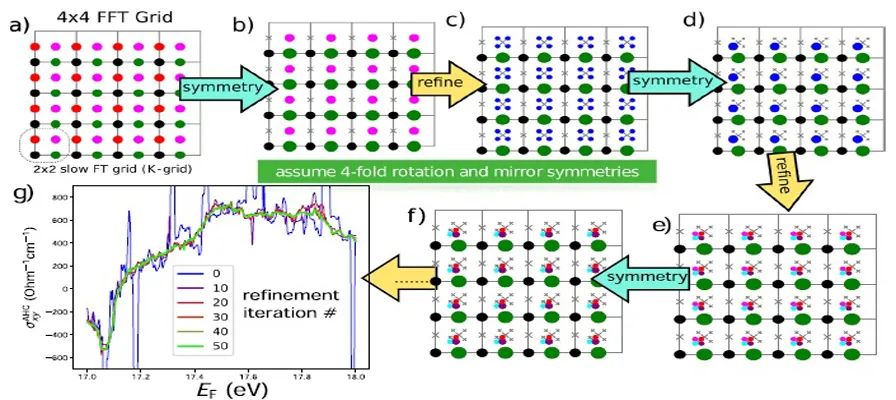
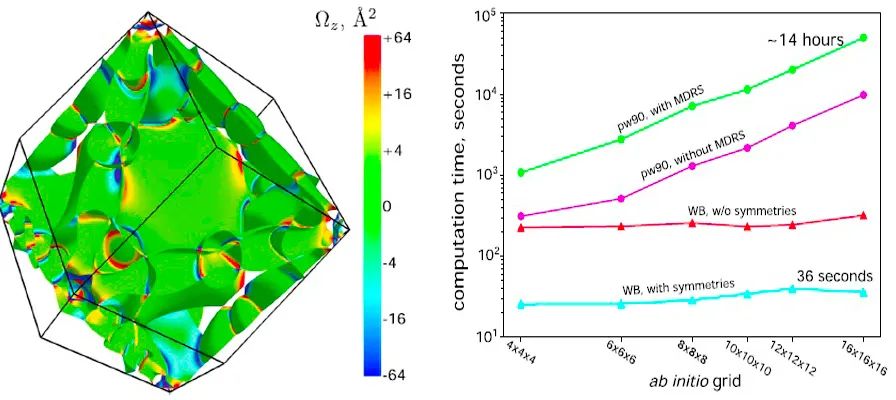
来自瑞士苏黎世大学物理系的Stepan S. Tsirkin教授提出了一系列方法，将Wannier插值的性能提升到了更高的水平。这些方法是在Python代码WannierBerri中实现的。混合并优化了傅里叶变换和最小距离复制选择法（MDRS），Fermi能级迭代不仅在计算上有很大优势，而且并不影响计算精度。

因此，WannierBerri可以很容易地用已建立的postw90.x代码进行基准测试。该代码不仅可以对反常霍尔电导率和其他属性作高速度和高精度的计算，还可以作为平台来实现更多Wannier插值的功能。因此，它有可能成为一个社区代码。有趣的是，该代码使用同一程序来执行基于Wannier函数和紧束缚模型的计算。

该文近期发表于npj Computational Materials 7： 33 （2021），英文标题与摘要如下。

High performance Wannier interpolation of Berry curvature and related quantities with Wannier Berri code

Stepan S. Tsirkin

Wannier interpolation is a powerful tool for performing Brillouin zone integrals over dense grids of k points， which are essential to evaluate such quantities as the intrinsic anomalous Hall conductivity or Boltzmann transport coefficients.

However， more complex physical problems and materials create harder numerical challenges， and computations with the existing codes become very expensive， which often prevents reaching the desired accuracy. In this article， I present a series of methods that boost the speed of Wannier interpolation by several orders of magnitude.

They include a combination of fast and slow Fourier transforms， explicit use of symmetries， and recursive adaptive grid refinement among others. The proposed methodology has been implemented in the python code WannierBerri， which also aims to serve as a convenient platform for the future development of interpolation schemes for other phenomena.

编辑：jq