浅析希尔伯特变换简介以及希尔伯特变换意义

1 hilbert变换

希尔伯特变换是以著名数学家大卫·希尔伯特（David Hilbert）来命名。在数学与信号处理的领域中，一个实值函数的希尔伯特变换（Hilbert transform）——在此标示为H——是将信号g（t）与1/（πt）做卷积，以得到g‘（t）。因此，希尔伯特变换结果g’（t）可以被解读为输入是g（t）的线性时不变系统（linear time invariant system）的输出，而此系统的脉冲响应为1/（πt）。

希尔伯特变换公式：

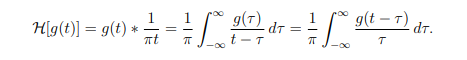
g（t） 的希尔伯特变换是 g（t） 与信号 1/πt 的卷积。 它是脉冲响应为 1/πt 的线性时不变滤波器（称为希尔伯特变换器）对 g（t） 的响应。 希尔伯特变换 H［g（t）］ 通常表示为 ˆg（t） 或 ［g（t）］∧。

傅立叶变换的相互作用

信号 1/（πt） 进行傅立叶变换：

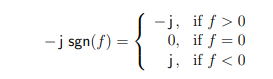
如果 g（t） 有傅里叶变换 G（f），那么，从傅里叶变换的卷积性质，可知 ˆg（t） 有傅里叶变换

希尔伯特实际上是一个使相位滞后pi/2的全通移相网络。

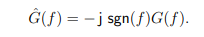
2 希尔伯特变换意义

首先，将实数信号变换成解析信号的结果就是，把一个一维的信号变成了二维复平面上的信号，复数的模和幅角代表了信号的幅度和相位。

这样看来，似乎复数信号才是完整的，而实信号只是在复平面的实轴上的一个投影。我们知道，解析信号可以计算包络（瞬时振幅）和瞬时相位。实际上我们计算的包络就是黑色的线围成的立体图形的边界在实部的投影。

而计算这个边的投影也很简单，就是在复平面上的螺旋线中的每一个点的模值，也就是A（t） = sqrt（x^2（t） + Hilbert（x（t））^2），而瞬时相位就是虚部（Hilbert变换后的）和实部（原始信号）在某一时间点的比值的arctan，瞬时频率就是它的导数。

3 matlab 希尔伯特变换

Hilbert 变换可用于形成解析信号。解析信号在通信领域中很有用，尤其是在带通信号处理中。工具箱函数 hilbert 计算实数输入序列 x 的 Hilbert 变换，并返回相同长度的复数结果，即 y = hilbert（x），其中 y 的实部是原始实数数据，虚部是实际 Hilbert 变换。在涉及到连续时间解析信号时，y 有时被称为解析信号。离散时间解析信号的关键属性是它的 Z 变换在单位圆的下半部分为 0。解析信号的许多应用都与此属性相关；例如，用解析信号避免带通采样操作的混叠效应。解析信号的幅值是原始信号的复包络。

Hilbert 变换对实际数据作 90 度相移；正弦变为余弦，反之亦然。

close allclear allclc Fs =44100;%44.1khz fc =1000; %1khzN=8192;t=0：（100/Fs）：10; x=sin（2*pi*t）;y=hilbert（x）; figure（1），hold onplot（t，real（y），‘red’）;plot（t，imag（y））;hold offaxis（［0 10 -1.1 1.1］）legend（‘Real’，‘imaginary’）

编辑：jq