适用于分布式MIMO系统中的时间频率同步算法研究

MIMO技术近年来得到了很多学者和研究机构的重视，但是它要求信道平衰落的前提条件限制了它在宽带无线通信中的应用，为了避免符号间干扰，通常需要在接收端加信道均衡器。由于有很多根收发天线，这种均衡器是非常复杂的。另一种解决方法是将OFDM技术与MIMO技术结合起来，利用OFDM技术对多径的对抗能力，去除符号间干扰，实现宽带高速无线通信。但MIMO-OFDM系统对同步误差很敏感：在多径环境下， MIMO-OFDM系统对时间同步的要求很高；频率同步方面，由于MIMO-OFDM系统可以视为N个并行的MIMO子系统，因此频偏所引入的ICI会恶化每个子载波的信噪比，从而恶化整个MIMO-OFDM通信系统的传输性能。

对MIMO-OFDM系统来说，时间同步方面，接收端需要对各个天线上的信号分别进行延时估计和调整。频率同步方面，接收端需要对各个天线上的信号分别进行频率偏移估计和补偿。传统的MIMO-OFDM同步算法，未能完全解决这种情况下的同步问题。这种新的适用于 MIMO-OFDM系统的时间频率同步算法考虑了各发射天线到达时延各不相同的情况，因此具有更广泛意义，可适用于分布式MIMO系统。

1、MIMO-OFDM技术概述

对MIMO-OFDM技术来说，其核心部分是OFDM技术和MIMO技术。OFDM通过将频率选择性多径衰落信道在频域内转换为平坦信道，从而减少了多径衰落的影响。而MIMO技术能够在空间中产生独立的并行信道同时传输多路数据流，这样就有效地增加了系统的传输速率。这样，OFDM和MIMO两种技术的结合，就能达到两种效果：一种是系统具备很高的传输速率，另一种是通过分集达到很强的可靠性。

2、MIMO-OFDM同步技术研究现状

在MIMO系统中，由于发射天线的增加导致发射信号不但要受到与传统单天线系统中相同的各种干扰的影响，而且还存在天线间干扰。因此MIMO- OFDM系统中的同步问题比单天线系统中要困难得多，许多用于单天线系统的同步方法不能直接应用于MIMO-OFDM系统。目前对MIMO-OFDM系统同步的研究还刚刚开始，公开发表的文献还不多，其中既有研究集中式MIMO的，也有研究分布式MIMO的，但研究集中式MIMO的居多，而且在分布式 MIMO中大都是研究频率同步的，没有研究时间同步，都假设时间同步已经完成，而且各天线对之间的时延均相同。

3、新的MIMO-OFDM同步算法

3.1系统设计

算法框图如图1所示。

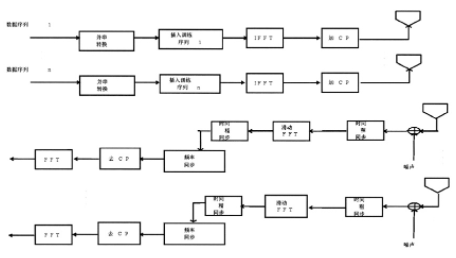
图1MIMO-OFDM系统结构图

假设一个MIMO-OFDM系统有N个子载波，M个发射天线，P个接收天线，定义第m个发射天线上的OFDM调制信号为：

这里△表示多径信道的径数，hlmp表示第mp个MIMO子信道中第l径的衰落系数。Sl表示MIMO子信道中第l径的时延。dm表示接收天线收到各路发射天线信号的相对时延。这里定义第一路发射天线的相对时延是零。Np（t）是第p路接收天线上的加性噪声，设

Dp=max{d1，d2，…，dm}。

这种新的时间同步算法适用于各路天线到达时延不同的情况。传统的MIMO-OFDM系统同步算法并不能解决当各路天线到达时延不同时的同步问题。针对这种情况，我们提出了新的导引符号配置方法：第一，频域各天线的训练序列分开放置，用来区分不同时延，可以进行时间精同步；第二，在接收端时域，这些分开放置的训练序列又具有相同的两个半段，可以用来做时间粗同步和频率粗同步。

在发射端的频域，如果训练序列的齐位插入伪随机序列，偶位插入零，那么经过IFFT之后就可以得到前后两个相同的半段序列。于是我们的训练序列的插入方法如下，该方法可以保证M条发射天线上的训练序列经过IFFT之后，都可以得到两个相同的半段序列。因此即使当各个发射天线到达接收天线的时延不同时，接收天线依然可以得到两段相同的序列。

定义每个天线发射的训练序列为Tm（i），其中插入的伪随机序列为Cm（k），长度为Q，这里总的子载波数N和发射天线数M间必须满足：N=2MQ，第m个发射天线插入练序列的方式为

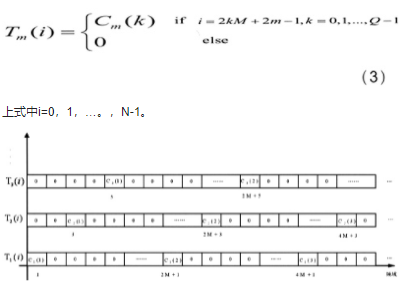
图2训练序列插入方式

如图2所示，这样插入就保证了每路发射天线的训练序列都是在偶位全为零，奇位则为伪随机序列和零，可以保证在IFFT之后，每路天线的导引在时域都对称，这样在时延不同的情况下叠加，都可以得到两个相同的半段序列。

设tm（i）是对应的Tm（i）经过IFFT之后的结果：

如图3所示，假设ai，bi，ci分别是t1（i），t2（i），t3（i）的序列。d2，d3分别是t2（i），t3（i）序列相对于t1（i）的延迟。当d3为最大延迟时，按照图中的方式叠加后，两个半段序列1和2是完全相同的。

图3时域上各路有延迟的序列叠加

3.2时间同步

3.2.1粗同步

首先在接收端建立一个长度为N的滑动窗，按照我们提出的训练序列插入方式，当处于正确的时间点时，在滑动窗中的训练序列就是两个相同的前后部分。

考虑到M路天线相对延迟不同，所以前后两个半段有Dp长度部分不同。于是我们可以定义时间粗同步公式为：

上面的计算，因为除掉了上面提到的小部分的不同，所以在训练序列正好对齐的时候就可以得到一个归一化的峰值。

然后设置一个硬判门限和搜索长度L，将从M（d）超过门限的滑动窗中的那段序列开始，连续将L个长度为N的序列送入后续的精同步部分处理，并且记录超过门限的时间点为。设这段序列为gi（t），i=0，1，…，L-1，t=0，1，…。，N-1。

3.2.2精同步

得到了L个长度为N的序列，将他们分别进行FFT运算：

上式中，i=0，1，…，L-1，k=0，1，…。，N-1。

然后将Gi（k）按照先前插训练序列的方式，将其中的伪随机序列抽取出来，和本地序列进行相关相乘，就可以得到第m路发射天线信号的时间精同步点了：

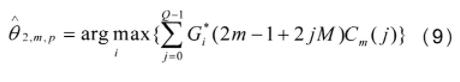
上式中，m=1，2，…。，M。

因为有m个发射天线，因此公式（9）要进行m次运算，确定每个发射天线到第p个接收天线的时间精同步点。

所以，得到第m路发射天线信号到达第p路接收天线的时间同步点：

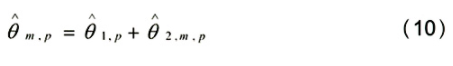
3.3频率同步

在时间同步后实现频率同步。这里我们仍然可以利用在时域得到的两个相同的半段训练来进行频率偏移估计，与时间粗同步一样，也要除去两个半段序列中τ长度部分的序列，假定各路发射天线的时间同步点中，的相对延迟为零。于是得到频偏估计：

3.4数据与仿真结果

设MIMO系统为四发四收和两发两收结构，子载波数为N=2048，带宽是20 MHz，信道是COST207六径rayleigh信道，各径时延以40个采样点递增，功率以6 dB递减，速率为70 km/h。四个发射天线到达接收天线的时延分别为0，5，10，15个采样点，因此我们令τ为20个采样点，来进行时间和频率同步。频偏设为0.4，时间精同步搜索长度L=250。由于进行时间粗同步时，得到的峰值会受到噪声的影响，因此硬判值在不同信噪比条件下并不相同，一般来说，是随信噪比的升高呈递增趋势。仿真数据长度是10万帧。

如图4所示。在信噪比较低的情况下，两种情况下时间同步的错误率比较高，并且随着信噪比的升高而逐渐降低，在10 dB的时候错误率降低幅度很大。在12，14 dB的时候错误率几乎为零。说明新算法在各路发射天线时延不同情况下，仍然可以得到良好的时间同步性能。

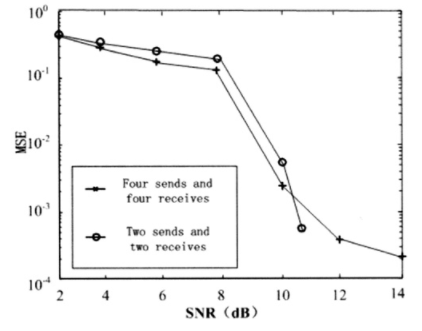
图4新算法的时间同步性能曲线

如图5所示。两种情况下频率同步的MSE值随着信噪比的升高而逐渐降低，四发四收和两发两收情况得到的MSE值很接近，说明频率同步算法可以得到和Schmidl算法同样的频率同步性能。

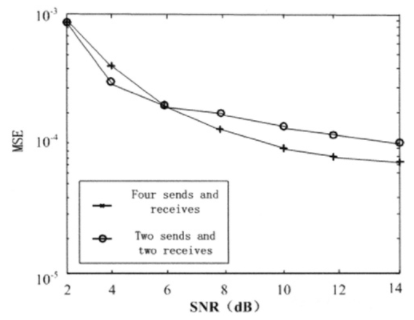
图5新算法的频率同步性能曲线

通过以上仿真可以看到，该算法在多径环境下可以得到良好的同步性能。

4、结束语

目前，世界各国和各大电信厂商都已经展开了新一代移动通信系统的研究，而且由于MIMO-OFDM在提高无线链路的传输速率和可靠性的巨大潜力，使得这两种技术的结合有望成为过渡到4G的潜在技术。因此MIMO-OFDM已经成为目前4G研究的热点。本文提出的新的 MIMO-OFDM同步方法设置了新的导引符号配置方法，可以在接收端时域得到相同的两个半段序列，进行时间粗同步和频率同步，频域再根据导引插入规则进行时间精同步。仿真结果表明，该方法能实现对多个发射天线时间延迟估计，可适用于分布式MIMO系统。

责任编辑：gt