教大家怎么选择神经网络的超参数

1. 神经网络的超参数分类

神经网路中的超参数主要包括：

学习率 η，

正则化参数 λ，

神经网络的层数 L，

每一个隐层中神经元的个数 j ，

学习的回合数Epoch，

小批量数据 minibatch 的大小，

输出神经元的编码方式，

代价函数的选择，

权重初始化的方法，

神经元激活函数的种类，

参加训练模型数据的规模

这些都是可以影响神经网络学习速度和最后分类结果，其中神经网络的学习速度主要根据训练集上代价函数下降的快慢有关，而最后的分类的结果主要跟在验证集上的分类正确率有关。因此可以根据该参数主要影响代价函数还是影响分类正确率进行分类。

在上图中可以看到超参数 2，3，4，7 主要影响的是神经网络的分类正确率；9主要影响代价函数曲线下降速度，同时有时也会影响正确率；1，8，10 主要影响学习速度，这点主要体现在训练数据代价函数曲线的下降速度上；

5，6，11 主要影响模型分类正确率和训练用总体时间。这上面所提到的是某个超参数对于神经网络想到的首要影响，并不代表着该超参数只影响学习速度或者正确率。因为不同的超参数的类别不同，因此在调整超参数的时候也应该根据对应超参数的类别进行调整。在调整超参数的过程中有根据机理选择超参数的方法，有根据训练集上表现情况选择超参数的方法，也有根据验证集上训练数据选择超参数的方法。他们之间的关系如图2所示。

超参数 7，8，9，10 由神经网络的机理进行选择。在这四个参数中，应该首先对第10个参数神经元的种类进行选择，根据目前的知识，一种较好的选择方式是对于神经网络的隐层采用sigmoid神经元，而对于输出层采用softmax的方法；

根据输出层采用sotmax的方法，因此第8个代价函数采用 log-likelihood 函数（或者输出层还是正常的sigmoid神经元而代价函数为交叉熵函数），第9个初始化权重采用均值为0方差为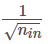的高斯随机分布初始化权重；对于输出层的编码方式常常采用向量式的编码方式，基本上不会使用实际的数值或者二进制的编码方式。

超参数1由训练数据的代价函数选择，在上述这两部分都确定好之后在根据检验集数据确定最后的几个超参数。这只是一个大体的思路，具体每一个参数的确定将在下面具体介绍。

2. 宽泛策略

根据上面的分析我们已经根据机理将神经网络中的神经元的种类、输出层的模式（即是否采用softmax）、代价函数及输出层的编码方式进行了设定。所以在这四个超参数被确定了之后变需要确定其他的超参数了。

假设我们是从头开始训练一个神经网络的，我们对于其他参数的取值本身没有任何经验，所以不可能一上来就训练一个很复杂的神经网络，这时就要采用宽泛策略。宽泛策略的核心在于简化和监控。简化具体体现在，如简化我们的问题，如将一个10分类问题转变为一个2分类问题；简化网络的结构，如从一个仅包含10个神经元的隐层开始训练，逐渐增加网络的层数和神经元的个数；

简化训练用的数据，在简化问题中，我们已经减少了80%的数据量，在这里我们该要精简检验集中数据的数量，因为真正验证的是网络的性能，所以仅用少量的验证集数据也是可以的，如仅采用100个验证集数据。

监控具体指的是提高监控的频率，比如说原来是每5000次训练返回一次代价函数或者分类正确率，现在每1000次训练就返回一次。其实可以将“宽泛策略”当作是一种对于网络的简单初始化和一种监控策略，这样可以更加快速地实验其他的超参数，或者甚至接近同步地进行不同参数的组合的评比。

直觉上看，这看起来简化问题和架构仅仅会降低你的效率。实际上，这样能够将进度加快，因为你能够更快地找到传达出有意义的信号的网络。一旦你获得这些信号，你可以尝尝通过微调超参数获得快速的性能提升。

3. 学习率的调整

假设我们运行了三个不同学习速率（ η=0.025、η=0.25、η=2.5）的 MNIST 网 络，其他的超参数假设已经设置为进行30回合，minibatch 大小为10，然后 λ=5.0，使用50000幅训练图像，训练代价的变化情况如图3

使用 η=0.025 ，代价函数平滑下降到最后的回合；使用 η=0.25 ，代价刚开始下降，在大约 20 回合后接近饱和状态，后面就是微小的震荡和随机抖动；最终使用 η=2.5 代价从始至终都震荡得非常明显。

因此学习率的调整步骤为：首先，我们选择在训练数据上的代价立即开始下降而非震荡或者增加时的作为 η 阈值的估计，不需要太过精确，确定量级即可。如果代价在训练的前面若干回合开始下降，你就可以逐步增加 η 的量级，直到你找到一个的值使得在开始若干回合代价就开始震荡或者增加；

相反，如果代价函数曲线开始震荡或者增加，那就尝试减小量级直到你找到代价在开始回合就下降的设定，取阈值的一半就确定了学习速率 。在这里使用训练数据的原因是学习速率主要的目的是控制梯度下降的步长，监控训练代价是最好的检测步长过大的方法。

4. 迭代次数

提前停止表示在每个回合的最后，我们都要计算验证集上的分类准确率，当准确率不再提升，就终止它也就确定了迭代次数（或者称回合数）。另外，提前停止也能够帮助我们避免过度拟合。

我们需要再明确一下什么叫做分类准确率不再提升，这样方可实现提前停止。正如我们已经看到的，分类准确率在整体趋势下降的时候仍旧会抖动或者震荡。如果我们在准确度刚开始下降的时候就停止，那么肯定会错过更好的选择。

一种不错的解决方案是如果分类准确率在一段时间内不再提升的时候终止。建议在更加深入地理解 网络训练的方式时，仅仅在初始阶段使用 10 回合不提升规则，然后逐步地选择更久的回合，比如 20 回合不提升就终止，30 回合不提升就终止，以此类推。

5. 正则化参数

我建议，开始时代价函数不包含正则项，只是先确定 η 的值。使用确定出来的 η ，用验证数据来选择好的 λ 。尝试从 λ=1 开始，然后根据验证集上的性能按照因子 10 增加或减少其值。一旦我已经找到一个好的量级，你可以改进 λ 的值。这里搞定 λ 后，你就可以返回再重新优化 η 。

6. 小批量数据的大小

选择最好的小批量数据大小也是一种折衷。太小了，你不会用上很好的矩阵库的快速计算；太大，你是不能够足够频繁地更新权重的。你所需要的是选择一个折中的值，可以最大化学习的速度。幸运的是，小批量数据大小的选择其实是相对独立的一个超参数（网络整体架构外的参数），所以你不需要优化那些参数来寻找好的小批量数据大小。

因此，可以选择的方式就是使用某些可以接受的值（不需要是最优的）作为其他参数的选择，然后进行不同小批量数据大小的尝试，像上面那样调整 η 。画出验证准确率的值随时间（非回合）变化的图，选择哪个得到最快性能的提升的小批量数据大小。得到了小批量数据大小，也就可以对其他的超参数进行优化了。

7. 总体的调参过程

首先应该根据机理确定激活函数的种类，之后确定代价函数种类和权重初始化的方法，以及输出层的编码方式；其次根据“宽泛策略”先大致搭建一个简单的结构，确定神经网络中隐层的数目以及每一个隐层中神经元的个数；

然后对于剩下的超参数先随机给一个可能的值，在代价函数中先不考虑正则项的存在，调整学习率得到一个较为合适的学习率的阈值，取阈值的一半作为调整学习率过程中的初始值 ；

之后通过实验确定minibatch的大小；之后仔细调整学习率，使用确定出来的 η ，用验证数据来选择好的 λ ，搞定 λ 后，你就可以返回再重新优化 η 。而学习回合数可以通过上述这些实验进行一个整体的观察再确定。

版权声明：本文为CSDN博主「独孤呆博」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/dugudaibo/article/details/77366245

编辑：jq