从傅里叶变换如何推换出拉普拉斯变换？

从傅里叶级数、傅里叶变换推出拉普拉斯变换。拉普拉斯变换，这是一个非常有用的工具，建立了时域与复频域之间的联系，它将时域内的微分与积分的运算转换为乘法与除法的运算，它将微分方程转换成代数方程，使求解过程更加方便。

一、傅里叶变换的不足

傅里叶变换是非常有用的。因为它将时域中的激励用频域中无穷多个正弦分量来表示，使我们能用系统对正弦激励的稳态响应之和来讨论系统对非正弦激励的响应，从而使瞬变过程问题的求解得到简化。

特别是有关信号的分析与处理方面，诸如有关谐波成分、频率响应、系统带宽、波形失真等问题上，它都能给出物理意义清楚的结果。

但它也有不足之处。

首先，它只能处理符合狄利赫利条件的信号，而在实际中有许多重要的信号是不符合绝对可积可积条件的，即积分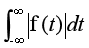不存在，如常见的阶跃信号U（t）；阶跃正弦信号sinωtU（t）等等。这样傅里叶变换法的适用范围就有一定的限制。

补充：

傅里叶级数分析使用的条件：傅里叶在提出傅里叶级数时坚持认为，任何一个周期信号都可以展开成傅里叶级数，虽然这个结论在当时引起许多争议，但持异议者却不能给出有力的不同论据。直到20年后（1829年）狄里赫利才对这个问题作出了令人信服的回答，狄里赫利认为，只有在满足一定条件时，周期信号才能展开成傅里叶级数。这个条件被称为狄里赫利条件，其内容为：

⑴ 在一个周期内，周期信号 x（t） 必须绝对可积；

⑵ 在一个周期内，周期信号 x（t） 只能有有限个极大值和极小值；

⑶ 在一个周期内，周期信号 x（t） 只能有有限个不连续点，而且，在这些不连续点上， x（t） 的函数值必须是有限值。

齐次，是在求取时域中的响应时，利用傅里叶反变换要进行对频域自负无穷大到正无穷大的无限积分，通常这个积分的求解是比较困难的。

二、频域中的傅里叶变换推广到复频域——拉普拉斯变换

将通过把频域中的傅里叶变换推广到复频域来解决这两个问题。

一个函数f（t）不满足绝对可积条件往往是由于在t趋于正无穷大或负无穷大的过程中减幅太慢的缘故。

如果用一个被称为收敛因子的指数函数e-σt去乘f（t），且δ取足够大的正值，则在时间的正方向上总可以使t→∞时，e-σtf（t）减幅较快。当然，这在时间负方向上反而将起增幅的作用。然而假使原来的函数在时间的负方向上是衰减的，而且其衰减速率较收敛因子引起的增长更快，则仍可以使得当t→-∞，f（t）e-σt也是减幅的。

例如下面的函数，在t的正方向上为一单位阶跃函数，在t的负方向上为一指数衰减函数，即

上式不难看出，只要σ《β，则函数f（t）e-σt在时间的正、负方向上将都是减幅的。即函数满足绝对可积的条件，可以进行傅里叶变换。

式（1）及式（2）组成了一对新的变换式子，称之为广义的傅里叶变换式或双边拉普拉斯变换式。

其中前者称为双边拉普拉斯正变换式，后者称为双边拉普拉斯反变换式；

F（s）称为f（t）的象函数，f（t）称为F（s）的原函数。

双边拉普拉斯变换式可用下列符号表示：

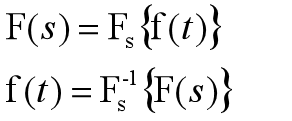
在实际应用中所遇到的激励信号与系统响应大都为有始函数，在有始函数的情况下，式（1）及（2）可以简化。因为有始函数在t《0范围内函数值为零，式（1）的积分在-∞到0的区间中为零，因此积分区间变为由0到∞，亦即

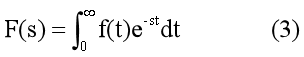
应该指出的是，为了适应激励与响应中在原点出现冲激函数或其各阶导数的情况，积分区间应包括零点在内，即式（3）中的积分下限应为0-。为了书写方便，今后仍写为0，但其意义表示0-。

至于式（2），则由于F（s）中包含的分量仍为由ω等于-∞到+∞的各个分量，所以其积分区间不变。但因为原函数为有始函数，故由式（2）求得的f（t），在t《0范围内必然为零。因此对有始函数来说式（2）可写为：

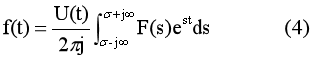
式（3）及式（4）也是一组变换对。因为现在只是对在时间轴一个方向上的函数进行变换，为区别于双边拉普拉斯变换式，故称之为单边拉普拉斯变换式，并标记如下：

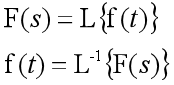
由以上分析可以看出，无论是双边或单边拉普拉斯变换都是傅里叶变换在复变数域中的推广。从物理意义上说，傅里叶变换是把函数分解成许多形式为函数ejωt的分量之和。每一对正负ω分量组成了一个等幅的正弦振荡。于此相类似，双边或单边拉普拉斯变换也是把函数分解成许多形式为函数est的指数分量之和。

通常称s为复频率，并可把F（s）看成是信号的复频谱。但严格说来，将s称为复频率是不太确切的，因为通常频率是指函数每秒内通过某定值（例如零值）的次数。而现在象函数包含的分量中存在有这样的分量

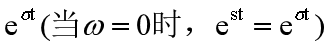
它是单调变化的，无频率可言。所以较为确切的说法应该是每一分量的频率由其s值的虚部决定。

责任编辑：lq6