近年来,随着无线技术的发展,对室内外环境中人员和物体的追踪定位引起了研究者的广泛研究,基于位置服务(LBS)越来越受到人们的关注。位置服务即根据服务消费者所在地理位置的不同提供对应的信息服务,作为LBS的核心技术之一,室内定位是其重要的组成部分。因为可以广泛用于室内路由、治安、消防等方面,因此定位算法的研究具有重要意义。在室内定位系统开发研究方面,常用的方法是在室内环境下建立小范围定位网络。目前,越来越多的定位直接利用现成的无线通讯模块来估计对象节点(盲节点)的位置,应运而生的ZigBee技术以低成本、低功耗成为室内定位的首选。本文以ZigBee组建基本的网络,通过节点接收RSSI值的大小来进行距离计算,最终通过距离以及参考节点的位置来计算定位节点(盲节点)位置。
1 无线网络定位技术
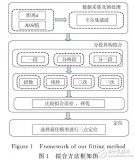
在无线定位中,有基于测距和非测距两种方式。前者需要测量相邻节点间的绝对距离或方位,并利用节点间的实际距离来计算未知节点的位置;后者无需测量节点的绝对距离或方位,而是利用节点间的估计距离计算节点位置。基于测距的算法主要包含以下几种:三边测量、三角测量、极大似然估计等;基于非测距的算法主要有质心算法、DV-Hop算法、D_distance算法、凸规划算法等。对定位算法的性能评价指标主要有定位精度、节点密度、容错和自适应性、功耗和代价、网络规模等几个部分。综合以上因素以及结合现有的设备,本文选用基于RSSI测距的定位方式。其流程图如图1所示。
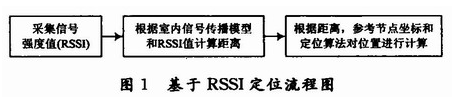
从图1可以看出定位由两部分组成:一是通过RSSI测距;二是根据距离以及参考节点位置计算盲节点位置。
2 RSSI测距模型
2.1 模型确立
无线信号传输中普遍采用的理论模型为Shadowing模型。该模型为:
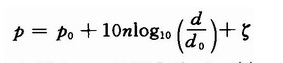
式中:do是参考距离;po是距离为do时接收到的信号强度,其中还包含了遮蔽外衰减或环境造成的损耗参考(中值);d是真实距离;ζ是以dB为单位的遮蔽因子,其均值为O,均方差为σdb(dB)正态随机变量;p是接收信号强度;n是路径损耗指数,它的值依赖于环境和建筑物的类型。在实际测量中,选用以下的模型:
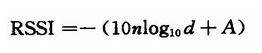
即不统计遮挡因子对RSSI的影响,在实际环境下对RSSI影响最大的是非视距的影响。其中,射频参数A被定义为用dBm表示的距离发射器1 m接收到的平均能量绝对值,也就是距发射节点1 m处的接收信号强度;n为信号传输常数,与信号传输环境有关;d为距发射节点的距离。
2.2 参数优化
在使用A和n进行距离计算时,首先要面临的一个问题是A和n的取值问题。A和n的取值不同,对测距的误差影响很大。为了使模型能够尽量真实地反映出当前室内环境中的传播特性,保证RSSI测距的精度,需要对A和n进行优化,得到最适合该室内环境情况的参数值。
通过线性回归分析来估计参数A和n的值,假设从室内环境得到的实验测量数据为(RSSIi,di),i=1,2,…,n,RSSIi表示在距离di上所对应的RSSI测量值。
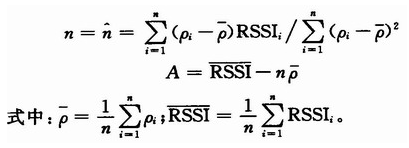
以实验室走廊为例,测得100组数据,代入上述公式得出A=4l,n=2.3。图2是参数优化后的RSSI测距模型曲线。在图中可以看出,根据线性回归分析可以很好地拟合出适应当前环境的模型曲线。
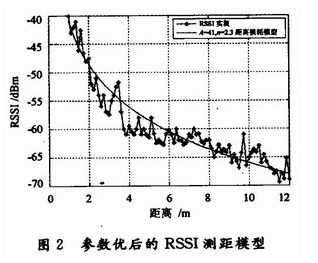
2.3 RSSI滤波处理
信号强度的定位算法中信号强度值随环境的改变有很高的灵敏度,这会限制测量的准确度。事实上信号强度与距离之间的关系很不让人满意,在环境中存在很大的波动性。在室内环境下实测得到的RSSI与节点间距离的关系曲线如图2所示。当传输距离较近的时候,RSSI值衰减得较快;当传输距离越远,衰减得越慢,接收强度对传输距离的变化表现不明显。在实际中,某一时间段内接收节点可以收到n个RSSI值,由于非视距和多径的影响,导致这些RSSI值具有很大的波动性,在代入公式进行计算之前,先进行滤波处理,得到一个比较准确的值,然后再进行计算。
本文采用高斯滤波模型进行RSSI滤波。引入高斯模型进行处理的原则是:在自然现象和社会现象中,大量随机变量都服从或近似正态分布,如材料性能、零件尺寸、化学成分、测量误差、人体高度等。
高概率发生区,选择概率大于O.6(O.6的取值是根据工程中的经验值)的范围。经过高斯滤波后,RSSI的取值范围为[0.15σ+μ,3.09 σ+μ]。其中:
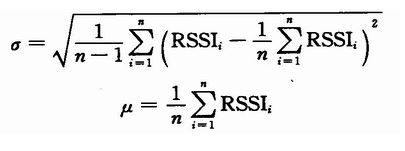
把该范围内的RSSI值全部取出,再求几何平均值,即可得到最终的RSSI值。
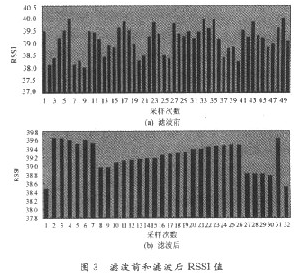
在d=1 m处,采集50组RSSI值,进行高斯滤波处理。
如图3所示,滤波前RSSI波动比较大,滤波后比较平滑。滤波前|RSSI|的平均值为38.9,计算距离d=O.71 m;滤波后|RSSI|的平均值为39.42,计算距离d=O.81 m。显然,高斯滤波能很好地提高测距精度。
3 定位算法
假设无线定位网络中有N个已知位置的参考节点,坐标为(x1,y1),(x2,y2),…,(xN,yN),RSSI测量值为(RSSI1,RSSI2,…,RSSIN)。通过利用无线信号传播衰落模型计算得到待定位节点到四个已知位置的参考节点的距离为R1,R2,…,RN,则可以得到以下方程:
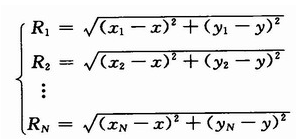
最终定位算法的研究就是求解该方程。在求解(x,y)过程中,选用基于泰勒级数展开迭代法进行计算。选用泰勒级数的原因基于以下几个方面:
(1)无需提供测距差测量值误差的先验信息。
(2)可以应用于两个以上数目距离差测量的定位估计。
(3)对距离差统计没有特殊要求。
(4)在适当的距离差噪声水平上提供较准确的定位估计。
使用泰勒级数进行定位计算,首先面临的一个问题即泰勒级数展开需要一个与实际位置差距不大的初始值,初始值的选择越接近真实值,越可以保证算法的收敛性以及实时性。本文采用极大似然估计法来获取初始值,求得初始值公式为:
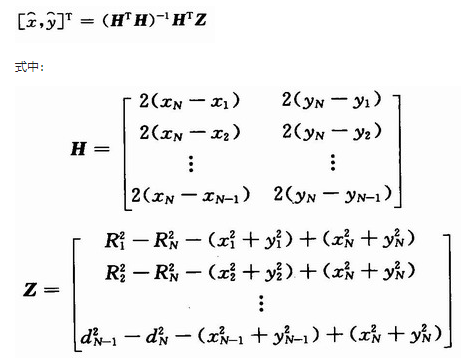
根据取得的值作为Taylor级数展开的循环初值,然后用Taylor级数展开,进行矩阵计算,并反复迭代求精,直到误差满足预先设定的门限,得出最终的位置坐标。
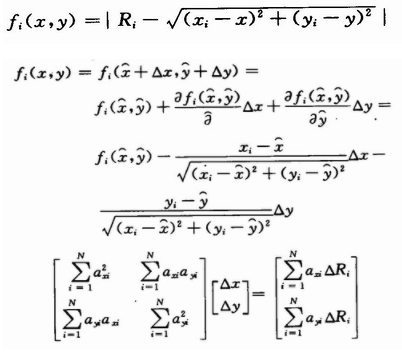
式中:

,重复以上过程,直到△x,△y足够小,满足一预先设定的门限ε,即(△x+△y)<ε,此时的(x,y)即为定位节点的估计位置。
4 实验验证
实验是在实验室走廊(4 m×30 m)进行的,实验环境如图4所示。选用的是ZigBee硬件平台作为通信平台,该平台CC2431自带定位引擎,可以实现位置估计,并通过实验比较两种算法的差异。
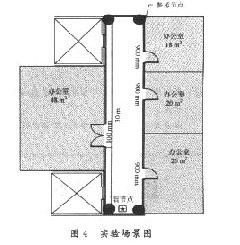
CC2431使用的三边测量法进行位置计算,采用均值滤波对RSSI进行滤波处理。ZigBee开发平台如图5所示。

在实验环境中布置4个节点作为参考节点,位置分别定义为(O,0),(0,4),(30,O),(30,4)。确定A和n的值,实验环境与图2的实验一样。可以得知,A=41,n=2.3。在环境中任取31个点,分别测得该点的实际位置(x,y);使用CC2431得到的位置(x’,y’),使用本文提
出的算法得到位置(x“,y”)。比较两个位置的误差大小d‘与d“,如图6所示。
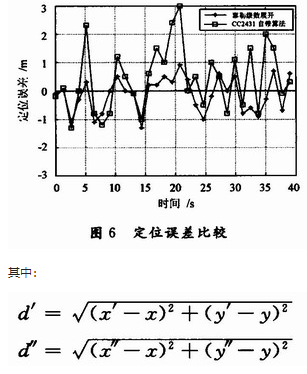
由图6可以看出,经过线性回归分析和高斯滤波,然后用泰勒级数展开,最终求得位置误差大约在1 m左右,而CC2431的定位误差在2~3 m左右。本文提出的定位算法较好地改善了定位效果,使定位误差主要集中在1 m左右,基本能够满足室内定位对误差的要求,提高了定位精度。
5 结语
对基于RSSI的室内定位算法以及RSSI测距进行了全面分析。通过线性回归分析对参数进行优化,高斯模型对RSSI进行滤波,提高了测距的精度。最后采用泰勒级数展开法进行位置计算,比较了CC2431的定位算法,减小了定位误差,达到了提高定位精度的目的,证实了定位算法的优越性。
责任编辑:gt
-
无线
+关注
关注
31文章
5450浏览量
173240 -
ZigBee
+关注
关注
158文章
2270浏览量
242730
发布评论请先 登录
相关推荐
基于rssi 指纹识别 室内定位
基于RSSI的定位技术进行了研究
RSSI信号的滤波分析(均值滤波、高斯滤波)

自适应的RSSI分段异构拟合定位方法
基于自适应动态测距的室内定位算法
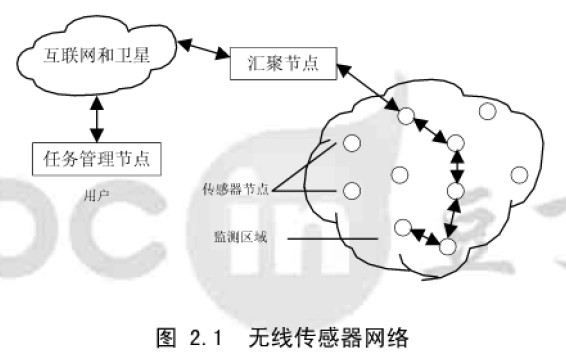
如何使用RSSI的无线传感器网络进行定位算法的设计与实现
蓝牙信标RSSI定位原理

主动式蓝牙RSSI定位系统和被动式蓝牙RSSI定位系统的原理




 基于RSSI的室内定位算法及RSSI测距的研究分析
基于RSSI的室内定位算法及RSSI测距的研究分析










评论