LC阻尼振荡莫不是有什么问题？

前两期说了RCD电路，不可避免提到开关的尖峰。由此我想到了我们最常用的电路，Buck电路。

Buck振荡波形

Buck电路电感前面的SW波形，想必大家都测量过，总的来说，无非下面两种：

不论是连续模式，还是断续模式，都会有上升尖峰或者是下降尖峰，无非是大小的问题。

如果我们拉开来看，尖峰可以看出来是一个振荡波形，频率很高。

或者更明显的，断续模式中，在电感电流降低为0时就开始振荡，幅度不小，并且频率也不高。

对于新手来说，可能在心里打鼓：这个振荡莫不是有什么问题？

上面这些振荡，或是尖峰，要理解为什么长成这样？有没有问题？如何抑制？如果要详细了解来龙去脉，其实并不是很容易。

这些波形，本质上就是LC阻尼振荡，这一节我们先搞明白LC阻尼振荡的各种情况。

LC阻尼振荡

上面说的这些波形，产生的机理就是，在开关断开之前，电感或电容被充电。而在开关断开之后，电感或电容的能量需要释放，因此会找到电路中的寄生电容或是寄生电感，再结合电路中的等效电阻，组成了LC阻尼振荡。

Buck具体是如何构成LRC回路的，因为涉及到很多寄生参数，这个也不容易搞清楚，后面专门细说。

这节的主题就是LC阻尼振荡。

我们就以最简单的LRC串联电路来举例

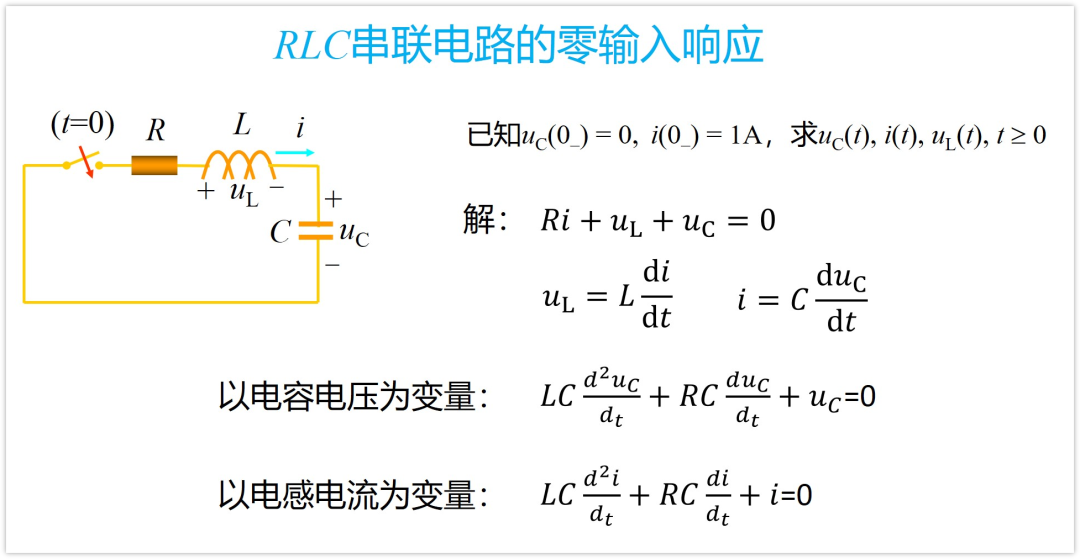
这个电路其实在大学课程《电路分析》应该有学过（好像《信号与系统》这门课也有），就是一个二阶电路。

这个电路的波形分为四种情况，分别是：

最近get一个新技能，试着使用了一下LTspice仿真，感觉还不错，比Matlab方便吧。当然，也只能说明两个软件侧重点不一样吧，Matlab是数学工具，如果能用Matlab搞出下面的结果，理解肯定会更加的深入，但是难度更高吧。

下面来看下我做的LTspice仿真：

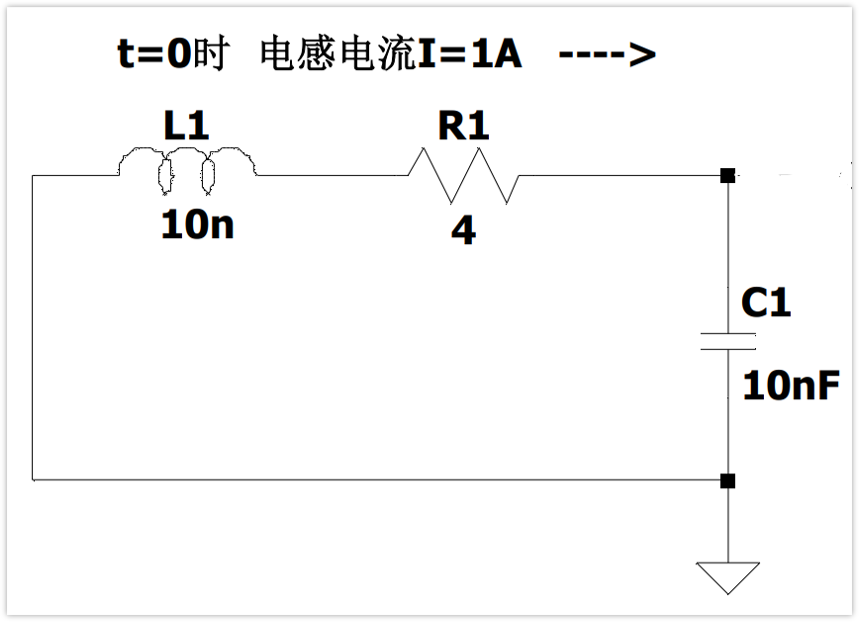
初始条件：L=10nH C=10nF 初始电感电流I=1A，电容电压为0V。

根据公式2(L/C)^0.5求得临界阻尼电阻R=2Ω。

下面我们只改变电阻R，让R=4Ω，2Ω，1Ω，0.1Ω，0Ω，分别来看看波形：

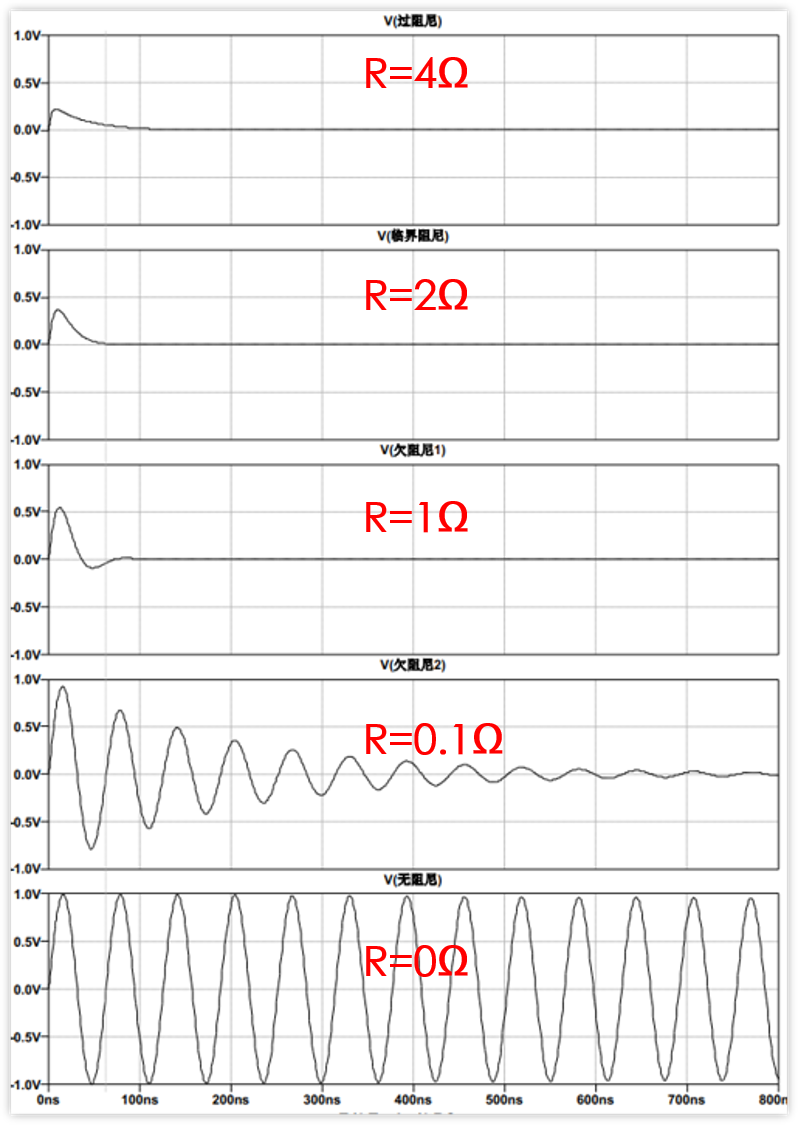
从上图我们可以得到振荡频率：

我们对比R=0.1和R=0的波形，可以看到，振荡的周期（两个波峰的时间差）是一样的，都是62.8ns左右，其实这就等于LC电路的谐振频率。

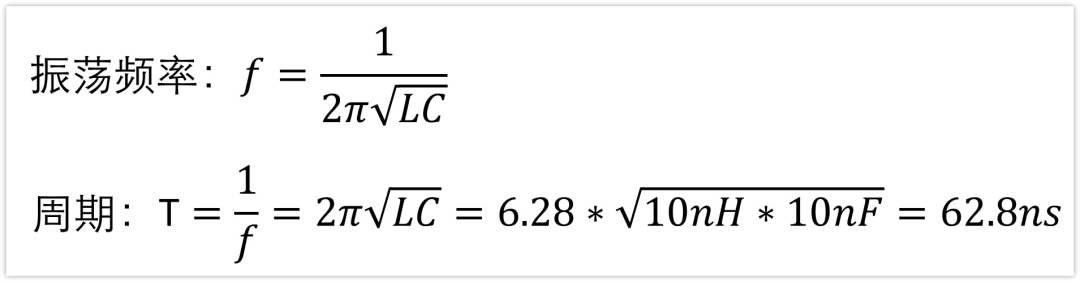
知道这个频率有什么用呢？

我们可以根据这个得到电路中总的电感或是电容多大。

实际应用中，我们通常可以用示波器量出振荡尖峰的频率，然后我们可以人为并上一个电容，这时尖峰频率肯定会发生变化，我们再用示波器测出来。

根据前后的频率，增加的电容容量，我们就可以算出寄生电容和电感是多大。

以下是某文档讲解的snuber电路（BUCK电路中常用于去尖峰）

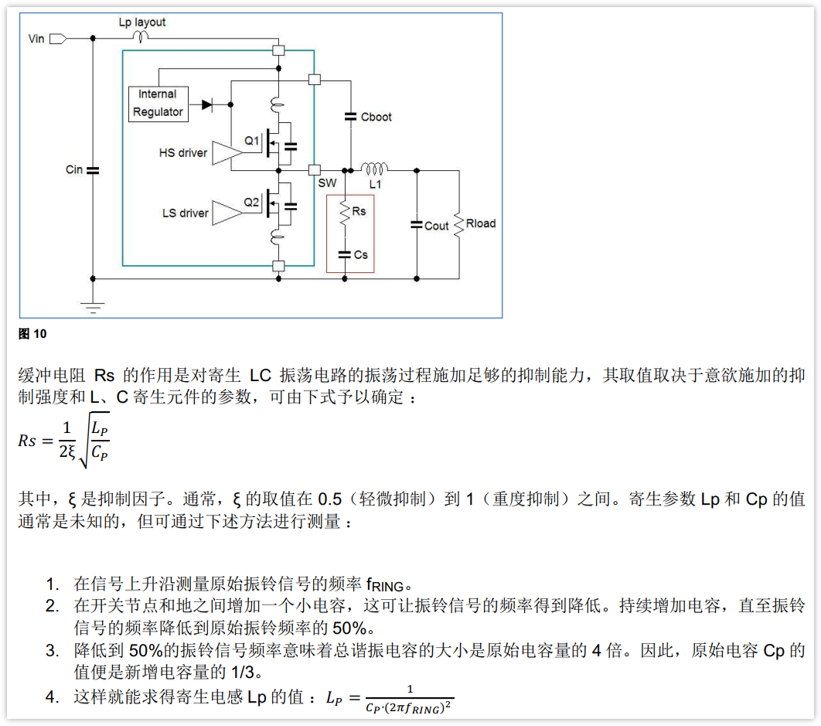
现在应该这种方法的基本原理了吧。

本节内容到这里就结束了，主要是理论的，后面会使用LTspice仿真，研究下开篇说的几个振荡波形，感谢大家阅读。

责任编辑：lq6