剖析经典滤波算法的图像复原技术研究

1 引言

图像增强是指按特定的需要突出一幅图像中的某些信息，同时削弱或者去除某些不需要的信息的处理方法。图像增强技术就是把图像中对观测者有用的信息加以增强，使图像使用起来更方便、视觉效果更好。

比如使淹没在噪声中的图像呈现出来，或者把对比度低的图像显示成对比度高的图像，或加强空间频率的高频分量，使图像色调清晰等。常规的图像增强方法有直方图均衡、同态增晰等。直方图均衡法是一种常用的技术，对于直方图范围不大的图像增强是非常有效的。

但是，对于某些灰度频数较小的区域，对比度将会被减弱，甚至会消除这部分信息。另外，直方图均衡法对噪声比较敏感，在增强图像视觉效果的同时也会增强噪声。

图像退化是指由于成像系统受到各种因素的影响，使得图像质量降低。引起图像退化的原因有成像系统的散焦；成像设备与物体的相对运动；成像器材的固有缺陷；外部干扰等。图像复原可以看作是图像退化的逆过程，是将图像退化的过程加以估计，建立退化的数学模型后，补偿退化过程造成的失真。

图像恢复存在的困难，主要是因为退化过程并不知晓，这种情况下的复原属于盲目复原。由于图像模糊的同时，噪声和干扰也会同时存在，这也为图像复原带来了困难和不确定性。

光学图像的噪声主要来源于图像的获取和传输过程。图像获取的数字化过程，如图像传感器的质量和环境条件。图像传输过程中传输信道的噪声干扰，如通过无线网络传输的图像会受到光或其它大气因素的干扰。

经典的去噪滤波算法主要是去除高频分量，比如噪声，当然也会去除边缘和角点等细节信息，通常人们的视觉主要集中于图像中间位置，对于边缘部分不太关注，因此，对比研究经典滤波算法在去除图像噪声恢复原始图像中仍然十分有用。

2 经典滤波算法去噪复原技术

2.1图像复原国内外研究现状

图像复原也叫图像恢复，是图像处理中的一大类技术。无论是由光学，还是电子方法获得的图像都会有不同程度的退化。由于获得图像的方法不同，其退化形式也是多种多样，如传感器噪声、摄像机聚焦不准确、物体与摄像设备之间的相对移动、随机大气湍流、光学系统的相差、成像光源或射线的散射等，这些因素都会使成像的分辨率和对比度退化。

图像复原和图像增强有密切的联系，相同之处是，它们都要得到在某种意义上改进的图像。不同之处是，图像增强技术一般要借助人的视觉系统的特性以取得看起来较好的视觉效果，而图像复原则认为图像在某种情况下退化或恶化了（图像品质下降），需要根据相应的退化模型和知识重建或恢复原始图像。

数字图像处理研究很大部分都是致力于图像复原，包括对算法的研究和对特定问题的图像处理程序的编制，国内外学者都有相关的研究。对于退化的复原，一般采用两种方法。一种方法是适用于对图像缺乏先验知识的情况。

此时可对退化过程（模糊和噪声）建立模型，进而寻找一种去除或者削弱其影响的过程。另一种方法，若对于原始图像有足够的先验知识，则对原始图像建立一个数学模型，并根据它对退化图像进行拟合会更有效。

下面给出通用的退化模型，如图2-1所示。在该模型中，图像退化过程被模型化为一个作用在输入图像f（x，y）上的系统h（x，y）。它与一个加性噪声n（x，y）的联合作用导致退化图像g（x，y）。根据这个模型恢复图像就是要在给定g（x，y）和代表退化的h（x，y）的基础上得到对f（x，y）的某个近似过程。假设已知n（x，y）的统计特性。

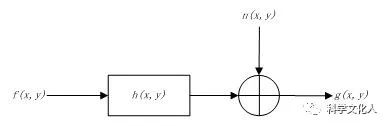
图2-1 通用图像退化模型

2.1.1 图像噪声滤波

图像被噪声污染是计算机视觉和图像处理经常要考虑的情形。图像噪声的类型很多，如加性噪声、乘性噪声、量化噪声、椒盐噪声等。一般的原始图像都混有各种噪声，主要表现为高斯噪声和椒盐噪声。椒盐噪声的形成通常不依赖于其相邻像素，而是随机产生，在图像中表现为黑色或白色的污点。其产生的原因通常是由于传输错误、相机传感器元件缺陷或者寄存器的错误定位等引起。

滤噪是图像预处理的一个基本内容，其目标实在滤除噪声的同时尽可能地保留图像的边缘和细节特征。现在的滤波方法有很多，大致可分为线性方法和非线性方法。图像中混入的高斯噪声，一般采用线性的均值滤波；

对于图像中混入的椒盐噪声，一般采用非线性方法的中值滤波。中值滤波算法主要针对椒盐噪声进行滤波，后来提出了一系列改进型中值滤波，包括加权中值滤波［1］，中心加权中值滤波［2］以及多级中值滤波［3］等。

高斯噪声与椒盐噪声有较大的不同，椒盐噪声为极端噪声，只污染一部分像素，受高斯噪声污染的图像每一个像素都会受到污染。对于同时受到椒盐噪声和高斯噪声污染的图像，通常采用的方法是先采用中值滤波方法消除图像中的椒盐噪声，再用均值滤波方法去除高斯噪声。

国内外学者相继提出了自适应加权均值滤波［4］、基于局部统计的滤波器［5］、权值排序统计滤波器［6］以及基于神经网络技术的滤波器［7］等。

对高污染椒盐噪声的滤波方法国内外学者也进行了部分研究，如对噪声监测和滤波都采用反复递归的PSM算法［8］、Wei-Yu and Ja-Chen-Lin［9］提出了一种MMEM（Minimum-Maximum Exclusive Mean）滤波器来处理高污染噪声图像。Minggang Ma［10］和Mituhiro Okano等［11］把模糊技术引入高污染图像滤波中，Shih-Mao Lu［12］等采用了神经网络的方法。

2.2 几种经典滤波算法

2.2.1 中值滤波

中值滤波是一种非线性信号处理方法，与其对应的中值滤波器也就是一种非线性滤波器。

中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值。中值滤波在一定的条件下可以克服线性滤波带来的图像细节模糊问题，且适用于滤除脉冲干扰及图像扫描噪声；

而且，其在使用中不需要分析图像的统计特性。中值滤波法对消除椒盐噪声非常有效，在光学测量条纹图象的相位分析处理方法中有特殊作用，但在条纹中心分析方法中作用不大。对一些细节多，特别是点、线、尖部多的图像，不宜采用中值滤波方法。

2.2.2 高斯平滑滤波

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

2.2.3 维纳滤波

维纳滤波（wiener filtering） 是一种基于最小均方误差准则、对平稳过程的最优估计器。这种滤波器的输出与期望输出之间的均方误差为最小，因此，它是一个最佳滤波系统。它可用于提取被平稳噪声所污染的信号。

从连续的（或离散的）输入数据中滤除噪声和干扰以提取有用信息的过程称为滤波，这是信号处理中经常采用的主要方法之一，具有十分重要的应用价值，而相应的装置称为滤波器。根据滤波器的输出是否为输入的线性函数，可将它分为线性滤波器和非线性滤波器两种。维纳滤波器是一种线性滤波器。

2.3 经典滤波算法原理

2.3.1 中值滤波原理

中值滤波是基于排序统计理论的一种能有效抑制噪声的非线性信号处理技术，中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替，让周围的像素值接近的真实值，从而消除孤立的噪声点。

方法是用某种结构的二维滑动模板，将板内像素按照像素值的大小进行排序，生成单调上升（或下降）的为二维数据序列。二维中值滤波输出为g（x， y）=med{f（x-k， y-l），（k， l∈ W）}，其中，f（x， y）、g（x， y）分别为原始图像和处理后图像。W为二维模板，通常为3*3，5*5区域，也可以是不同的的形状，如线状，圆形，十字形，圆环形等。

2.3.2 高斯平滑滤波原理

由于高斯函数的傅立叶变换仍是高斯函数， 因此高斯函数能构成一个在频域具有平滑性能的低通滤波器。可以通过在频域做乘积来实现高斯滤波。均值滤波是对信号进行局部平均， 以平均值来代表该像素点的灰度值。

矩形滤波器（Averaging Box Filter）对这个二维矢量的每一个分量进行独立的平滑处理。通过计算和转化 ，得到一幅单位矢量图。这个 512×512的矢量图被划分成一个 8×8的小区域 ，再在每一个小区域中 ，统计这个区域内的主要方向 ，亦即将对该区域内点方向数进行统计，最多的方向作为区域的主方向。

于是就得到了一个新的64×64的矢量图。这个新的矢量图还可以采用一个 3×3模板进行进一步的平滑。

高斯滤波实质上是一种信号的滤波器，其用途是信号的平滑处理，人们知道数字图像用于后期应用，其噪声是最大的问题，由于误差会累计传递等原因，很多图像处理教材会在很早的时候介绍Gauss滤波器，用于得到信噪比SNR较高的图像（反映真实信号）。

与此相关的有Gauss-Laplace变换，其实就是为了得到较好的图像边缘，先对图像做Gauss平滑滤波，剔除噪声，然后求二阶导矢，用二阶导的过零点确定边缘，在计算时也是频域乘积=》空域卷积。

滤波器就是建立的一个数学模型，通过这个模型来将图像数据进行能量转化，噪声就是属于高频率部分，高斯滤波器平滑处理后降低噪声的影响。

2.3.3 维纳滤波原理

维纳滤波的基本原理是：设观察信号y（t）含有彼此统计独立的期望信号x（t）和白噪声ω（t）可用维纳滤波从观察信号y（t）中恢复期望信号x（t）。设线性滤波器的冲击响应为h（t），此时其输入y（t）为y（t）=x（t）+w（t），输出：

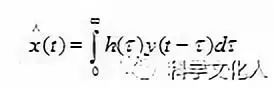
（2-1）

从而，可以得到输出。

对x（t）期望信号的误差为

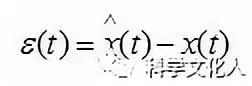
（2-2）

其均方误差为

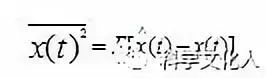
（2-3）

E［ ］表示数学期望。应用数学方法求最小均方误差时的线性滤波器的冲击响应hopt（t）可得如（4）方程。

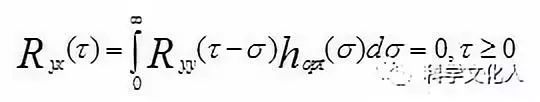
（2-4）

式中，Ryx（t）为y（t）与x（t）的互相关函数，Ryy（τ-σ）为y（t）的自相关函数。上述方程称为维纳-霍夫（Wiener-Hopf）方程。求解维纳-霍夫方程可以得到最佳滤波器的冲击响应hopt（t）。在一般情况下，求解上述方程是有一定困难的，因此这在一定程度上限制了这一滤波理论的应用。然而，维纳滤波对滤波和预测理论的开拓，影响着以后这一领域的发展。

2.4 设计过程

2.4.1 原始彩色图像灰度化

本课程设计题目要求为：给定一幅模糊或含噪的图像，用图像增强或图像复原技术，改善图像质量，并给出PSNR指标。

基于本题目，给出如下的设计过程。首先读取一幅原始清晰图像并将其灰度化，然后添加不同类型的噪声，对加噪图像进行滤波算法处理，最后计算恢复图像与原始灰度图像的峰值信噪比，因此整个设计过程如2-2所示。

图2-2 图像复原处理过程

在Matlab编程时，可以预先在程序文件夹目录里存放一张彩色（或灰度）图片，通过imread函数读取图片。当然也可以直接读取Matlab图片库中的图片。通过rgb2gray函数将彩色图像转化为灰度图像，以便于后续处理。图2-3为读取一幅彩色图像与其灰度化图像。

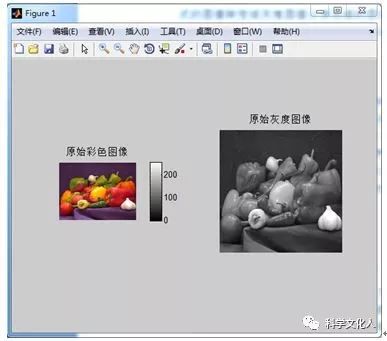
图2-3 原始彩色图像与其灰度图

将彩色图像转化成为灰度图像的过程称为图像的灰度化处理。彩色图像中的每个像素的颜色有R、G、B三个分量决定，而每个分量有255中值可取，这样一个像素点可以有1600多万（255*255*255）的颜色的变化范围。

而灰度图像是R、G、B三个分量相同的一种特殊的彩色图像，其一个像素点的变化范围为255种，所以在数字图像处理种一般先将各种格式的图像转变成灰度图像以使后续的图像的计算量变得少一些。灰度图像的描述与彩色图像一样仍然反映了整幅图像的整体和局部的色度和亮度等级的分布和特征。图像的灰度化处理可用两种方法来实现。

第一种方法使求出每个像素点的R、G、B三个分量的平均值，然后将这个平均值赋予给这个像素的三个分量。

第二种方法是根据YUV的颜色空间中，Y的分量的物理意义是点的亮度，由该值反映亮度等级，根据RGB和YUV颜色空间的变化关系可建立亮度Y与R、G、B三个颜色分量的对应：Y=0.3R+0.59G+0.11B，以这个亮度值表达图像的灰度值。

2.4.2 灰度图像加噪处理

为了模拟一幅受到污染的图像，以及后续的峰值信噪比计算，可以通过给原始图像加噪处理，模拟图像退化过程，并且可通过滤波器检验滤波算法的处理能力，比较不同滤波器对不同噪声的滤波效果。本次设计中，对原始灰度图像分别添加椒盐噪声、高斯噪声、乘性噪声，并绘制灰度图像和加噪后图像的直方图。图2-4给出了分别添加三中噪声后的图像，图2-5为对应的直方图。

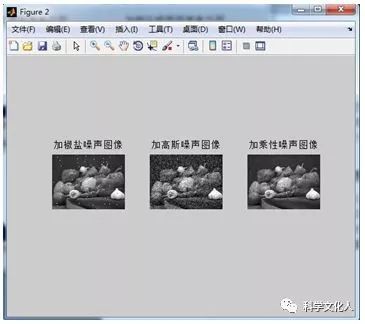
图2-4 加噪图像

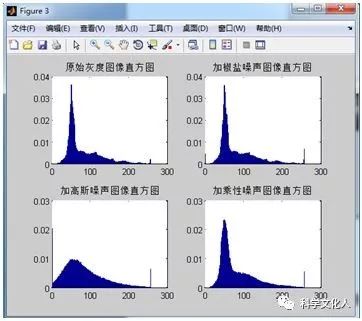
图2-5原始灰度图像与加噪图像直方图

2.4.3 加噪图像滤波处理

在上一小节中，通过添加噪声模拟了图像退化过程，本小节将针对收到不同噪声污染的图像，通过中值滤波、高斯平滑滤波和维纳滤波进行处理。

（1）对于椒盐噪声，分别通过中值滤波算法、高斯平滑滤波算法和维纳滤波算法进行去噪，可通过视觉观察去噪效果。图2-6给出了三种滤波器针对椒盐噪声的去噪结果。图2-7为原始灰度图像和三种滤波算法下的去噪图像的直方图。直观可以观察看出，针对椒盐噪声，中值滤波具有较好的效果。

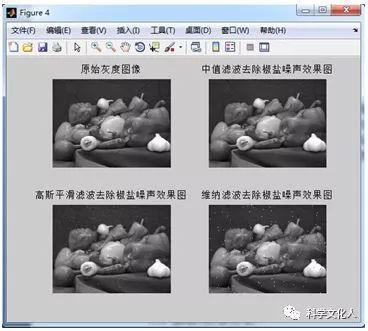
图2-6去除椒盐噪声效果对比图

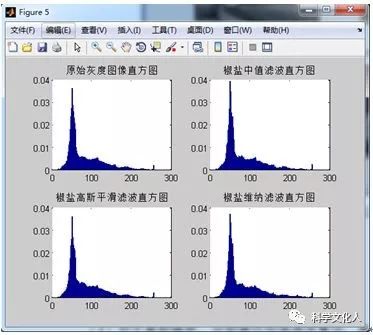
2-7去椒盐噪声直方图

（2）对于高斯噪声，分别通过中值滤波算法、高斯平滑滤波算法和维纳滤波算法进行去噪，可通过视觉观察去噪效果。图2-8给出了高斯噪声在三种滤波算法处理下的结果。图2-9为原始灰度图像和三种滤波算法下的去噪图像的直方图。从图2-8可以看出，维纳滤波去除高斯噪声较好，从图2-9的直方图比较中也可以看出。

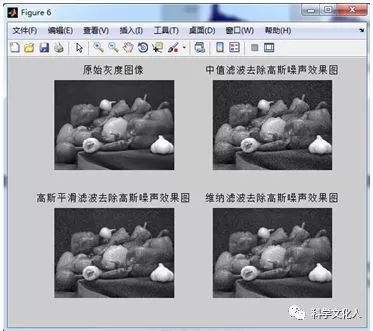
图2-8去除高斯噪声效果对比图

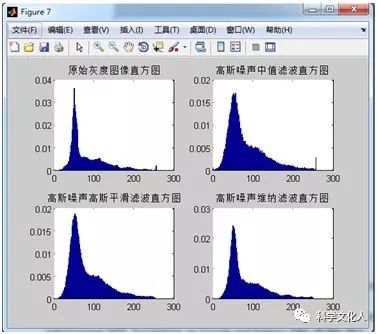
2-9去高斯噪声直方图

（3）对于乘性噪声，分别通过中值滤波算法、高斯平滑滤波算法和维纳滤波算法进行去噪，可通过视觉观察去噪效果。图2-10给出了乘性噪声在三种滤波算法处理下的结果。图2-11为原始灰度图像和三种滤波算法下的去噪图像的直方图。从图2-10和图2-11中可以看出，对于乘性噪声，高斯平滑滤波和维纳滤波算法均具有比较好的效果，而中值滤波要差一些。

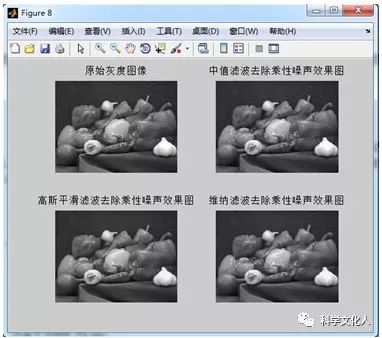
图2-10去除乘性噪声效果对比图

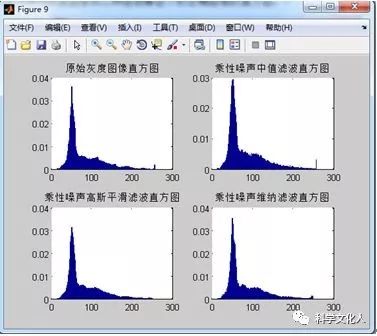
2-11去乘性噪声直方图

从2.4.3节内容可以得知对于不同的噪声，不同的滤波算法有不同的处理效果，并且可以通过滤波效果图和直方图直观看出。为了更具体和更具说服力，我们通过可以通过计算图像的峰值信噪比（PSNR）对图像的恢复质量进行客观而有效的评价。

峰值信噪比（Peak Signal to Noise Ratio，PSNR）是衡量图像失真或噪声水平的客观标准。两个图像之间PSNR值越大，则越相似。PSNR定义式：

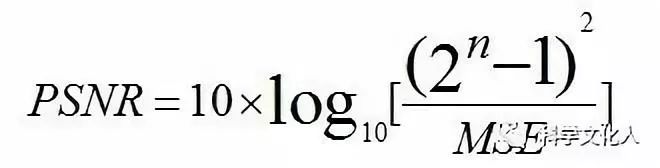
（2-5）

其中，n是每个采样值的比特数，MSE是原图像与处理图像之间的均方误差，PSNR的单位为dB。

3 结果分析

3.1滤波效果分析

通过前文2.4.3小节研究内容可知，对于椒盐噪声，采用中值滤波算法处理效果比较好；对于高斯噪声，采用维纳滤波算法处理效果比较好；对于乘性噪声，采用高斯平滑滤波算法或维纳滤波算法处理比较好。为了更客观的比较，3.2节PSNR对比中精确描述。

3.2 PSNR对比

为了更加客观描述图像复原质量的评价，针对椒盐噪声、高斯噪声、乘性噪声，各自采用中值滤波算法、高斯平滑滤波算法以及维纳滤波算法，得到相对的图像复原结果，并通过Matlab程序计算PSNR，通过下面各表列出。

4 结论

通过前文的研究，对于一幅受到噪声污染的图像，通过常用的经典滤波算法进行复原，会产生不同的效果。对于椒盐噪声，采用中值滤波算法处理效果比较好；对于高斯噪声，采用维纳滤波算法处理效果比较好；对于乘性噪声，采用高斯平滑滤波算法或维纳滤波算法处理比较好。

需要注意的是，由于选择读取图像的原因，经过复原后的图像计算出的PSNR值几乎均未超过30dB，若更改为其他合适图像，可以得到较高的PSNR值。

另外，经过测试发现，如果添加的噪声浓度过大，则会导致滤波算法效果下降，降噪性能受到限制，需要对算法进行改进，或者选用其他有效算法进行图像复原和增强。

考虑到研究深度，本设计只涉及基础滤波算法在图像复原中的应用，未对更多改进型有效算法展开深入研究。通过本次设计，为基本噪声图像复原技术提供了参考。

编辑：jq