C语言排序中堆排序的技巧

堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

对于堆的操作通常需要以下3个步骤：

最大堆调整（Max Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点

创建最大堆（Build Max Heap）：将堆中的所有数据重新排序

堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算。

C代码实现

代码看起来比较抽象，将代码运行时数据交换的过程打印出来，然后结合二叉树的图形来分析，就会比较好理解了。代码运行过程中数据交换过程如下：

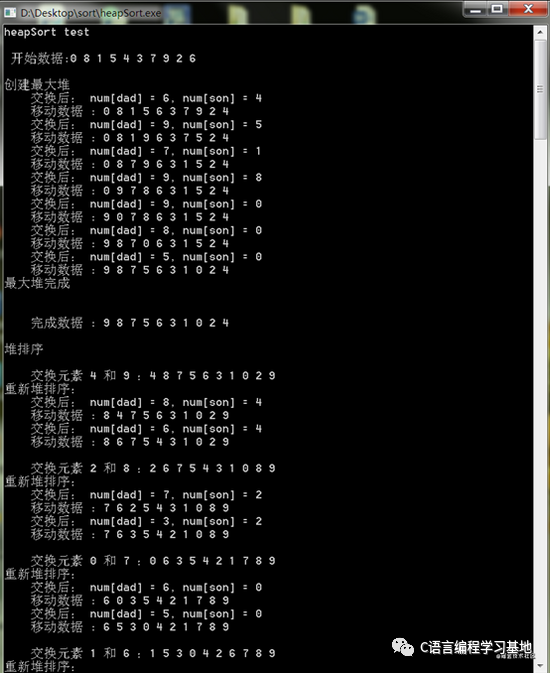
为了方便观看这里使用二叉树图形生成软件，通过二叉树图形来观察数据交换过程。二叉树图形生成使用的是一个在线生成网站：mshang.ca/syntree 后面所有的二叉树图形都使用此软件生成。

代码一开始首先打印出原始数据

数组元素 0 8 1 5 4 3 7 9 2 6 将这10个数据在网站上使用公式生成二叉树的图表，软件界面如下：

首先将数组从上至下按顺序排列，转换成二叉树。

公式：0［8 ［5 9［2］］［4［6］］］ ［1［3］ ［7 ］］］

转换成二叉树之后，需要让这个无序堆变成最大堆，也就是每个堆都实现父节点的值大于任何一个子节点值。从最后一个堆开始，依次比较父节点和子节点的值，如果子节点值大于父节点值，就需要交换。

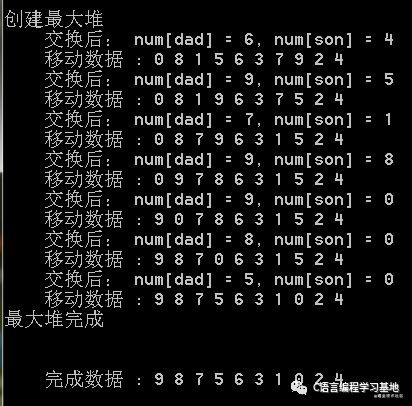
创建最大堆： 6为最后一个子节点，所以从6开始依次和父节点比较，如果子节点大于父节点，就需要交换子节点和父节点的位置。从设备树图形中可以看出，子节点6大于父节点4，所以需要交换子节点的父节点的位置。

公式：0［8 ［5 9［2］］［6［4］］］ ［1［3］ ［7 ］］］

交换 6 和4

6交换完成后，接下来依次向前比较其他子节点，6前面的节点是2，2小于父节点5，继续向前查找子节点9，子节点9大于父节点5，所以就交换9和5的位置。

公式：0［8 ［9 5［2］］［6［4］］］ ［1［3］ ［7 ］］］

交换9和5

接下来继续向前查找，发现子节点7大于父节点1，继续交换。

公式：0［8 ［9 5［2］］［6［4］］］ ［7［3］ ［1 ］］］

交换7和1

继续向前查找发现子节点9大于父节点8，交换位置。

公式：0［9 ［8 5［2］］［6［4］］］ ［7［3］ ［1 ］］］

交换9和8

继续比较其他节点

公式：9［0 ［8 5［2］］［6［4］］］ ［7［3］ ［1 ］］］

交换9和0

公式：9［8 ［0 5［2］］［6［4］］］ ［7［3］ ［1 ］］］

交换8和0

公式：9［8 ［5 0［2］］［6［4］］］ ［7［3］ ［1 ］］］

交换5和0

此时最大堆已经创建完成，此时根节点的数字9就是数组中的最大值。

代码中打印出来的数据顺序和通过二叉树图形分析出来的顺序完全一样。此时最大堆调整已经完成了。接下来就需要开始堆排序，依次将根节点的数据存放到最后一个节点，形成一个有序堆。

堆排序（最大堆调整）

首先交换数组中第一个元素，和排序好的前一个元素位置。此时数组中的第一个元素是9，排序完成之后最后一个元素是4，交换9和4.

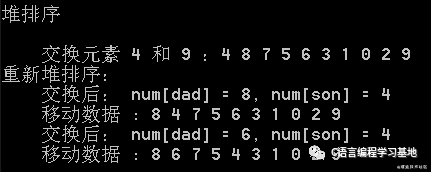
公式：4［8 ［5 0［2］］［6［9］］］ ［7［3］ ［1 ］］］

交换9和4

交换完成后，此时最大值9所在的底部位置就成为了有序区，有序区之后就不会参与任何对比。接下来继续调整父节点和子节点，确保父节点要大于子节点。

公式：8［4 ［5 0［2］］［6［9］］］ ［7［3］ ［1 ］］］

交换8和4

公式：8［6 ［5 0［2］］［4［9］］］ ［7［3］ ［1 ］］］

交换6和4

此时数字8称为了根节点，是目前无序区中的最大值，将8和底部区的2交换，将当前最大值8放到有序区中。

公式：2［6 ［5 0［8］］［4［9］］］ ［7［3］ ［1 ］］］

交换8和2

此时8已经存放到了有序区中，此后就不参与任何交换了。此时2变为根节点后，需要在重新调整一次节点，确保父节点大于子节点。

公式：7［6 ［5 0［8］］［4［9］］］ ［2［3］ ［1 ］］］

交换7和2

公式：7［6 ［5 0［8］］［4［9］］］ ［3［2］ ［1 ］］］

交换3和2

此时数字7变为根节点，是无序区间的最大值。需要将根节点的数字移动到有序区中。

将根节点7和0交换位置。

公式：0［6 ［5 7［8］］［4［9］］］ ［3［2］ ［1 ］］］

交换7和0

接下来重新调整节点 公式：6［0 ［5 7［8］］［4［9］］］ ［3［2］ ［1 ］］］

交换6和0

公式：6［5 ［0 7［8］］［4［9］］］ ［3［2］ ［1 ］］］

交换5和0

此时6变为了根节点，是无序区间的最大值。

将根节点和有序区间的前一个数字交换，也就是1和6需要交换。

公式：1［5 ［0 7［8］］［4［9］］］ ［3［2］ ［6 ］］］

交换6和1

接下来重新调节一次节点

公式：5［1 ［0 7［8］］［4［9］］］ ［3［2］ ［6 ］］］

交换5和1

公式：5［4 ［0 7［8］］［1［9］］］ ［3［2］ ［6 ］］］

交换4和1

此时5变成的根节点，需要将5移动到有序队列中去。

接下来需要交换根节点5和无序节点2的位置

公式：2［4 ［0 7［8］］［1［9］］］ ［3［5］ ［6 ］］］

交换5和2

重新调整节点位置

公式：4［2 ［0 7［8］］［1［9］］］ ［3［5］ ［6 ］］］

交换4和2

此时4是无序列表中的最大值，需要交换4和1的位置

公式：1［2 ［0 7［8］］［4［9］］］ ［3［5］ ［6 ］］］

交换4和1

重新调整节点位置

公式：9［2 ［0 6［7］］［3［8］］］ ［1［4］ ［5 ］］］

交换3和1

此时3为无序列表中最大值，需要交换3和0的位置。

公式：0［2 ［3 7［8］］［4［9］］］ ［1［5］ ［6 ］］］

交换3和0

交换完成后重新调整节点位置 公式：9［0 ［2 6［7］］［3［8］］］ ［1［4］ ［5 ］］］

交换2和0

此时2变成了无序列表中最大值，1为有序列表的前一个值，交换2和1的位置。

公式：1［0 ［3 7［8］］［4［9］］］ ［2［5］ ［6 ］］］

交换2和1

此时1是根节点，无序列表中就剩0一个数字了，交换1和0。

公式：0［1 ［3 7［8］］［4［9］］］ ［2［5］ ［6 ］］］

交换1和0

这是0变成了根节点，而其他的所有数字都在有序列表中，无序列表中已经没有数字了，此时说明排序完成。

可以看出最好、最坏、一般情况下数据移动的次数和方法基本都差不多。

接下来随机生成10000个数据，看看排序需要多长时间。

编辑：jq