简述MATLAB中传统信号如何处理

振动分析在工程领域很常见，汽车中的 NVH，风机的模态分析，塔架、叶片等机械件的振动频率分析，发电机轴承振动，飞机发动机阶次分析等等。经常提到的知识点像信号处理，FFT，阶次分析，频谱估计，包络谱分析，模态分析，频率响应函数估计等等。

傅里叶变换

要谈信号处理就离不开傅里叶变换。我们先从最常用的傅里叶变换开始。傅里叶变换的本质是从空间（希尔伯特空间）中找一组正交基向量 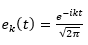或者正交基函数，正交意思是内积为 0，其中希尔伯特空间内积定义为：对于向量 f， g， 有

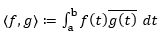
容易证明

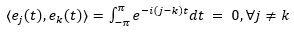
将时域信号投影到这组正交基上。傅里叶变换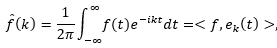也就可以看作 f（t） 在 k 对应的基 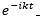上的投影。对于离散傅里叶变换（DFT）

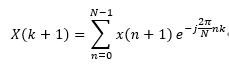
为了方便理解，我们先通过一个例子，利用 fft 函数（快速傅里叶变换，实现DFT的一种快速算法）将一段矩形信号（图中深蓝色信号）进行变换。通常我们得到幅值频率图像，可以看到对应频率的幅值。

为了更好的理解，我们把离散频率对应的正交基向量（图浅绿色）也绘制出来，对应图中浅绿色。方块绿则为幅值频率值，此处我们首先只选了前 20 个频率对应的基向量进行信号重构，得到图中红色信号。接下来，我们增加用于信号重建的基的数量，分别我们取前 60，前 300，发现信号越来越接近原始信号。

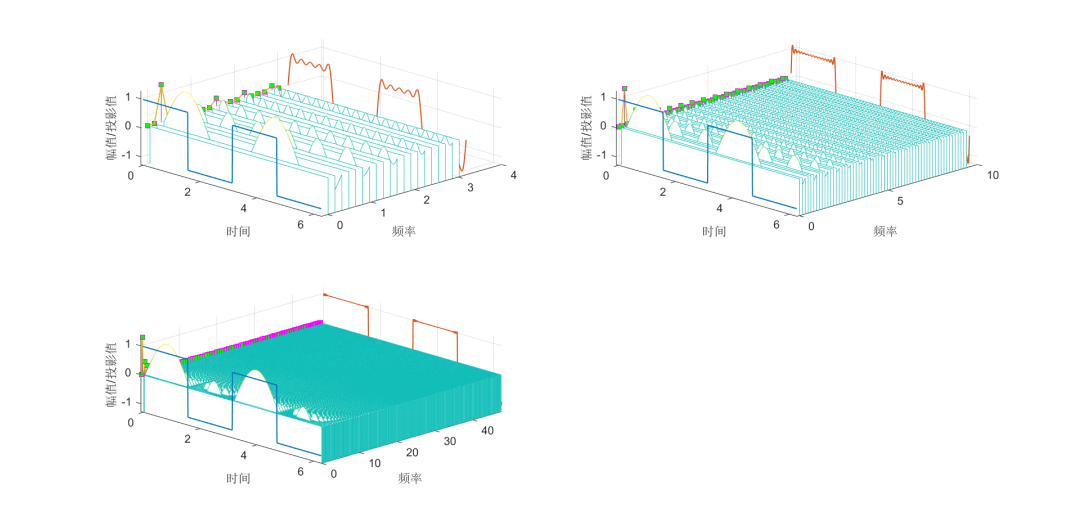
图表2

值得一提的是很多类似的程序会通过for循环来遍历各个基向量来实现上面的程序，但 MATLAB 中的矩阵思想更应该充分利用，既可以简化代码，又可以提升效率，例如程序中 baseSeries=cos（2*pi*Dfreq‘*t+Phi（1:length（Dfreq））’）计算得到的 baseSeries 变量是一个 n*m 矩阵，包含了所有的基向量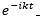n 是基向量的个数（k 的个数），m 是时域信号长度（t 的长度）。简单理解了傅里叶变换，接下来我们就可以使用 fft 进行一个初步的转动数据分析，我们先生成一段时长 2s，采样频率 600Hz 的数据，在这 2s 中，系统一直以 20Hz 的转速运行。

通过 fft 我们可以得到信号在对应转速的 20Hz 频率上幅值最大。这部分有很多重要的概念，包括时域/频域分辨率，频谱泄露，功率谱/能量谱等等。频率分辨率简言之就是区分两个不同频率的能力。假设信号的采样频率为 Fs， 在时域上，tn= n*Fs 反映的是时间轴，T=N*Fs 反映的是信号总时长，在频域上，我们可以得到 N 个频率（基向量），可以理解为 Fs 被 N 个值平分，因此频率的分辨率为

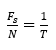
我们从上面推导可以知道频率分辨率由采样时长决定，如果采样时长太短，DFT 没有能力区分两个接近的频率值。

这里也给大家一个小练习，例如可以合成一段信号，由 90Hz 和 100Hz 两个频率组成，我们只选取 0.05s 长的数据：对应 DFT 的频率分辨率为 20Hz 》 （100Hz – 90Hz），然后进行 fft 变换，查看是否在频域上能够区分开这两个信号成分。

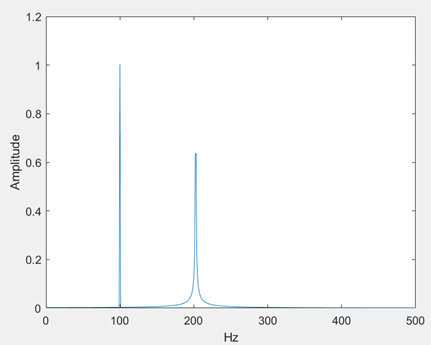
接下来我们通过一个由两个频率组成的正弦信号来介绍频谱泄露。详见 https://www.mathworks.com/help/releases/R2020b/signal/ug/amplitude-estimation-and-zero-padding.html这两种正弦波的频率分别为 f1 = 100Hz 和 f2 = 202.5 Hz。采样率为 1000Hz，信号长度为 1000 个采样点（T=1s）。我们期望的结果是频谱幅值只在 f1 = 100Hz 和 f2 = 202.5Hz 处的结果不为零，其他位置的频谱幅值为零。但真实结果是这样的：

图表4

也就是在 202.5Hz 的信号幅值被周围的频率值平分了，这种现象就是频谱泄露。从频谱分辨率的角度解释通过上面的结论：我们得到DFT的频率分辨率为 1/T = 1Hz，对于 f1 = 100Hz 正好落在分辨率的分仓边界上，而 f2 = 202.5Hz 不能被分辨率 1Hz 取整。

从时域角度解释：我们取了窗口时间 1s 长度的数据，对应 f1 的 100 个完整周期以及 f2 的 202.5 个周期，DFT 默认信号是采样时间窗内周期出现的无限长信号，因此当窗重复时对于f1来说正好是整数拼接，与原信号完全一致，而 f2 在上一个 1s 采样时间窗结束时并非对应信号自身周期结束，如下图：

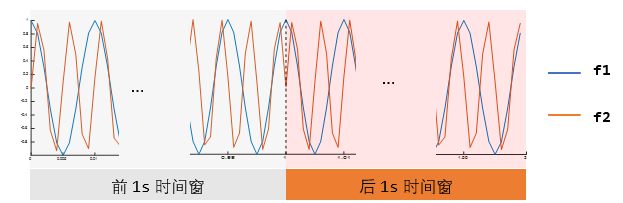
所以在上一个周期和下一个周期之间的信号过渡时有一个突变（周期边界由黑色虚线表示）。这个突变导致信号中添加了除原始频率之外的其他频率。这就解释了频谱泄露现象。频谱泄露会让我们在计算频域幅值时不够准确，因为能量幅值被周围的频率平分。

了解了频谱泄露的原因，我们可以通过调整采样时长，保证在每个时间窗口中都有原始信号的整数个周期，例如设置采样窗口 T = 2s（保证所有信号都是整数周期截断）。然而通常我们可能未必能对真实数据进行延长采样，可以考虑补零 zero-padding 的方式。

你可以用补零来对 DFT 进行插值。补零可以获得更准确的幅值估计。补零并不能提高 DFT 的谱（频率）分辨率。根据这种方法，将 DFT 要处理的信号用 0 补长到 2000 个点。有了这个长度，DFT 分仓之间的间距是 F_s=0.5Hz，在这种情况下，202.5Hz 正弦波的能量直接落在 DFT 分仓中。获得 DFT 并绘制振幅估计值得到更准确的幅值。

时频分析

在实际的应用中，信号经常是非平稳的，他们的频域是随时间在变化的，因此如果只用 FFT 无法反映出在什么时间里频域上的这种变化。为了回答在什么时刻出现什么频率的信号，我们需要进行时频分析。例如，给定一段信号，有两个 chirp 信号组成，第一个 chirp 信号在 0.1s 到 0.68s 一直存在，频率随时间 t 的函数是

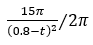
第二个 chirp 信号在 0.1s 到 0.75s 一直存在，频率随时间t的函数是

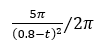
我们希望看到在不同时间轴上都各自有哪些频率出现。通过傅里叶变换（图表6），我们确实可以得到信号中包含的频域成分，但它回答不了各频率成分在什么时候出现。所以首先想到的是对原始数据加窗，每个窗口内做傅里叶变换。这就是短时傅里叶变换 STFT。STFT 提供了信号频率以及对应出现的时间信息。但是选择窗口大小是个问题。在短时傅里叶变换时频分析中，根据上面傅里叶变换的结论，选择较短的窗口大小可以得到较好的时间分辨率，但频率分辨率差。相反，选择较大的窗口会获得较好的频率分辨率，但时间分辨率差。而且一旦选择了窗口大小，它将在整个分析中保持不变。

如果可以提前知道待估计信号中我们想要的的频率分量，则可以根据这些需求来选择一个合适的窗口大小。两个 chirp 信号的在初始时间点的瞬时频率约为5Hz和15Hz。我们先选定窗口大小为 200ms（对应的频率分辨率为 1/0.2s = 5Hz）。瞬时频率在信号的前段被分辨出来，但在后段就不那么好了（后段频率变化快，时间分辨率不够会导致频带太宽）。

我们把窗口缩短为 50ms（对应的频率分辨率 1/0.05s = 20Hz），虽然在后面高频率差中可以分辨（时间分辨率更好），但在初始时刻低频率差中分辨不开（频率分辨率差）。

对于这种非平稳双曲线 chirp 信号，STFT 很难找到合适的时间窗口大小使得对整个频域的各频率都能分辨的很好。连续小波变换（CWT）可以解决 STFT 固有的分辨率问题。连续小波变换得时间窗口是可变的。如下图：

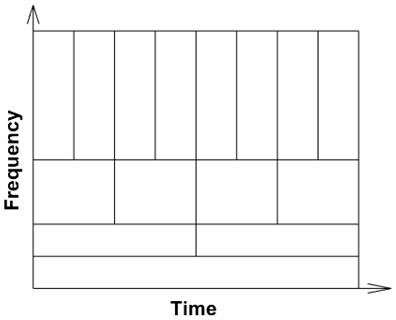
图表10如果要分析的信号主要是缓慢震荡的低频信号，而高频信号只是在一些瞬态时长或突变过程出现，这种情况可以考虑连续小波变换。如果高频信号持续时间很长并且是信号中的主要成分，这种情况使用连续小波变换就不合适了。

绘制 CWT 的时频图。时频图颜色对应幅值，频率轴用对数值，因为 CWT 中的频率是对数的。从图中可以清楚地看出信号中存在两个双曲 chirp 信号。使用连续小波变换，可以准确地估计整个信号周期在某个瞬时出现的频率成分，而不必手动设置窗口长度。

有人可能会问白色虚线是什么？白色虚线是 COI（cone of influence （COI）），我们可以确定白色虚线以内的数据是准确的。在阴影区域的白线之外，时频图中的信息应被视为不准确的信息，因为可能存在边缘效应。可以从时间分辨率的角度去看在低频对应较大尺度小波从而时间分辨率较差。

详细解释请查看：Boundary Effects and the Cone of Influencehttps://www.mathworks.com/help/releases/R2020b/wavelet/ug/boundary-effects-and-the-cone-of-influence.html通过 3D 可视化查看小波幅值的增长速率，同时也可以将 CWT 的结果和真实瞬时频率结果进行对比可以发现：CWT 结果和真实瞬时频率一致性较好。

MATLAB 中提供了除了上述时频变换，还有例如 Constant-Q Gabor Transform，Empirical Mode Decomposition and Hilbert-Huang Transform 等等。欢迎大家查看文档搜索 https://ww2.mathworks.cn/help/。

振动分析

我们再回到振动场景本身，在进行时频分析时，我们经常使用阶次分析来确定发生在旋转机械中的频谱成分，从时域波形中追踪和提取阶次，计算不同阶次的平均谱值，通过估计频响函数、固有频率、阻尼比和模态振型进行试验模态分析，用时间同步平均法相干去除噪声，用包络谱分析磨损，为疲劳分析生成高周期雨流计数等等。

我们通过一个示例，对直升机在加速和减速过程机舱内的加速度传感器数据进行阶次分析从而确定振动源并进行优化来演示分析过程。当设备的转速随时间一直变化时，阶次分析可以用来计算噪声或振动。每个阶数对应某个参考转速的倍频。例如，一个信号的频率如果等于发动机转频的 2 倍，那阶数就是 2。

我们通过仿真得到直升机在加速和减速过程机舱内的加速度传感器数据。直升机有很多旋转部件，包括发动机，齿轮箱，主旋翼和尾翼。每个部件都以一个和主发动机固定的速比运转，每个部件都可能导致有害振动。示例中的信号是一个时域电压信号 vib， 按 fs = 500Hz 的频率进行采样。

数据还包含涡轮发动机的转速（rpm） vs 时间关系。通过数据可视化可以看到发动机转速在爬升和滑行过程变化，同时振动加速度幅值也跟转速有关。使用 RPM-Frequency 图可视化数据为了能对振动信号进行时频域的分析，我们可以使用 rpmfreqmap。这个函数计算信号的短时傅里叶变换生成 RPM-Frequency 图谱。

rpmfreqmap 函数生成一幅时频图像同时还有对应的转速时间图像，还有下面的几个数值参数。图中幅值默认使用均方根（RMS）。当然也可以通过选项设置来使用其他幅值指标，例如峰值或功率值。瀑布图按钮可以生成三维的瀑布图。

可以看到瀑布途中很多频率对应的幅值会随发动机转速变化而变化。这说明这些频率是发动机转频的阶次频率。在 RPM 峰值也对应着振动高幅值的成分，这些成分主要集中在 20-30Hz 之间。可以看到在当前默认的频率分辨率（fs/128=3.906Hz，rpmfreqmap 函数默认将采样率做 128 等分作为分辨率）不足以分辨一些转速峰值处的低频成分，因此，我们尝试将频率分辨率调小一些，设置为 1Hz。从结果可以看出1Hz分辨率的 RPM-frequency 图可以清晰分辨出这些成分。

从现在的结果来看，在 RPM 峰值处对应的低频成分可以被分辨出来，但同时我们也发现在转速快速变化时出现了严重的频率拖尾现象。这是因为在每个时间窗内随着发动机转速增加或变小，振动频率阶数也在变化，覆盖一个比较大的范围，从而导致一个较大的频谱带宽。

分辨率越高，要求时间窗采样时长也越长，其中包含的频率覆盖范围越广，模糊现象越明显。在直升机起飞或减速滑行阶段，通过提升分辨率会导致频率拖尾现象更严重。在这时，我么可以考虑使用阶次图来避免这种分辨率和包含频率带宽大小的矛盾。

使用 RPM 阶次图可视化数据函数 rpmordermap 生成阶次频谱图与 RPM 图，用于阶次分析。由于每个阶次是参考旋转速度的固定倍数，因此阶次图包含一条条直的阶次路径，都是 RPM 的函数。函数 rpmordermap 与 rpmfreqmap 使用相同的参数，对应的频域轴现在是阶次，而不是频率。使用 rpmfreqmap 可视化直升机数据的阶次图。指定阶次分辨率为 0.005 倍基频。

阶次图包含每个阶次的直线路径，每一阶对应着发动机转速的倍数对应的振动。阶次图可以清楚的看到每个频率成分与发动机转速的关系。与 RPM-频率图相比，频率拖尾现象显著被抑制。使用平均阶次频谱确定峰值阶次接下来，确定阶次图的峰值位置。寻找主旋翼和尾翼阶次的整数倍的阶次，对应着这些旋翼产生的振动。函数 rpmordermap 返回包含各阶次的阶次图和与时间对应的 RPM 值。通过分析数据以确定直升机舱内高振幅振动的对应阶次。计算并返回阶次图谱数据。

接下来，使用 orderspectrum 计算并绘制 map 的平均谱。该函数接受 rpmordermap 生成的阶次图表作为输入，并对时域取平均。

返回平均频谱值，并调用 findpeaks 以返回两个最高峰值的位置。

在图中大约 0.05 阶处可以看到两个间隔很近的主峰。阶次小于 1，因为振动频率低于发动机转速。分析峰值阶次随时间的变化接下来，使用 ordertrack 求峰值阶次的幅值随时间的变化。使用 map 作为输入，通过不带输出参数调用 ordertrack 来绘制两个峰值阶次的振幅。

随着发动机转速的增加，两个阶次的振幅都会增加。接下来，使用 orderwaveform 提取每个阶次对应的时域波形。提取出来的时域波形可以直接与原始振动信号进行比较。orderwaveform 使用 Vold-Kalman 滤波器提取特定阶次的时域波形。将两个峰值阶次对应的时域波形之和与原始信号进行比较。

减少机舱振动为了确定机舱振动的来源，我们可以将振动峰值对应的阶次和直升机旋转部件的阶次配合起来看。

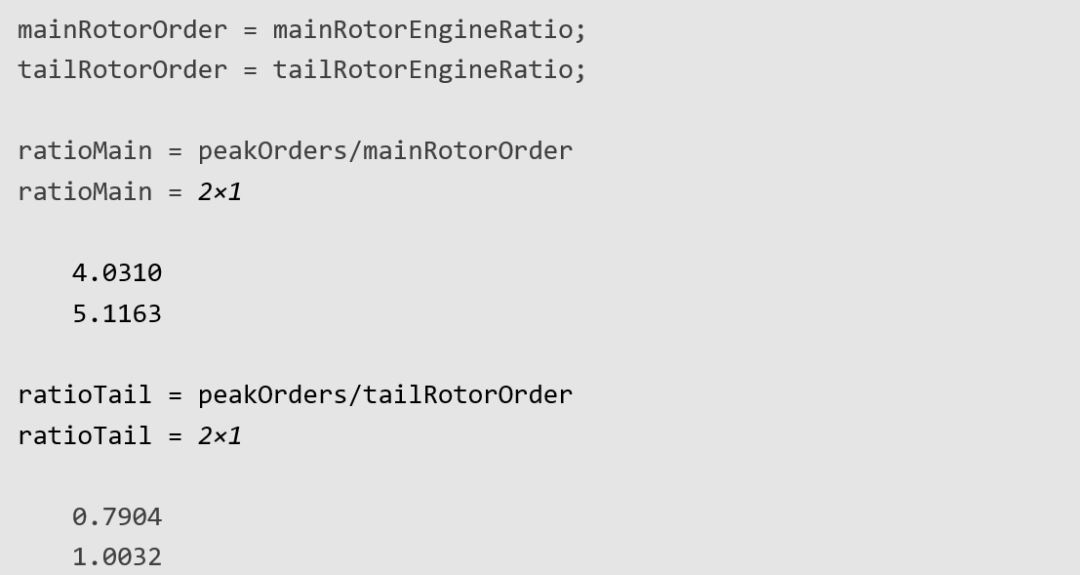
可以看到最大振幅分量的频率是主旋翼频率的四倍。而主旋翼有四个叶片，很可能是这种振动的来源，通常对于每个旋翼有 N 叶片的直升机来说，主转速的 N 阶振动是很常见的。同样，第二大分量位于尾旋翼速度的一阶次处，表明振动可能源于尾旋翼。在对主旋翼和尾旋翼进行轨迹和平衡调整后，采集新数据集。加载新数据集并比较调整前后的阶次频谱。

主峰的振幅现在大幅降低。

总结

此示例使用阶次分析来确定直升机的主旋翼和尾翼是否为机舱内高振幅振动的潜在来源。首先，使用了 rpmfreqmap 和 rpmordermap 对阶次进行可视化。RPM-阶次图在整个 RPM 范围内实现了阶次分离，且消除了在 RPM-频率图中出现的频率拖尾。

rpmordermap 最适合可视化在发动机加速和减速期间低 RPM 时的振动分量。接下来，该示例使用 orderspectrum 确定峰值阶次，使用 ordertrack 可视化峰值阶次的振幅随时间的变化情况，使用 orderwaveform 提取峰值阶次的时域波形。

最大的振幅振动分量出现在主旋翼旋转频率的四倍处，表明主旋翼叶片不平衡。第二大分量出现在尾旋翼的旋转频率处。调整旋翼后，振动程度得以降低。以后，我们还将陆续为大家介绍此系列的其他两个主题：模态分析与预测性维护：人工智能算法应用。

编辑：jq