以为只用了递归,其实还用了回溯
257. 二叉树的所有路径
题目地址:https://leetcode-cn.com/problems/binary-tree-paths/
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。
思路
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一一个路径在进入另一个路径。
前序遍历以及回溯的过程如图:
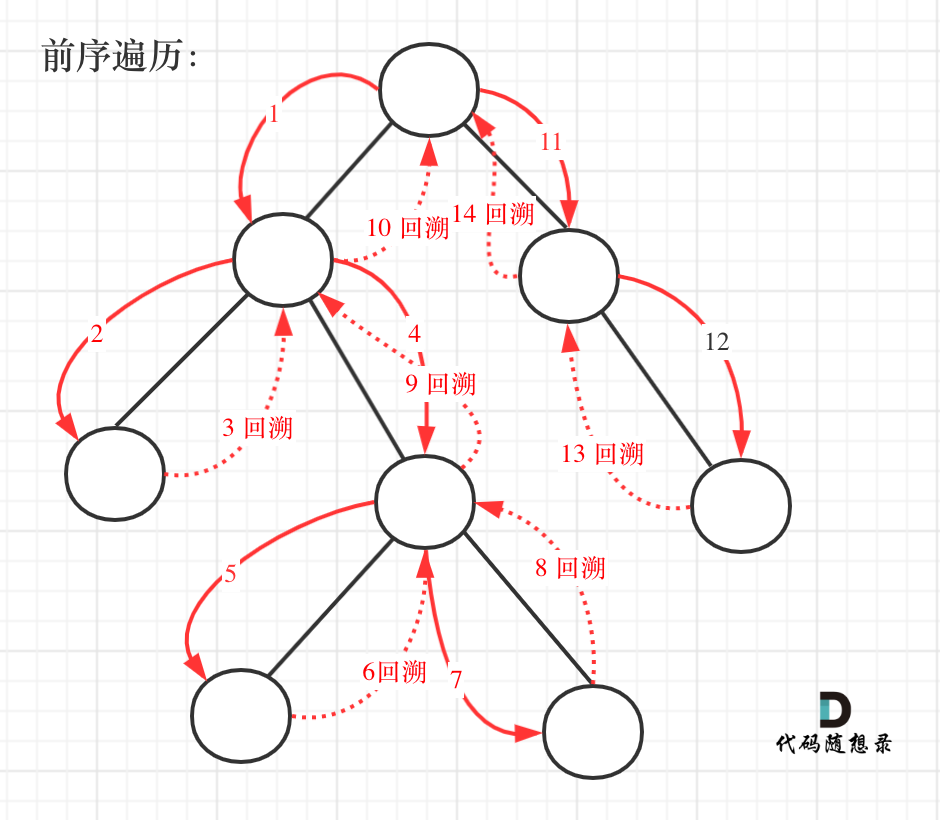
我们先使用递归的方式,来做前序遍历。要知道递归和回溯就是一家的,本题也需要回溯。
递归
递归函数函数参数以及返回值
要传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值,代码如下:
void traversal(TreeNode* cur, vector《int》& path, vector《string》& result)
确定递归终止条件
再写递归的时候都习惯了这么写:
if (cur == NULL) {
终止处理逻辑
}
但是本题的终止条件这样写会很麻烦,因为本题要找到叶子节点,就开始结束的处理逻辑了(把路径放进result里)。
那么什么时候算是找到了叶子节点? 是当 cur不为空,其左右孩子都为空的时候,就找到叶子节点。
所以本题的终止条件是:
if (cur-》left == NULL && cur-》right == NULL) {
终止处理逻辑
}
为什么没有判断cur是否为空呢,因为下面的逻辑可以控制空节点不入循环。
再来看一下终止处理的逻辑。
这里使用vector结构path来记录路径,所以要把vector结构的path转为string格式,在把这个string 放进 result里。
那么为什么使用了vector结构来记录路径呢? 因为在下面处理单层递归逻辑的时候,要做回溯,使用vector方便来做回溯。
可能有的同学问了,我看有些人的代码也没有回溯啊。
其实是有回溯的,只不过隐藏在函数调用时的参数赋值里,下文我还会提到。
这里我们先使用vector结构的path容器来记录路径,那么终止处理逻辑如下:
if (cur-》left == NULL && cur-》right == NULL) { // 遇到叶子节点
string sPath;
for (int i = 0; i 《 path.size() - 1; i++) { // 将path里记录的路径转为string格式
sPath += to_string(path[i]);
sPath += “-》”;
}
sPath += to_string(path[path.size() - 1]); // 记录最后一个节点(叶子节点)
result.push_back(sPath); // 收集一个路径
return;
}
确定单层递归逻辑
因为是前序遍历,需要先处理中间节点,中间节点就是我们要记录路径上的节点,先放进path中。
path.push_back(cur-》val);
然后是递归和回溯的过程,上面说过没有判断cur是否为空,那么在这里递归的时候,如果为空就不进行下一层递归了。
所以递归前要加上判断语句,下面要递归的节点是否为空,如下
if (cur-》left) {
traversal(cur-》left, path, result);
}
if (cur-》right) {
traversal(cur-》right, path, result);
}
此时还没完,递归完,要做回溯啊,因为path 不能一直加入节点,它还要删节点,然后才能加入新的节点。
那么回溯要怎么回溯呢,一些同学会这么写,如下:
if (cur-》left) {
traversal(cur-》left, path, result);
}
if (cur-》right) {
traversal(cur-》right, path, result);
}
path.pop_back();
这个回溯就要很大的问题,我们知道,回溯和递归是一一对应的,有一个递归,就要有一个回溯,这么写的话相当于把递归和回溯拆开了, 一个在花括号里,一个在花括号外。
所以回溯要和递归永远在一起,世界上最遥远的距离是你在花括号里,而我在花括号外!
那么代码应该这么写:
if (cur-》left) {
traversal(cur-》left, path, result);
path.pop_back(); // 回溯
}
if (cur-》right) {
traversal(cur-》right, path, result);
path.pop_back(); // 回溯
}
那么本题整体代码如下:
class Solution {private:
void traversal(TreeNode* cur, vector《int》& path, vector《string》& result) {
path.push_back(cur-》val);
// 这才到了叶子节点
if (cur-》left == NULL && cur-》right == NULL) {
string sPath;
for (int i = 0; i 《 path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += “-》”;
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
return;
}
if (cur-》left) {
traversal(cur-》left, path, result);
path.pop_back(); // 回溯
}
if (cur-》right) {
traversal(cur-》right, path, result);
path.pop_back(); // 回溯
}
}
public:
vector《string》 binaryTreePaths(TreeNode* root) {
vector《string》 result;
vector《int》 path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
如上的C++代码充分体现了回溯。
那么如上代码可以精简成如下代码:
class Solution {private:
void traversal(TreeNode* cur, string path, vector《string》& result) {
path += to_string(cur-》val); // 中
if (cur-》left == NULL && cur-》right == NULL) {
result.push_back(path);
return;
}
if (cur-》left) traversal(cur-》left, path + “-》”, result); // 左
if (cur-》right) traversal(cur-》right, path + “-》”, result); // 右
}
public:
vector《string》 binaryTreePaths(TreeNode* root) {
vector《string》 result;
string path;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
如上代码精简了不少,也隐藏了不少东西。
注意在函数定义的时候void traversal(TreeNode* cur, string path, vector《string》& result) ,定义的是string path,每次都是复制赋值,不用使用引用,否则就无法做到回溯的效果。
那么在如上代码中,貌似没有看到回溯的逻辑,其实不然,回溯就隐藏在traversal(cur-》left, path + “-》”, result);中的 path + “-》”。 每次函数调用完,path依然是没有加上“-》” 的,这就是回溯了。
为了把这份精简代码的回溯过程展现出来,大家可以试一试把:
if (cur-》left) traversal(cur-》left, path + “-》”, result); // 左 回溯就隐藏在这里
改成如下代码:
path += “-》”;
traversal(cur-》left, path, result); // 左
即:
if (cur-》left) {
path += “-》”;
traversal(cur-》left, path, result); // 左
}
if (cur-》right) {
path += “-》”;
traversal(cur-》right, path, result); // 右
}
此时就没有回溯了,这个代码就是通过不了的了。
如果想把回溯加上,就要 在上面代码的基础上,加上回溯,就可以AC了。
if (cur-》left) {
path += “-》”;
traversal(cur-》left, path, result); // 左
path.pop_back(); // 回溯
path.pop_back();
}
if (cur-》right) {
path += “-》”;
traversal(cur-》right, path, result); // 右
path.pop_back(); // 回溯
path.pop_back();
}
大家应该可以感受出来,如果把 path + “-》”作为函数参数就是可以的,因为并有没有改变path的数值,执行完递归函数之后,path依然是之前的数值(相当于回溯了)
综合以上,第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里,第一种递归写法虽然代码多一些,但是把每一个逻辑处理都完整的展现了出来了。
迭代法
至于非递归的方式,我们可以依然可以使用前序遍历的迭代方式来模拟遍历路径的过程,对该迭代方式不了解的同学,可以看文章二叉树:听说递归能做的,栈也能做!和二叉树:前中后序迭代方式统一写法。
这里除了模拟递归需要一个栈,同时还需要一个栈来存放对应的遍历路径。
C++代码如下:
class Solution {public:
vector《string》 binaryTreePaths(TreeNode* root) {
stack《TreeNode*》 treeSt;// 保存树的遍历节点
stack《string》 pathSt; // 保存遍历路径的节点
vector《string》 result; // 保存最终路径集合
if (root == NULL) return result;
treeSt.push(root);
pathSt.push(to_string(root-》val));
while (!treeSt.empty()) {
TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
string path = pathSt.top();pathSt.pop(); // 取出该节点对应的路径
if (node-》left == NULL && node-》right == NULL) { // 遇到叶子节点
result.push_back(path);
}
if (node-》right) { // 右
treeSt.push(node-》right);
pathSt.push(path + “-》” + to_string(node-》right-》val));
}
if (node-》left) { // 左
treeSt.push(node-》left);
pathSt.push(path + “-》” + to_string(node-》left-》val));
}
}
return result;
}
};
当然,使用java的同学,可以直接定义一个成员变量为object的栈Stack《Object》 stack = new Stack《》();,这样就不用定义两个栈了,都放到一个栈里就可以了。
总结
本文我们开始初步涉及到了回溯,很多同学过了这道题目,可能都不知道自己其实使用了回溯,回溯和递归都是相伴相生的。
我在第一版递归代码中,把递归与回溯的细节都充分的展现了出来,大家可以自己感受一下。
第二版递归代码对于初学者其实非常不友好,代码看上去简单,但是隐藏细节于无形。
最后我依然给出了迭代法。
对于本地充分了解递归与回溯的过程之后,有精力的同学可以在去实现迭代法。
其他语言版本
Java:
//解法一class Solution {
/**
* 递归法
*/
public List《String》 binaryTreePaths(TreeNode root) {
List《String》 res = new ArrayList《》();
if (root == null) {
return res;
}
List《Integer》 paths = new ArrayList《》();
traversal(root, paths, res);
return res;
}
private void traversal(TreeNode root, List《Integer》 paths, List《String》 res) {
paths.add(root.val);
// 叶子结点
if (root.left == null && root.right == null) {
// 输出
StringBuilder sb = new StringBuilder();
for (int i = 0; i 《 paths.size() - 1; i++) {
sb.append(paths.get(i)).append(“-》”);
}
sb.append(paths.get(paths.size() - 1));
res.add(sb.toString());
return;
}
if (root.left != null) {
traversal(root.left, paths, res);
paths.remove(paths.size() - 1);// 回溯
}
if (root.right != null) {
traversal(root.right, paths, res);
paths.remove(paths.size() - 1);// 回溯
}
}
}
class Solution:
def binaryTreePaths(self, root: TreeNode) -》 List[str]:
path=[]
res=[]
def backtrace(root, path):
if not root:return
path.append(root.val)
if (not root.left)and (not root.right):
res.append(path[:])
ways=[]
if root.left:ways.append(root.left)
if root.right:ways.append(root.right)
for way in ways:
backtrace(way,path)
path.pop()
backtrace(root,path)
return [“-》”.join(list(map(str,i))) for i in res]
Go:
func binaryTreePaths(root *TreeNode) []string {
res := make([]string, 0)
var travel func(node *TreeNode, s string)
travel = func(node *TreeNode, s string) {
if node.Left == nil && node.Right == nil {
v := s + strconv.Itoa(node.Val)
res = append(res, v)
return
}
s = s + strconv.Itoa(node.Val) + “-》”
if node.Left != nil {
travel(node.Left, s)
}
if node.Right != nil {
travel(node.Right, s)
}
}
travel(root, “”)
return res
}
责任编辑:haq
-
函数
+关注
关注
3文章
4352浏览量
63247 -
二叉树
+关注
关注
0文章
74浏览量
12424
原文标题:二叉树的所有路径:不止递归,还有回溯
文章出处:【微信号:xincailiaozaixian,微信公众号:新材料在线】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
机器人看点:宇树科技王兴兴回上海母校 加速商业化落地 宇树机器人二手租赁火爆
宇树科技在物联网方面
FRED应用:二阶鬼像分析
嵌入式学习-飞凌嵌入式ElfBoard ELF 1板卡-初识设备树之设备树组成和结构
飞凌嵌入式ElfBoard ELF 1板卡-初识设备树之设备树组成和结构
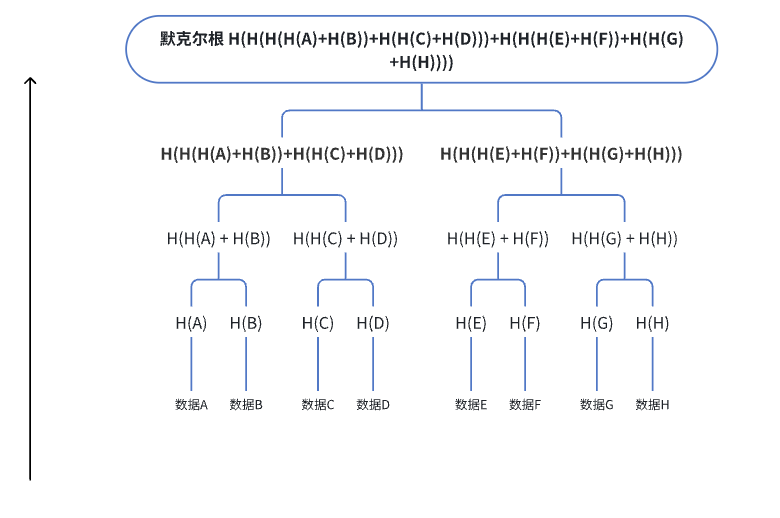
什么是默克尔树(Merkle Tree)?如何计算默克尔根?
INA228-Q1防反接设计遇到的疑问求解
请问3个esp32_Devkitc_v4模块再没有路由器的情况下怎么各自互联
多叉指MOSFET器件静电防护鲁棒性提升技巧
原理图设计里两颗重要的树(国产EDA)
圣诞树灯电路图分享




 二叉树的所有路径介绍
二叉树的所有路径介绍











评论