本期是C++基础语法分享的第十四节,今天给大家来梳理一下树!
二叉树
BinaryTree.cpp:
#include 《stdio.h》#include 《stdlib.h》
#define TRUE 1#define FALSE 0#define OK 1#define ERROR 0#define OVERFLOW -1#define SUCCESS 1#define UNSUCCESS 0#define dataNum 5int i = 0;int dep = 0;char data[dataNum] = { ‘A’, ‘B’, ‘C’, ‘D’, ‘E’ };
typedef int Status;typedef char TElemType;
// 二叉树结构typedef struct BiTNode{ TElemType data; struct BiTNode *lchild, *rchild;}BiTNode, *BiTree;
// 初始化一个空树void InitBiTree(BiTree &T){ T = NULL;}
// 构建二叉树BiTree MakeBiTree(TElemType e, BiTree L, BiTree R){ BiTree t; t = (BiTree)malloc(sizeof(BiTNode)); if (NULL == t) return NULL; t-》data = e; t-》lchild = L; t-》rchild = R; return t;}
// 访问结点Status visit(TElemType e){ printf(“%c”, e); return OK;}
// 对二叉树T求叶子结点数目int Leaves(BiTree T){ int l = 0, r = 0; if (NULL == T) return 0; if (NULL == T-》lchild && NULL == T-》rchild) return 1;
// 求左子树叶子数目 l = Leaves(T-》lchild); // 求右子树叶子数目 r = Leaves(T-》rchild); // 组合 return r + l;}
// 层次遍历:dep是个全局变量,高度int depTraverse(BiTree T){ if (NULL == T) return ERROR;
dep = (depTraverse(T-》lchild) 》 depTraverse(T-》rchild)) ? depTraverse(T-》lchild) : depTraverse(T-》rchild);
return dep + 1;}
// 高度遍历:lev是局部变量,层次void levTraverse(BiTree T, Status(*visit)(TElemType e), int lev){ if (NULL == T) return; visit(T-》data); printf(“的层次是%d
”, lev);
levTraverse(T-》lchild, visit, ++lev); levTraverse(T-》rchild, visit, lev);}
// num是个全局变量void InOrderTraverse(BiTree T, Status(*visit)(TElemType e), int &num){ if (NULL == T) return; visit(T-》data); if (NULL == T-》lchild && NULL == T-》rchild) { printf(“是叶子结点”); num++; } else printf(“不是叶子结点”); printf(“
”); InOrderTraverse(T-》lchild, visit, num); InOrderTraverse(T-》rchild, visit, num);}
// 二叉树判空Status BiTreeEmpty(BiTree T){ if (NULL == T) return TRUE; return FALSE;}
// 打断二叉树:置空二叉树的左右子树Status BreakBiTree(BiTree &T, BiTree &L, BiTree &R){ if (NULL == T) return ERROR; L = T-》lchild; R = T-》rchild; T-》lchild = NULL; T-》rchild = NULL; return OK;}
// 替换左子树Status ReplaceLeft(BiTree &T, BiTree <){ BiTree temp; if (NULL == T) return ERROR; temp = T-》lchild; T-》lchild = LT; LT = temp; return OK;}
// 替换右子树Status ReplaceRight(BiTree &T, BiTree &RT){ BiTree temp; if (NULL == T) return ERROR; temp = T-》rchild; T-》rchild = RT; RT = temp; return OK;}
// 合并二叉树void UnionBiTree(BiTree &Ttemp){ BiTree L = NULL, R = NULL; L = MakeBiTree(data[i++], NULL, NULL); R = MakeBiTree(data[i++], NULL, NULL); ReplaceLeft(Ttemp, L); ReplaceRight(Ttemp, R);}
int main(){ BiTree T = NULL, Ttemp = NULL;
InitBiTree(T); if (TRUE == BiTreeEmpty(T)) printf(“初始化T为空
”); else printf(“初始化T不为空
”);
T = MakeBiTree(data[i++], NULL, NULL);
Ttemp = T; UnionBiTree(Ttemp);
Ttemp = T-》lchild; UnionBiTree(Ttemp);
Status(*visit1)(TElemType); visit1 = visit; int num = 0; InOrderTraverse(T, visit1, num); printf(“叶子结点是 %d
”, num);
printf(“叶子结点是 %d
”, Leaves(T));
int lev = 1; levTraverse(T, visit1, lev);
printf(“高度是 %d
”, depTraverse(T));
getchar(); return 0;}
性质
(1)非空二叉树第 i 层最多 2(i-1) 个结点 (i 》= 1)
(2)深度为 k 的二叉树最多 2k - 1 个结点 (k 》= 1)
(3)度为 0 的结点数为 n0,度为 2 的结点数为 n2,则 n0 = n2 + 1
(4)有 n 个结点的完全二叉树深度 k = ⌊ log2(n) ⌋ + 1
(5)对于含 n 个结点的完全二叉树中编号为 i (1 《= i 《= n) 的结点
a.若 i = 1,为根,否则双亲为 ⌊ i / 2 ⌋
b.若 2i 》 n,则 i 结点没有左孩子,否则孩子编号为 2i
c.若 2i + 1 》 n,则 i 结点没有右孩子,否则孩子编号为 2i + 1
存储结构
二叉树数据结构
typedef struct BiTNode{ TElemType data; struct BiTNode *lchild, *rchild;}BiTNode, *BiTree;
顺序存储
二叉树顺序存储图片
链式存
二叉树链式存储图片
遍历方式
a.先序遍历
b.中序遍历
c.后续遍历
d.层次遍历
分类
(1)满二叉树
(2)完全二叉树(堆)
大顶堆:根 》= 左 && 根 》= 右
小顶堆:根 《= 左 && 根 《= 右
(3)二叉查找树(二叉排序树):左 《 根 《 右
(4)平衡二叉树(AVL树):| 左子树树高 - 右子树树高 | 《= 1
(5)最小失衡树:平衡二叉树插入新结点导致失衡的子树:调整:
LL型:根的左孩子右旋
RR型:根的右孩子左旋
LR型:根的左孩子左旋,再右旋
RL型:右孩子的左子树,先右旋,再左旋
其他树及森林
1、树的存储结构
(1)双亲表示法
(2)双亲孩子表示法
(3)孩子兄弟表示法
并查集
一种不相交的子集所构成的集合 S = {S1, S2, 。.., Sn}
2、平衡二叉树(AVL树)
性质
(1)| 左子树树高 - 右子树树高 | 《= 1
(2)平衡二叉树必定是二叉搜索树,反之则不一定
(3)最小二叉平衡树的节点的公式:F(n)=F(n-1)+F(n-2)+1 (1 是根节点,F(n-1) 是左子树的节点数量,F(n-2) 是右子树的节点数量)
平衡二叉树图片
最小失衡树
平衡二叉树插入新结点导致失衡的子树
调整:
LL 型:根的左孩子右旋
RR 型:根的右孩子左旋
LR 型:根的左孩子左旋,再右旋
RL 型:右孩子的左子树,先右旋,再左旋
3、红黑树
RedBlackTree.cpp:
#define BLACK 1#define RED 0#include 《iostream》
using namespace std;
class bst {private:
struct Node { int value; bool color; Node *leftTree, *rightTree, *parent;
Node() : value(0), color(RED), leftTree(NULL), rightTree(NULL), parent(NULL) { }
Node* grandparent() { if (parent == NULL) { return NULL; } return parent-》parent; }
Node* uncle() { if (grandparent() == NULL) { return NULL; } if (parent == grandparent()-》rightTree) return grandparent()-》leftTree; else return grandparent()-》rightTree; }
Node* sibling() { if (parent-》leftTree == this) return parent-》rightTree; else return parent-》leftTree; } };
void rotate_right(Node *p) { Node *gp = p-》grandparent(); Node *fa = p-》parent; Node *y = p-》rightTree;
fa-》leftTree = y;
if (y != NIL) y-》parent = fa; p-》rightTree = fa; fa-》parent = p;
if (root == fa) root = p; p-》parent = gp;
if (gp != NULL) { if (gp-》leftTree == fa) gp-》leftTree = p; else gp-》rightTree = p; }
}
void rotate_left(Node *p) { if (p-》parent == NULL) { root = p; return; } Node *gp = p-》grandparent(); Node *fa = p-》parent; Node *y = p-》leftTree;
fa-》rightTree = y;
if (y != NIL) y-》parent = fa; p-》leftTree = fa; fa-》parent = p;
if (root == fa) root = p; p-》parent = gp;
if (gp != NULL) { if (gp-》leftTree == fa) gp-》leftTree = p; else gp-》rightTree = p; } }
void inorder(Node *p) { if (p == NIL) return;
if (p-》leftTree) inorder(p-》leftTree);
cout 《《 p-》value 《《 “ ”;
if (p-》rightTree) inorder(p-》rightTree); }
string outputColor(bool color) { return color ? “BLACK” : “RED”; }
Node* getSmallestChild(Node *p) { if (p-》leftTree == NIL) return p; return getSmallestChild(p-》leftTree); }
bool delete_child(Node *p, int data) { if (p-》value 》 data) { if (p-》leftTree == NIL) { return false; } return delete_child(p-》leftTree, data); } else if (p-》value 《 data) { if (p-》rightTree == NIL) { return false; } return delete_child(p-》rightTree, data); } else if (p-》value == data) { if (p-》rightTree == NIL) { delete_one_child(p); return true; } Node *smallest = getSmallestChild(p-》rightTree); swap(p-》value, smallest-》value); delete_one_child(smallest);
return true; } else { return false; } }
void delete_one_child(Node *p) { Node *child = p-》leftTree == NIL ? p-》rightTree : p-》leftTree; if (p-》parent == NULL && p-》leftTree == NIL && p-》rightTree == NIL) { p = NULL; root = p; return; }
if (p-》parent == NULL) { delete p; child-》parent = NULL; root = child; root-》color = BLACK; return; }
if (p-》parent-》leftTree == p) { p-》parent-》leftTree = child; } else { p-》parent-》rightTree = child; } child-》parent = p-》parent;
if (p-》color == BLACK) { if (child-》color == RED) { child-》color = BLACK; } else delete_case(child); }
delete p; }
void delete_case(Node *p) { if (p-》parent == NULL) { p-》color = BLACK; return; } if (p-》sibling()-》color == RED) { p-》parent-》color = RED; p-》sibling()-》color = BLACK; if (p == p-》parent-》leftTree) rotate_left(p-》sibling()); else rotate_right(p-》sibling()); } if (p-》parent-》color == BLACK && p-》sibling()-》color == BLACK && p-》sibling()-》leftTree-》color == BLACK && p-》sibling()-》rightTree-》color == BLACK) { p-》sibling()-》color = RED; delete_case(p-》parent); } else if (p-》parent-》color == RED && p-》sibling()-》color == BLACK && p-》sibling()-》leftTree-》color == BLACK && p-》sibling()-》rightTree-》color == BLACK) { p-》sibling()-》color = RED; p-》parent-》color = BLACK; } else { if (p-》sibling()-》color == BLACK) { if (p == p-》parent-》leftTree && p-》sibling()-》leftTree-》color == RED && p-》sibling()-》rightTree-》color == BLACK) { p-》sibling()-》color = RED; p-》sibling()-》leftTree-》color = BLACK; rotate_right(p-》sibling()-》leftTree); } else if (p == p-》parent-》rightTree && p-》sibling()-》leftTree-》color == BLACK && p-》sibling()-》rightTree-》color == RED) { p-》sibling()-》color = RED; p-》sibling()-》rightTree-》color = BLACK; rotate_left(p-》sibling()-》rightTree); } } p-》sibling()-》color = p-》parent-》color; p-》parent-》color = BLACK; if (p == p-》parent-》leftTree) { p-》sibling()-》rightTree-》color = BLACK; rotate_left(p-》sibling()); } else { p-》sibling()-》leftTree-》color = BLACK; rotate_right(p-》sibling()); } } }
void insert(Node *p, int data) { if (p-》value 》= data) { if (p-》leftTree != NIL) insert(p-》leftTree, data); else { Node *tmp = new Node(); tmp-》value = data; tmp-》leftTree = tmp-》rightTree = NIL; tmp-》parent = p; p-》leftTree = tmp; insert_case(tmp); } } else { if (p-》rightTree != NIL) insert(p-》rightTree, data); else { Node *tmp = new Node(); tmp-》value = data; tmp-》leftTree = tmp-》rightTree = NIL; tmp-》parent = p; p-》rightTree = tmp; insert_case(tmp); } } }
void insert_case(Node *p) { if (p-》parent == NULL) { root = p; p-》color = BLACK; return; } if (p-》parent-》color == RED) { if (p-》uncle()-》color == RED) { p-》parent-》color = p-》uncle()-》color = BLACK; p-》grandparent()-》color = RED; insert_case(p-》grandparent()); } else { if (p-》parent-》rightTree == p && p-》grandparent()-》leftTree == p-》parent) { rotate_left(p); rotate_right(p); p-》color = BLACK; p-》leftTree-》color = p-》rightTree-》color = RED; } else if (p-》parent-》leftTree == p && p-》grandparent()-》rightTree == p-》parent) { rotate_right(p); rotate_left(p); p-》color = BLACK; p-》leftTree-》color = p-》rightTree-》color = RED; } else if (p-》parent-》leftTree == p && p-》grandparent()-》leftTree == p-》parent) { p-》parent-》color = BLACK; p-》grandparent()-》color = RED; rotate_right(p-》parent); } else if (p-》parent-》rightTree == p && p-》grandparent()-》rightTree == p-》parent) { p-》parent-》color = BLACK; p-》grandparent()-》color = RED; rotate_left(p-》parent); } } } }
void DeleteTree(Node *p) { if (!p || p == NIL) { return; } DeleteTree(p-》leftTree); DeleteTree(p-》rightTree); delete p; }public:
bst() { NIL = new Node(); NIL-》color = BLACK; root = NULL; }
~bst() { if (root) DeleteTree(root); delete NIL; }
void inorder() { if (root == NULL) return; inorder(root); cout 《《 endl; }
void insert(int x) { if (root == NULL) { root = new Node(); root-》color = BLACK; root-》leftTree = root-》rightTree = NIL; root-》value = x; } else { insert(root, x); } }
bool delete_value(int data) { return delete_child(root, data); }private: Node *root, *NIL;};
int main(){ cout 《《 “---【红黑树】---” 《《 endl; // 创建红黑树 bst tree;
// 插入元素 tree.insert(2); tree.insert(9); tree.insert(-10); tree.insert(0); tree.insert(33); tree.insert(-19);
// 顺序打印红黑树 cout 《《 “插入元素后的红黑树:” 《《 endl; tree.inorder();
// 删除元素 tree.delete_value(2);
// 顺序打印红黑树 cout 《《 “删除元素 2 后的红黑树:” 《《 endl; tree.inorder();
// 析构 tree.~bst();
getchar(); return 0;}
红黑树的特征是什么?
(1)节点是红色或黑色。
(2)根是黑色。
(3)所有叶子都是黑色(叶子是 NIL 节点)。
(4)每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)(新增节点的父节点必须相同)
(5)从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。(新增节点必须为红)
调整
(1)变色
(2)左旋
(3)右旋
应用
关联数组:如 STL 中的 map、set
红黑树、B 树、B+ 树的区别?
(1)红黑树的深度比较大,而 B 树和 B+ 树的深度则相对要小一些
(2)B+ 树则将数据都保存在叶子节点,同时通过链表的形式将他们连接在一起。
B 树(B-tree)、B+ 树(B+-tree)
特点
一般化的二叉查找树(binary search tree)
“矮胖”,内部(非叶子)节点可以拥有可变数量的子节点(数量范围预先定义好)
应用
大部分文件系统、数据库系统都采用B树、B+树作为索引结构
区别
B+树中只有叶子节点会带有指向记录的指针(ROWID),而B树则所有节点都带有,在内部节点出现的索引项不会再出现在叶子节点中。
B+树中所有叶子节点都是通过指针连接在一起,而B树不会。
B树的优点
对于在内部节点的数据,可直接得到,不必根据叶子节点来定位。
B+树的优点
非叶子节点不会带上 ROWID,这样,一个块中可以容纳更多的索引项,一是可以降低树的高度。二是一个内部节点可以定位更多的叶子节点。
叶子节点之间通过指针来连接,范围扫描将十分简单,而对于B树来说,则需要在叶子节点和内部节点不停的往返移动。
B 树、B+ 树区别来自:differences-between-b-trees-and-b-trees、B树和B+树的区别
八叉树
八叉树图片
八叉树(octree),或称八元树,是一种用于描述三维空间(划分空间)的树状数据结构。八叉树的每个节点表示一个正方体的体积元素,每个节点有八个子节点,这八个子节点所表示的体积元素加在一起就等于父节点的体积。一般中心点作为节点的分叉中心。
用途
三维计算机图形
最邻近搜索
责任编辑:haq
-
数据
+关注
关注
8文章
7067浏览量
89107 -
C++
+关注
关注
22文章
2110浏览量
73685 -
二叉树
+关注
关注
0文章
74浏览量
12338
原文标题:C++基础语法梳理:数据结构丨树(二叉树和红黑树)
文章出处:【微信号:cyuyanxuexi,微信公众号:C语言编程学习基地】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
AKI跨语言调用库神助攻C/C++代码迁移至HarmonyOS NEXT
同样是函数,在C和C++中有什么区别
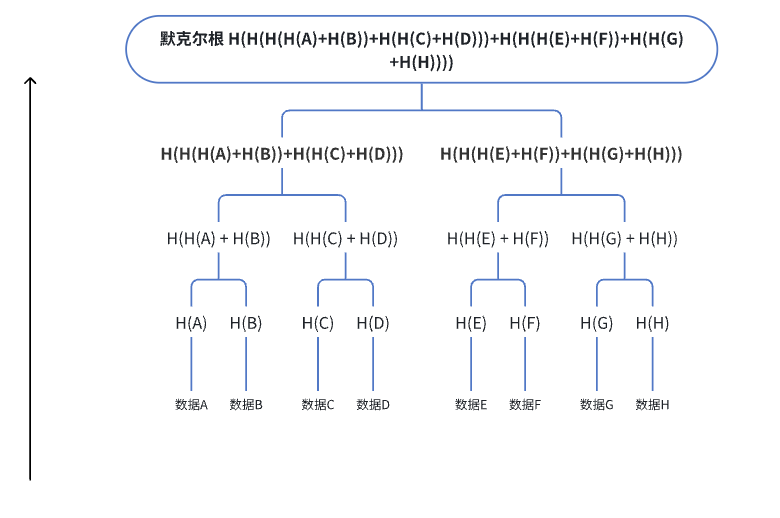
什么是默克尔树(Merkle Tree)?如何计算默克尔根?
ostream在c++中的用法
C/C++中两种宏实现方式
鸿蒙OS开发实例:【Native C++】
使用 MISRA C++:2023® 避免基于范围的 for 循环中的错误





 C++基础语法中的二叉树详解
C++基础语法中的二叉树详解











评论