傅里叶变换的公式为:
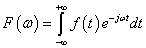
可以把傅里叶变换也成另外一种形式:
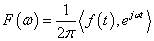
可以看出,傅里叶变换的本质是内积,三角函数是完备的正交函数集,不同频率的三角函数的之间的内积为0,只有频率相等的三角函数做内积时,才不为0。
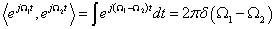
下面从公式解释下傅里叶变换的意义
因为傅里叶变换的本质是内积,所以f(t)和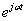 求内积的时候,只有f(t)中频率为ω的分量才会有内积的结果,其余分量的内积为0。可以理解为f(t)在
求内积的时候,只有f(t)中频率为ω的分量才会有内积的结果,其余分量的内积为0。可以理解为f(t)在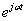 上的投影,积分值是时间从负无穷到正无穷的积分,就是把信号每个时间在ω的分量叠加起来,可以理解为f(t)在
上的投影,积分值是时间从负无穷到正无穷的积分,就是把信号每个时间在ω的分量叠加起来,可以理解为f(t)在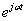 上的投影的叠加,叠加的结果就是频率为ω的分量,也就形成了频谱。
上的投影的叠加,叠加的结果就是频率为ω的分量,也就形成了频谱。
傅里叶逆变换的公式为:
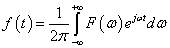
下面从公式分析下傅里叶逆变换的意义
傅里叶逆变换就是傅里叶变换的逆过程,在F(ω)和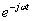 求内积的时候,F(ω)只有t时刻的分量内积才会有结果,其余时间分量内积结果为0,同样积分值是频率从负无穷到正无穷的积分,就是把信号在每个频率在t时刻上的分量叠加起来,叠加的结果就是f(t)在t时刻的值,这就回到了我们观察信号最初的时域。
求内积的时候,F(ω)只有t时刻的分量内积才会有结果,其余时间分量内积结果为0,同样积分值是频率从负无穷到正无穷的积分,就是把信号在每个频率在t时刻上的分量叠加起来,叠加的结果就是f(t)在t时刻的值,这就回到了我们观察信号最初的时域。
对一个信号做傅里叶变换,然后直接做逆变换,这样做是没有意义的,在傅里叶变换和傅里叶逆变换之间有一个滤波的过程。将不要的频率分量给滤除掉,然后再做逆变换,就得到了想要的信号。比如信号中掺杂着噪声信号,可以通过滤波器将噪声信号的频率给去除,再做傅里叶逆变换,就得到了没有噪声的信号。
优点:频率的定位很好,通过对信号的频率分辨率很好,可以清晰的得到信号所包含的频率成分,也就是频谱。
缺点:因为频谱是时间从负无穷到正无穷的叠加,所以,知道某一频率,不能判断,该频率的时间定位。不能判断某一时间段的频率成分。
例子:
平稳信号:
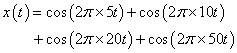
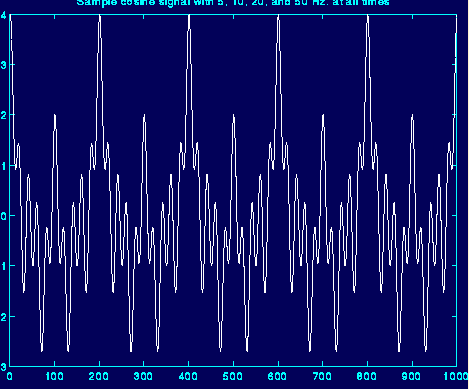
傅里叶变换的结果:
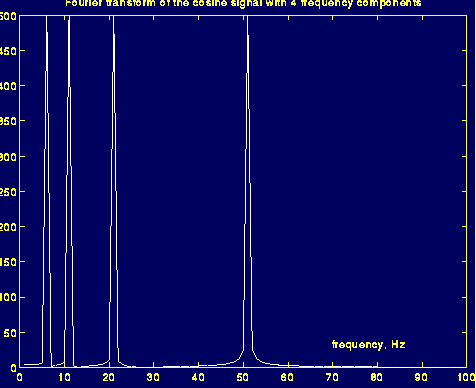
由于信号是平稳信号,每处的频率都相等,所以看不到傅里叶变换的缺点。
对于非平稳信号:信号是余弦信号,仍然有四个频率分量
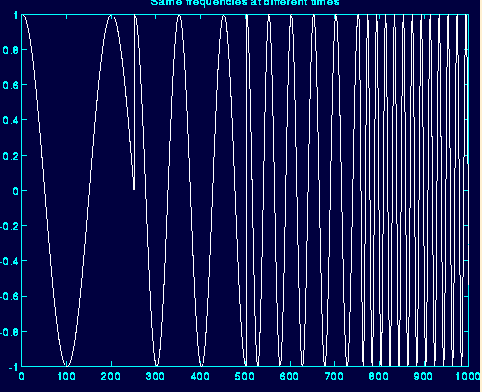
傅里叶变换的结果:
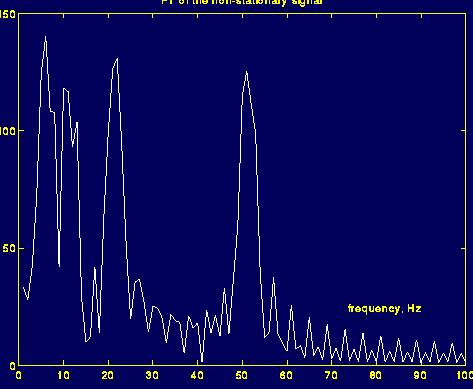
由上图看出知道某一频率,不能判断,该频率的时间定位。不能判断某一时间段的频率成分。
短时傅里叶变换
傅里叶变换存在着严重的缺点,就是不能实现时频联合分析。傅里叶变换要从负无穷计算到正无穷,这在实际使用当中,跟即时性分析会有很大的矛盾。根据这一缺点,提出了短时傅里叶变换。后来的时间—频率分析也是以短时傅里叶变换为基础提出的。
为了弥补傅里叶变换的缺陷,给信号加上一个窗函数,对信号加窗后计算加窗后函数的傅里叶变换,加窗后得到时间附近的很小时间上的局部谱,窗函数可以根据时间的位置变化在整个时间轴上平移,利用窗函数可以得到任意位置附近的时间段频谱,实现了时间局域化。
短时傅里叶变换的公式为:
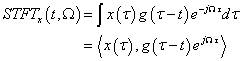
在时域用窗函数去截信号,对截下来的局部信号作傅立叶变换,即在t时刻得该段信号得傅立叶变换,不断地移动t,也即不断地移动窗函数的中心位置,即可得到不同时刻的傅立叶变换,这样就得到了时间—频率分析。
短时傅里叶变换的本质和傅里叶变换一样都是内积,只不过用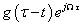 代替了
代替了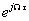 ,实现了局部信号的频谱分析。
,实现了局部信号的频谱分析。
短时傅里叶变换的另一种形式:
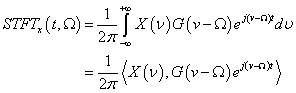
该式子表明在时域里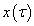 加窗函数
加窗函数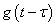 ,得出在频域里对
,得出在频域里对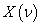 加窗
加窗 。
。
优点:在傅里叶变换的基础上,增加了窗函数,就实现了时间—频率分析。
缺点:短时傅里叶变换使用一个固定的窗函数,窗函数一旦确定了以后,其形状就不再发生改变,短时傅里叶变换的分辨率也就确定了。如果要改变分辨率,则需要重新选择窗函数。短时傅里叶变换用来分析分段平稳信号或者近似平稳信号犹可,但是对于非平稳信号,当信号变化剧烈时,要求窗函数有较高的时间分辨率;而波形变化比较平缓的时刻,主要是低频信号,则要求窗函数有较高的频率分辨率。短时傅里叶变换不能兼顾频率与时间分辨率的需求。测不准原理告诉我们,不可能在时间和频率两个空间同时以任意精度逼近被测信号,因此就必须在信号的分析上对时间或者频率的精度做取舍。短时傅里叶变换受到测不准原理的限制,所以短时傅里叶变换窗函数的时间与频率分辨率不能同时达到最优。在实际使用时,根据实际情况选用合适的窗函数。
例子:
原始信号:信号是余弦信号,有四个频率分量.

当窗函数选为:
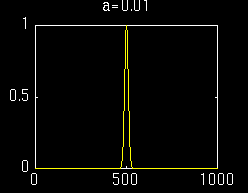
短时傅里叶变换为:

由上图可以看出,时域的分辨率比较好,但是频率出现一定宽度的带宽,也就是说频率分辨率差;
当窗函数选择为:
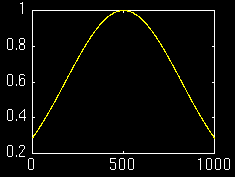
短时傅里叶变换为:
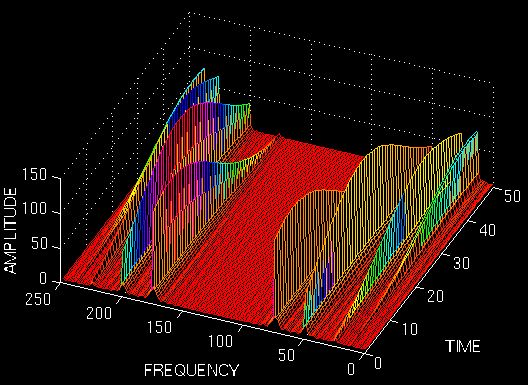
由上图可以看出,频率的分辨率比较好,但是时域分辨率差,有点接近傅里叶变换。由上图可以看到短时傅里叶变换的缺点。
审核编辑 :李倩
-
频率
+关注
关注
4文章
1500浏览量
59227 -
傅里叶变换
+关注
关注
6文章
441浏览量
42600
原文标题:一文道破傅里叶变换的本质,优缺点一目了然
文章出处:【微信号:EMC_EMI,微信公众号:电磁兼容EMC】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
一文道破傅里叶变换的本质,优缺点一目了然
学习傅里叶变换意义和方法
傅里叶变换意义是什么
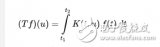
傅里叶变换的介绍傅里叶变换有什么意义和应用





 傅里叶变换的意义
傅里叶变换的意义










评论