时间序列分析的定义

01

时间序列分析的定义

1.1

概念

首先，时间序列定义为在一定时间间隔内按时间顺序测量的某个数量。时间序列分析是指将历史数据分解为四部分来看——趋势、周期、时期和不稳定因素，然后综合这些因素，提出预测。时间序列分为平稳序列和非平稳序列两大类。平稳序列是不存在趋势只存在随机性的序列，非平稳序列则是包含趋势、季节性和随机性的序列。

从最广泛的形式来说，时间序列分析是关于推断过去一系列数据点发生了什么，并试图预测未来会发生什么。时间序列分析试图了解过去并预测未来。

1.2

分类

通常，时间序列通常包含以下类型：

1、趋势-趋势是时间序列中一致的方向性运动。这些趋势将是确定性的或随机的。时间序列在长时间内呈现出来的长期上升或下降的变动；

2、季节性变化-许多时间序列都包含季节性变化。在代表业务销售或气候水平的系列中尤其如此。我们经常看到商品的季节性变化，特别是那些与生长季节或年度温度变化有关的商品（例如天然气）。

3、序列依赖性-时间序列（尤其是金融序列）最重要的特征之一就是序列相关性。当时间上相互靠近的时间序列观测值倾向于相互关联时，就会发生这种情况。

02

时间序列分析的步骤

时间序列预测的步骤是：

在开始平稳性检验步骤之前，我首先想和大家分享的是平稳性检验的目的。平稳性检验为了确定没有随机趋势或确定趋势,否则将会产生“伪回归”问题.伪回归是说,有时数据的高度相关仅仅是因为二者同时随时间有向上或向下的变动趋势, 并没有真正联系.这样数据中的趋势项,季节项等无法消除, 从而在残差分析中无法准确进行分析。

2.1

平稳性检验

（一）图示法

平稳性指的是期望不变，方差恒定，协方差不随时间改变，协方差只依赖于K这个时间跨度，不依赖于时间点t本身。

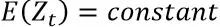
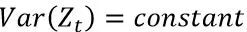
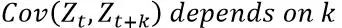
给定这些假设前提的目的是便于后续技术上的处理。根据时序图粗略来判断序列是否平稳，平稳时序图的特征为围绕均值不断波动，而非平稳时序图表现为在不同时间段具有不同的均值。图a为平稳时序图，图b为非平稳时序图。

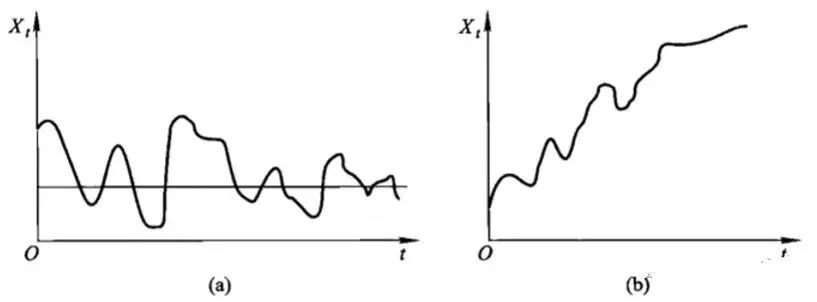
然而仅依靠图像判断时间序列的平稳性，肯定是不精确的，因此需要进行单位根检验（DF检验和ADF检验）进一步判断。

（二）单位根检验

1、DF检验

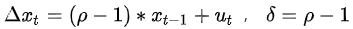
（原假设 H0：序存在单位根 ，即参数δ=0）

检验时间序列的平稳性，一般可通过检验带有截距项的一阶自回归模型：

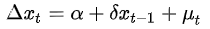
对上式可通过进行普通最小二乘法的t检验完成（t检验的原假设：H0：βj=0。即若P值<0.05，则拒绝原假设，证明δ≠0，序列平稳。

2、ADF检验 因DF检验假设ut为白噪声，序列为一阶自回归的模型，但实际上随机干扰项并非为白噪声序列，且序列并非为一阶自回归生成，因此用普通最小二乘法进行估计的t统计量会受到无关参数的影响，导致DF检验无效。

如果时间序列包含有明显的随时间变化的某种趋势，DF检验必须保证能够剔除这种趋势，否则时间趋势的成分会进入ut，导致ut非白噪声序列，进而偏离了最初的假设。因此形成了ADF检验。ADF检验是由下面3个模型完成：

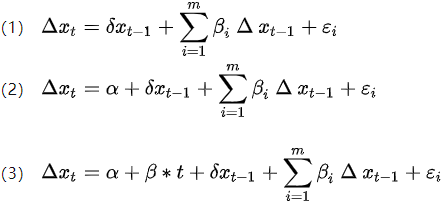
其中t为时间变量，代表序列随时间变化的趋势。

模型的检验原理同DF检验，即t检验；检验顺序为（3）、（2）、（1）；三个模型全部检验通过，才能证明该序列是平稳时间序列。

2.2

时间序列常见的三种模型

序列通过平稳性检验后，就可以建立时间序列模型了，当序列不平稳时，对序列进行差分或者取对数处理。对时序数据进行差分处理，例如在R语言的“diff”函数可确定（P值<0.05，则拒绝原假设，序列不存在单位根，经1阶差分后，序列平稳）。

对一个时间序列预处理后检验出该序列为平稳时间序列说明该模型有提取信息的价值，就要进行下一步的模型建立来拟合该模型然后做出预测。下面介绍拟合时间序列的三个重要模型。

（一）AR(p)模型

自回归模型(Autoregressive model，简称AR模型)，用同一变数例如x的之前各期，亦即x1至xt-1来预测本期xt的表现，并假设它们为一次线性关系。因为这是从回归分析中的线性回归发展而来，只是不用x预测y，而是用x预测 x（自己）；所以叫做自回归。

AR(p)模型简记形式如下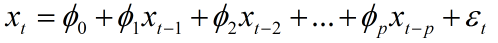： 其中p为自回归阶数。Φ0=0称为中心化AR(p)模型。p阶自回归模型的自相关系数拖尾，偏自相关系数p阶截尾。

（二）MA(q)模型 MA模型(moving average model)移动平均模型，简记形式如下：

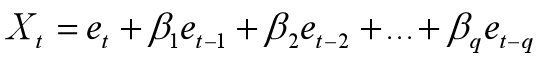
其中q为移动平均的阶数。q阶移动平均模型自相关系数q阶截尾，偏自相关系数拖尾。

（三）ARMA(p,q)模型 自回归滑动平均模型(Autoregressive moving average model，简称：ARMA模型)。是研究时间序列的重要方法，由自回归模型（简称AR模型）与移动平均模型（简称MA模型）为基础“混合”构成。它比AR模型法与MA模型法估计更精确，但其参数估算比较繁琐。ARMA(p,q)模型简记形式如下：

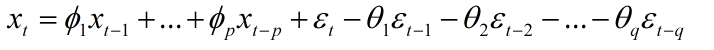
当q=0时，ARMA(p,q)模型就退化成了AR(p)模型；

当p=0时，ARMA(p,q)模型就退化成了MA(q)模型；

ARMA(p,q)模型具有自相关系数不截尾，偏自相关系数也不截尾的性质。

2.3

模型的选择与定阶

了解了时间序列的三种常见模型后，应该如何选择模型并确定模型的阶数呢？通常使用ACF与PACF图判定法。

说到时间序列分析，一定离不开自相关函数(auto-correlation function，ACF)和偏自相关函数(Partial auto-correlation function，PACF)，ACF可以提供具有滞后值的任何序列的自相关值。

简单来说，它描述了该序列的当前值与其过去的值之间的相关程度。时间序列可以包含趋势，季节性，周期性和残差等成分。ACF在寻找相关性时会考虑所有这些成分。直观上来说，ACF 描述了一个观测值和另一个观测值之间的自相关，包括直接和间接的相关性信息。

PACF可以提供残差（在去除了之前的滞后已经解释的影响之后仍然存在）与下一个滞后值的相关性。因此，如果残差中有任何可以由下一个滞后建模的隐藏信息，我们可能会获得良好的相关性，并且在建模时我们会将下一个滞后作为特征。

讨论完两个重要函数后，就成功了一半，接下来就是选择模型和确定阶数了，由此引入两个词：截尾和拖尾。

截尾是指时间序列的自相关函数（ACF）或偏自相关函数（PACF）在大于某个常数k后快速趋于0为k阶截尾；拖尾是ACF或PACF始终有非零取值，不会在k大于某个常数后就恒等于零(或在0附近随机波动)。趋于0在实际分析过程中通常被处理为在2倍标准差之内。

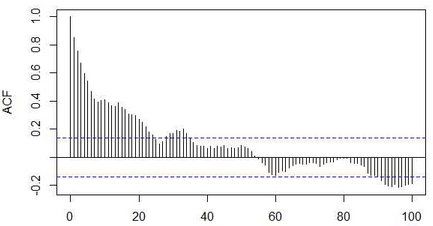
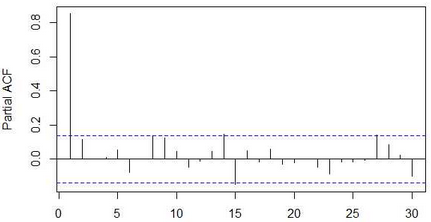
以上面两张图为例，ACF拖尾，PACF一阶截尾，因此可以选择AR(1)模型进行拟合，说到模型拟合，各位统计学前辈早已为我们总结好以下规律：

2.4

模型的确定与检验

通过以上内容，大家对时间序列的三种模型有了初步了解。那么应该如何确定最优模型呢？通常有以下几点：

（1）同一种模型，在尽可能描述数据信息的前提下选择低阶模型，阶数越高，模型会越复杂

（2）高阶AR(p)、MA(q)模型与较低阶ARMA(p,q)模型之间选择较低阶ARMA(p,q)模型

（3）合适模型的残差应满足均值为零的正态分布，而且任何滞后阶数的残差相关系数都为零。

接下来分享的是残差检验的方法：

方法一：通过绘制正态分布的QQ来检验：图像近似为过原点的一条直线，则残差服从正态分布且均值为零。该步骤可通过R语言的“qqnormt”函数实现。如下图：

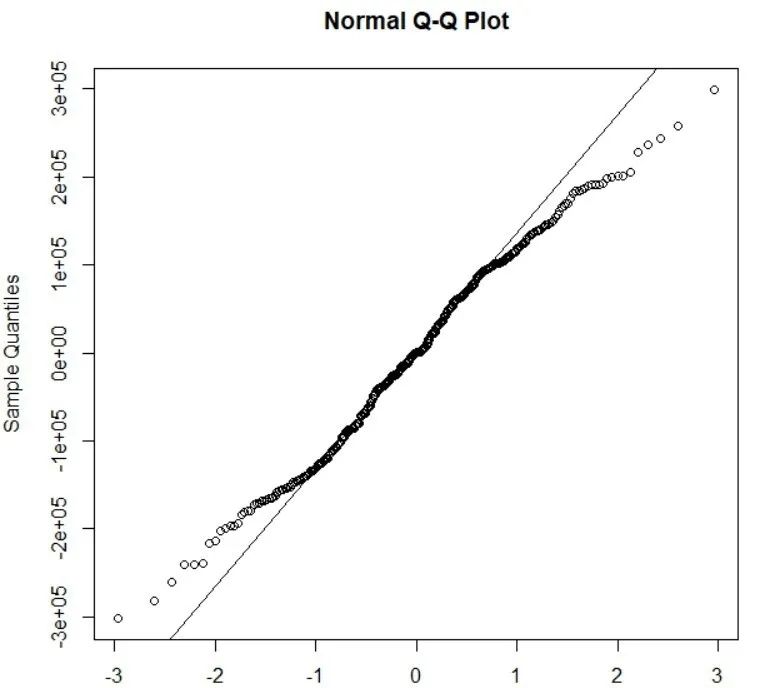
方法二：通过R语言的“Box.test”函数实现该检验，若P>0.05，接受原假设，即任何滞后阶数的残差都不相关，残差检验通过。

03

示例分享

回到开头的例子，当小毛同学拿到数据后首先应该绘制销售额随时间变化的曲线，观察数据的整体趋势，如果有季节性趋势，应该利用差分或者移动平均的方法消除季节因素，接下来在消除增长趋势，然后利用单位根检验来检验数据的平稳性，最后利用数据的ACF和PACF函数确定阶数和模型。

其实在这一步有一种偷懒的办法就是利用R语言中的auto.arima”函数可自动筛选出p，q，但还是希望大家能够了解背后的逻辑。模型确定好之后可以利用R语言中的forecast函数预测未来N期的销量，至此小毛的预测工作终于可以告一段落了。

本次分享到此结束，欢迎大家批评指正~

审核编辑：何安