动态规划：8行代码搞定最大子数组和问题

铁子们，我是小风哥，你也可以叫我岛主

今天给大家带来一道极其经典的题目，叫做最大和子数组，给定一个数组，找到其中的一个连续子数组，其和最大。

示例：

输入:nums=[-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:子数组[4,-1,2,1]的和为6，其它任何连续的子数组和不超过6.

想一想该怎样解决这个问题。

如果你一时想不到解法可以从暴利解法开始。

暴力求解

这种解法最简单，我们把所有子数组找出来，然后依次计算其和，找出一个最大的出来，比如给定数组[1,2,3]，那么我们能找出子数组：[1]，[2]，[3]，[1,2]，[2,3]，[1,2,3]，很显然这里和最大的子数组为[1,2,3]，其值为6。

intsum(vector&nums,intb,inte){
intres=0;
for(;b<= e; b++) {
        res += nums[b];
    }
    returnres;
}
intmaxSubArray(vector&nums){
intsize=nums.size();
intres=0x80000000;
for(inti=0;i< size; i++) {
        for(intj=i;j< size; j++) {
            res = max(res, sum(nums, i, j));
        }
    }
    returnres;
}

这种解法最简单，该算法的时间复杂度为O(n^3)，其中找出所有子数组的时间复杂度为O(n^2)，计算每个子数组的和的时间复杂度为O(n)，因此其时间复杂度为O(n^3)。

让我们再来看一下这个过程，这里的问题在于计算每个子数组的和时有很多重复计算，比如我们知道了子数组[1,2]的和后再计算数组[1,2,3]的值时完全可以利用子数组[1,2]的计算结果而无需从头到尾再算一遍，也就是说我们可以利用上一步的计算结果，这本身就是动态规划的思想。

基于该思想我们可以对上述代码简单改造一下：

intmaxSubArray(vector&nums){
intsize=nums.size();
intres=0x80000000;
for(inti=0;i< size; i++) {
        int sumer = nums[i];
        res = max(res, sumer);
        for(intj=i+1;j< size; j++) {
            sumer += nums[j];
            res = max(res, sumer);
        }
    }
    returnres;
}

看到了吧，代码不但更简洁，而且运行速度更快，该算法的时间复杂度为O(n^2)，比第一种解法高了很多。

还有没有进一步提高的空间呢？

答案是肯定的。

分而治之

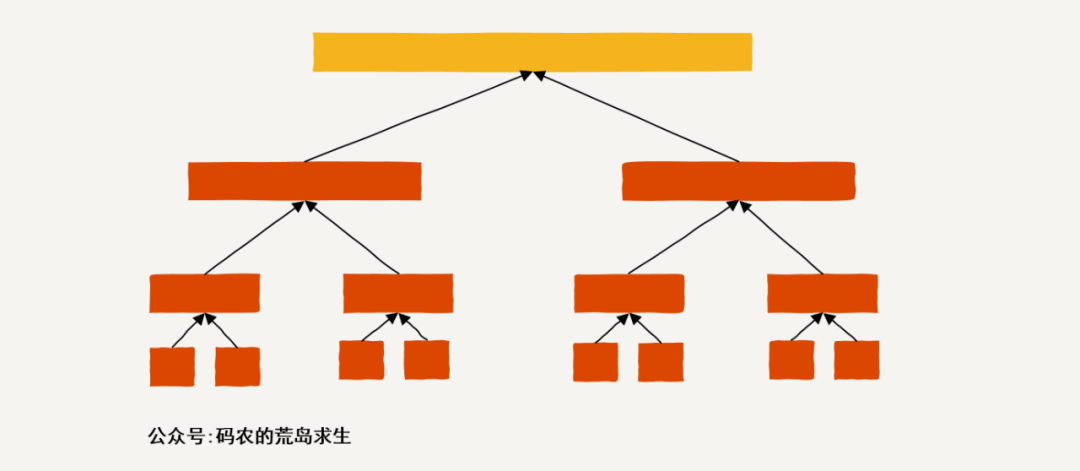
我们在之前的文章中说过，分治也是一种非常强大的思想，具体应该这里的话我们可以把整个数组一分为二，然后子数组也一分为二，不断划分下去就像这样：

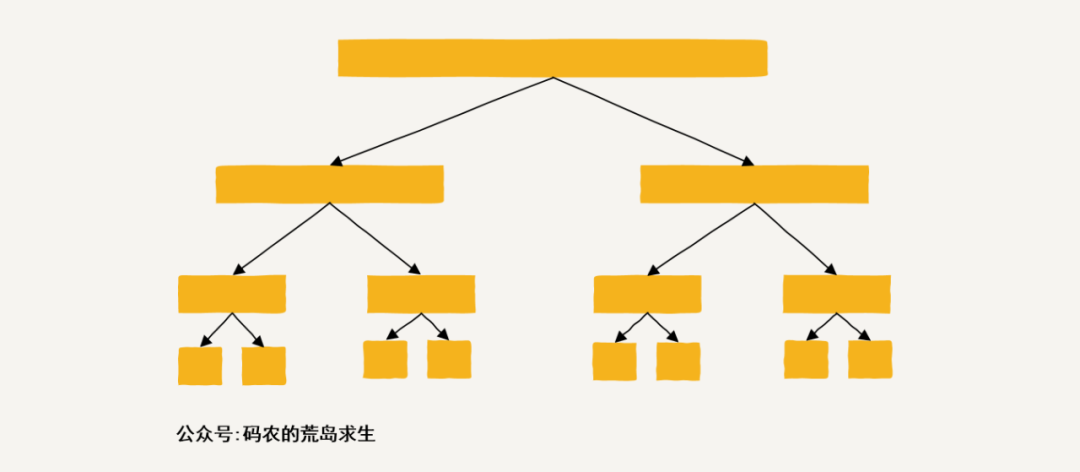
然后呢？

然后问题才真正开始有趣起来，注意，当我们划分到最下层的时候，也就是不可再划分时会得到两个数组元素，比如对于数组[1,2]会划分出[1]与[2]，此时[1]与[2]不可再划分，那么对于子问题[1,2]，其最大子数组的和为max(1+2, 1,2)，也就是说要么是左半部分的元素值、要么是右半部分的元素值、要么是两个元素的和，就这样我们得到了最后两层的答案：

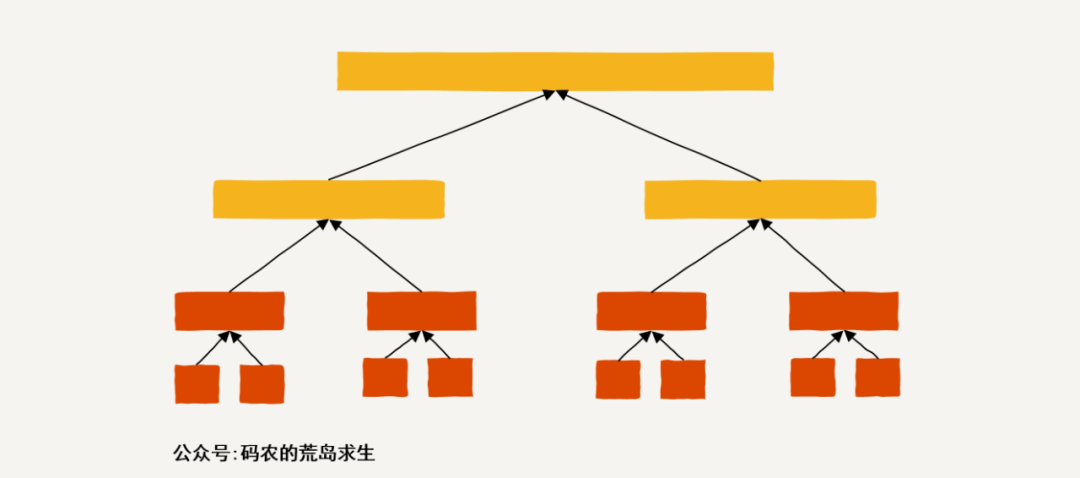
假设对于数组[1,2,3,4]，一次划分后得到了[1,2]与[3,4]，用上面的方法我们可以分别知道这两个问题的最大子数组和，我们怎样利用上述的答案来解决更大的问题，也就是[1,2,3,4]呢？

很显然，对于[1,2,3,4]来说，最大子数组的和要么来自左半部分、要么来自右半部分、要么来自中间部分——也就是包含2和3，其中左半部分和右半部分的答案我们有了，那么中间部分的最大和该是多少呢？

其实这个问题很简单，我们从中间开始往两边不断累加，然后记下这个过程的最大值，比如对于[1,-2,3,-4,5]，我们从中间的3开始先往左边累加和是:{1+(-2)+3, (-2)+3, 3}也就是{2,1,3}，因此我们以中间数字为结尾的最大子数组和为3：

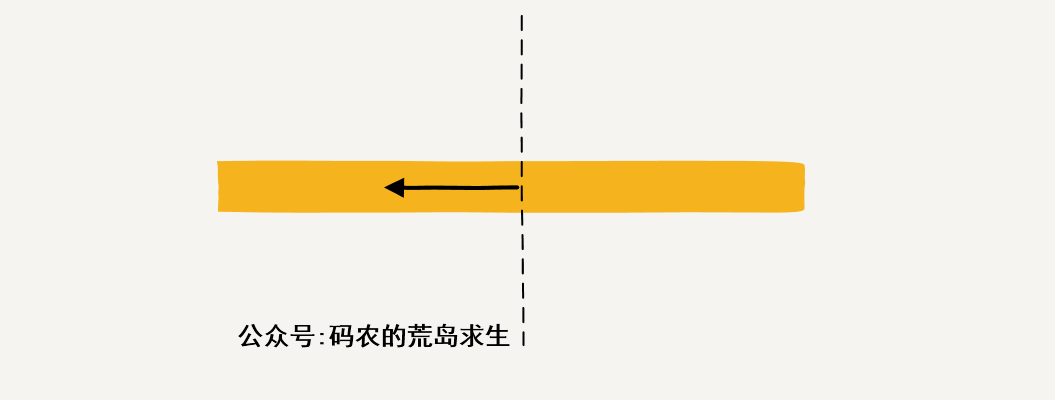
另一边也是同样的道理，只不过这次是以中间数字为起点向右累加：

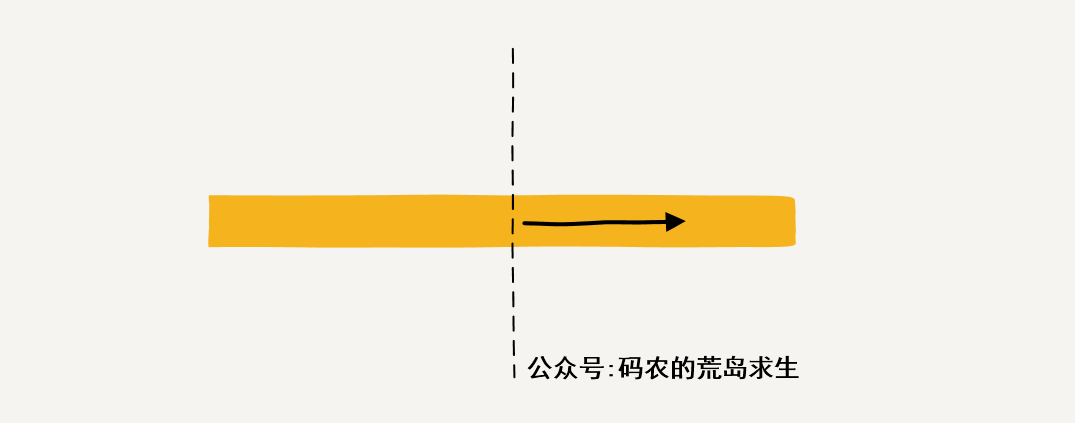
然后这三种情况中取一个最大值即可，这样我们就基于子问题解决了更大的问题：

此后的道理一样，最终我们得到了整个问题的解。

根据上面的分析就可以写代码了：

intgetMaxSum(vector&nums,intb,inte){
if(b==e)returnnums[b];
if(b==e-1)returnmax(nums[b],max(nums[e],nums[b]+nums[e]));
intm=(b+e)/2;
intmaxleft=nums[m];
intmaxright=nums[m];
intsum=nums[m];

for(inti=m+1;i<= e; i++) {
        sum += nums[i];
        maxright = max(maxright, sum);
    }

    sum = nums[m];
    for(inti=m-1;i>=b;i--){
sum+=nums[i];
maxleft=max(maxleft,sum);
}
returnmax(getMaxSum(nums,b,m-1),max(getMaxSum(nums,m+1,e),maxleft+maxright-nums[m]));
}
intmaxSubArray(vector&nums){
returngetMaxSum(nums,0,nums.size()-1);
}

上述这段代码的时间复杂度为O(NlogN)比第二种方法又提高了很多。

动态规划

实际上这个问题还有另一种更妙的解决方法，我们令dp(i)表示以元素A[i]为结尾的最大子数组的和，那么根据这一定义则有：

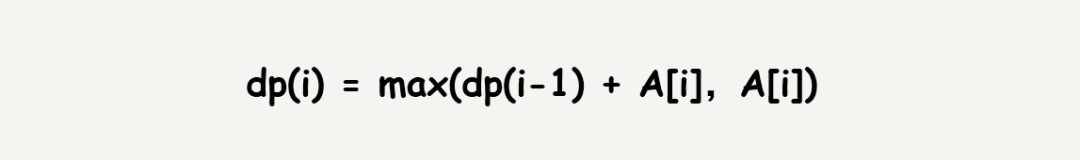
这是很显然的，注意dp(i)的定义，是以元素A[i]为结尾的最大子数组的和，因此dp(i)的值要么就是A[i]连接上之前的一个子数组，那么不链接任何数组，那么最终的结果一定是以某个元素为结尾的子数组，因此我们从所有的dp(i)中取一个最大的就好了，依赖子问题解决当前问题的解就是所谓的动态规划。

有了这些分析，代码非常简单：

intmaxSubArray(vector&nums){
intsize=nums.size();
vectordp(size,0);
intres=dp[0]=nums[0];
for(inti=1;i< size; i++) {
        dp[i] = max(dp[i - 1] + nums[i], nums[i]);
        res = max(res, dp[i]);
    }
    returnres;
}

这段代码简单到让人难以置信，只有8行代码，你甚至可能会怀疑这段代码的正确性，但它的确是没有任何问题的，而且这段代码的时间复杂度只有O(N)，这段代码既简单运行速度又快，这大概就是算法的魅力吧。

审核编辑 ：李倩