怎么理解谐波分析(FFT)?本文将通过常用例子介绍傅立叶变化,以及计算过程中遇到幅值泄漏和栅栏效应,加窗函数原则和最后修复幅值、频率的基本原理,并给出其在高端测量仪器中的应用。
随着技术的发展,数据越来越多样化,不再以单一的形式存在,例如一段录音可被分解成若干种信息,而快速傅立叶变化(简称FFT)常常被应用在数据的分解上,接下来我们讲讲FFT的原理。
什么是FFT?
快速傅立叶变化简称FFT,其实FFT就是DFT(离散傅立叶变化)的一种快速算法,通过时间抽取或频率抽取算法来加快变化过程,具体的算法就不在这里拓展,我们只要了解离散傅立叶变化即可。举个简单的例子,假如手机里正在播放一首音乐,随着时间的推移,歌曲是不是按照它的音符播放呢?若以高低音作为纵轴,时间左右横轴建立直角坐标得到(图1-1),以音符作为横轴建立直角坐标得到(图1-2)。
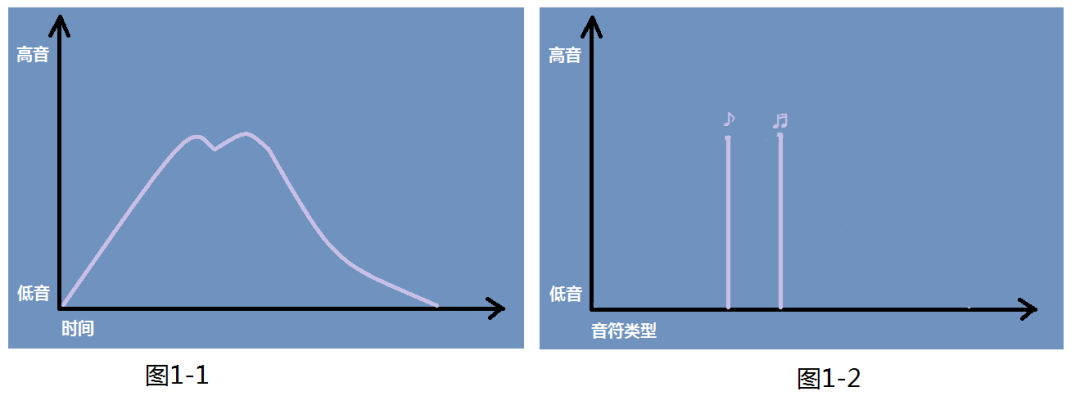
图1生活中FFT例子
我们称图1中图1-1为时域,图1-2称为频域,数据由时域转换为频域的过程我们称为傅立叶转换(图2),由于转换后的频域数据是不连续的,所以为离散傅立叶转换。其中转换后得到的频谱图中频率不为零且幅值最大的一般都是基波,也叫零次谐波。
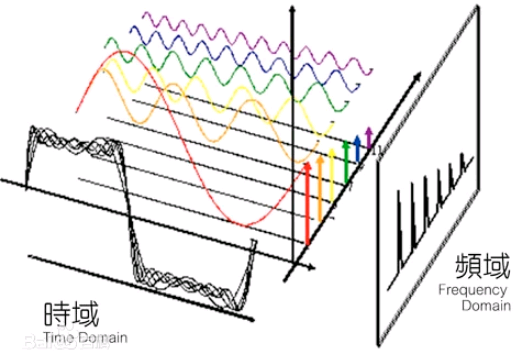

图2 时域到频域
什么是频率泄漏?
谐波分析一段采集时间较长的数据,需要将数据切成一帧帧进行分析,这个过程称为信号截断。信号截断分为周期截断和非周期截断。这一点还是比较好理解,就是在数据切成一帧帧的时候,每帧数据是否为周期信号进而判断是哪种类型截断。如图3显示。
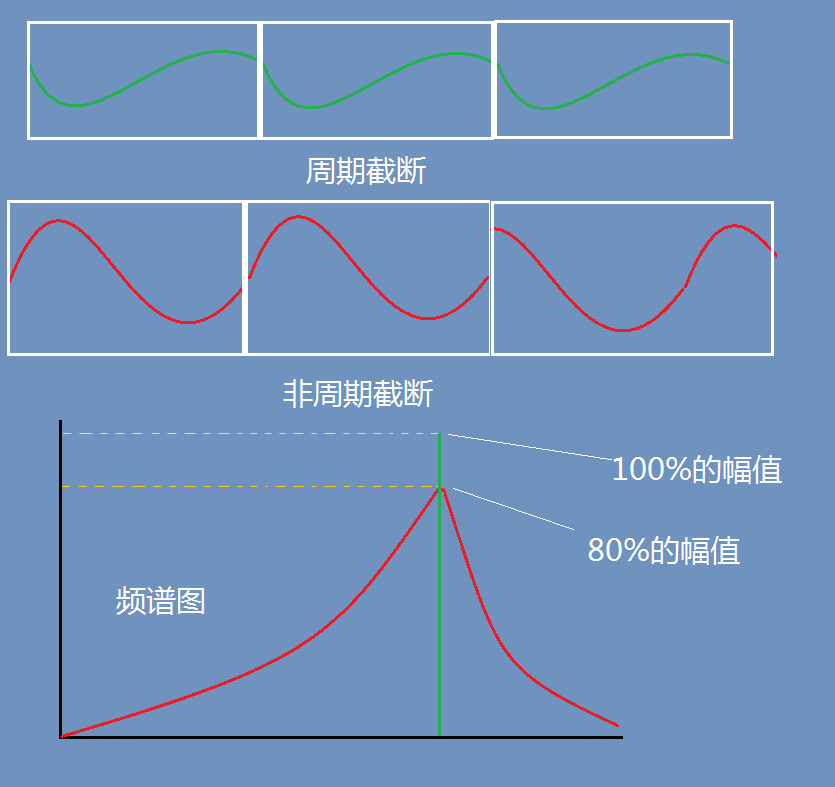
图3信号截断
周期截断不存在谐波泄漏,这是因为信号频率成分为频率分辨率的整数倍。非周期截断如图所示,由于重新组成数据进行谐波分析幅值出现拖尾,即会造成如图3-2频谱图的现象,所以信号的非周期截断,导致频谱在整个频带内发生了拖尾现象,由于能力守恒最终导致幅值比原来的低,这就是幅值泄漏。
栅栏效应
栅栏效应指的是离散傅立叶变化过程的频谱被限制在基频整数倍处,犹如栅栏一样关注的频率主要分布在木块之间,如图4所示。
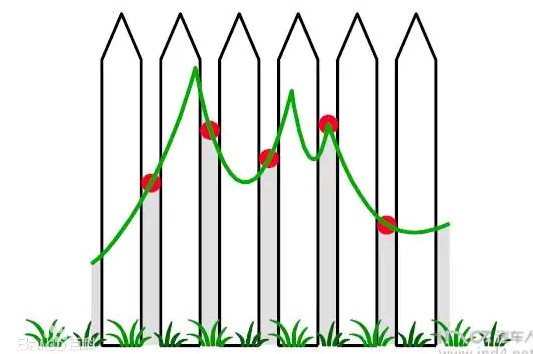
图4栅栏效应
窗函数及类型
前面已经了解泄漏问题,我们可以通过加合适的窗函数来尽可能减少频谱拖尾的现象,那么什么是窗函数呢?简单理解就是不同的信号截断函数如图5所示,常见的窗函数有以下几种:
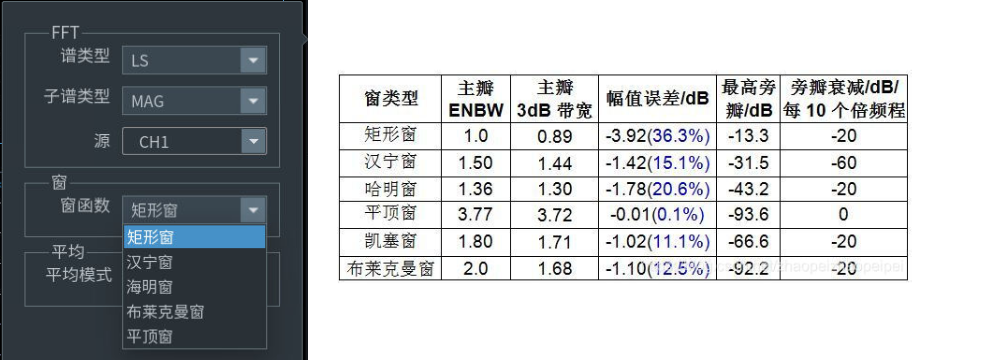
图5 窗函数类型
矩形窗相当为没加窗,常用于周期信号;信号随机或未知,或者多个频率分量,测试关注是频率而非能量大小,则选择汉宁窗;对校准目的,要求幅值精准,适用平顶窗;如果要求幅值频率的精度,则选择凯塞窗;检测两信号频率相近,幅值不同的,建议用布莱克曼窗。  加窗后幅值和频率修正
加窗后幅值和频率修正
通过前面已经了解加窗函数可减少泄漏现象,但频率栅栏效应没得到修复,加窗后幅值泄漏现象也只得到缓解,那么可以通过插值算法来得到一个准确的幅值和频率。算法原理是各个频率成分主瓣形状将近似窗函数频谱的主瓣形状,如果这形状可以用某个函数来描述,则可利用主峰两侧的谱线通过插值计算出主峰的高度,从而克服栅栏效应。具体的推导可查看《Hanning窗在插值FFT算法中应用的研究》这一文献。
支持谐波分析的高端仪器
示波记录仪ZDL6000支持波形离线和在线的谐波分析,离线最高可支持10M一帧进行FFT分析,支持多种窗函数设置,支持多个通道同时计算且支持回读数据进行分析,如图7。
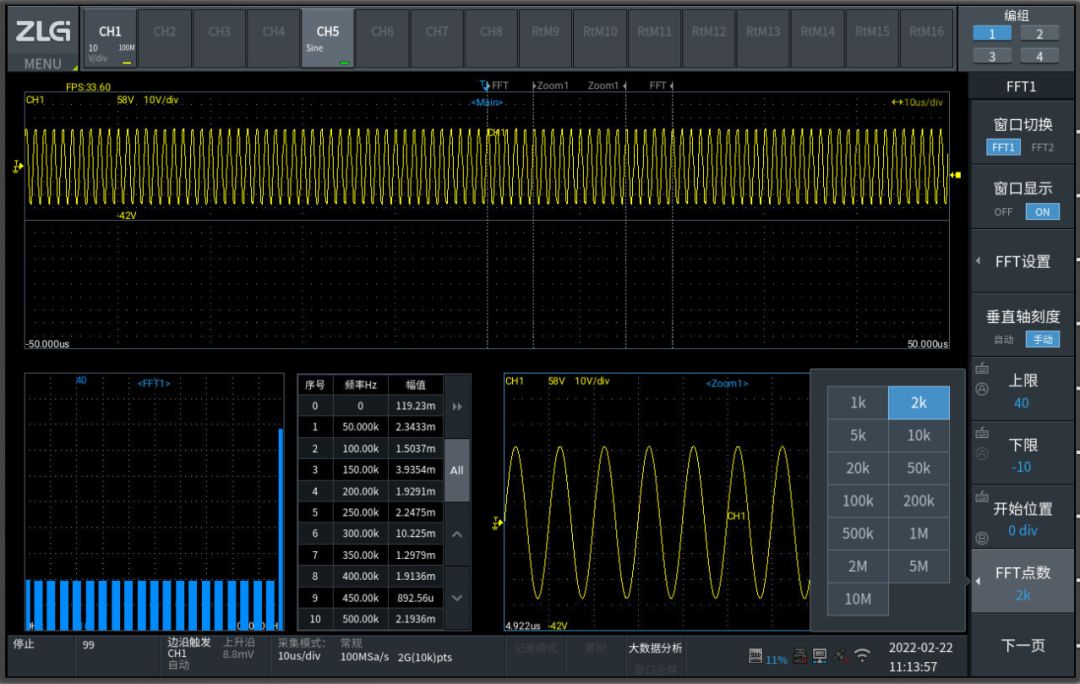
图7离线FFT分析
在线支持最高采样率2M,多个通道同步采集计算分析,每帧数据分析周期可设置1~100ms,支持分析15次谐波,并自动刷新保存导出csv文件。如图8所示。
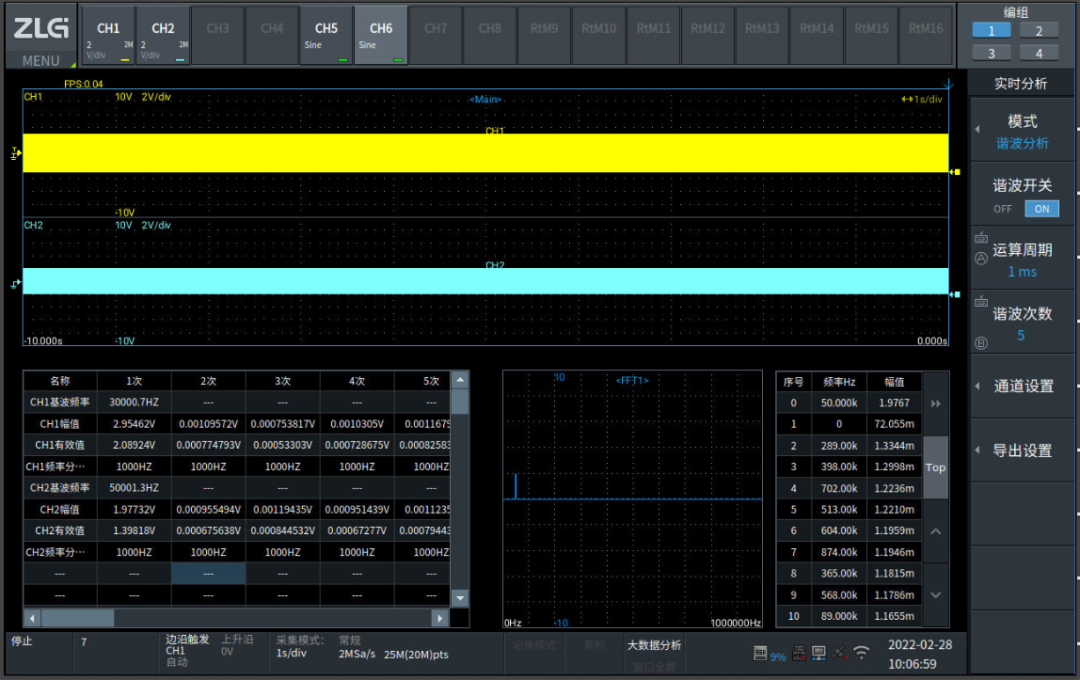
图8在线FFT分析
得到的谐波分析结果支持二次运算,可自动导出csv等强大功能。
审核编辑 :李倩
-
算法
+关注
关注
23文章
4642浏览量
93664 -
FFT
+关注
关注
15文章
438浏览量
59781 -
傅立叶
+关注
关注
0文章
36浏览量
12602
原文标题:一看就懂:FFT算法讲解及应用
文章出处:【微信号:ZLG_zhiyuan,微信公众号:ZLG致远电子】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
Dac5687测试发现谐波分量很大,为什么?
如何进行谐波检测
如何通过驻波分析电路
ADC量化位数只有两位,将采样结果做FFT分析后,发现二次谐波的幅度最大,请教是什么原因造成的?
利用ADS127L01采样10kHz信号,采样数据上位机fft变换得到部分谐波分量输出较大,怎么解决?
PZ系列可编程智能电测仪表——谐波功能安装使用说明书 V1.3
浅谈医院配电系统谐波分析及治理方案
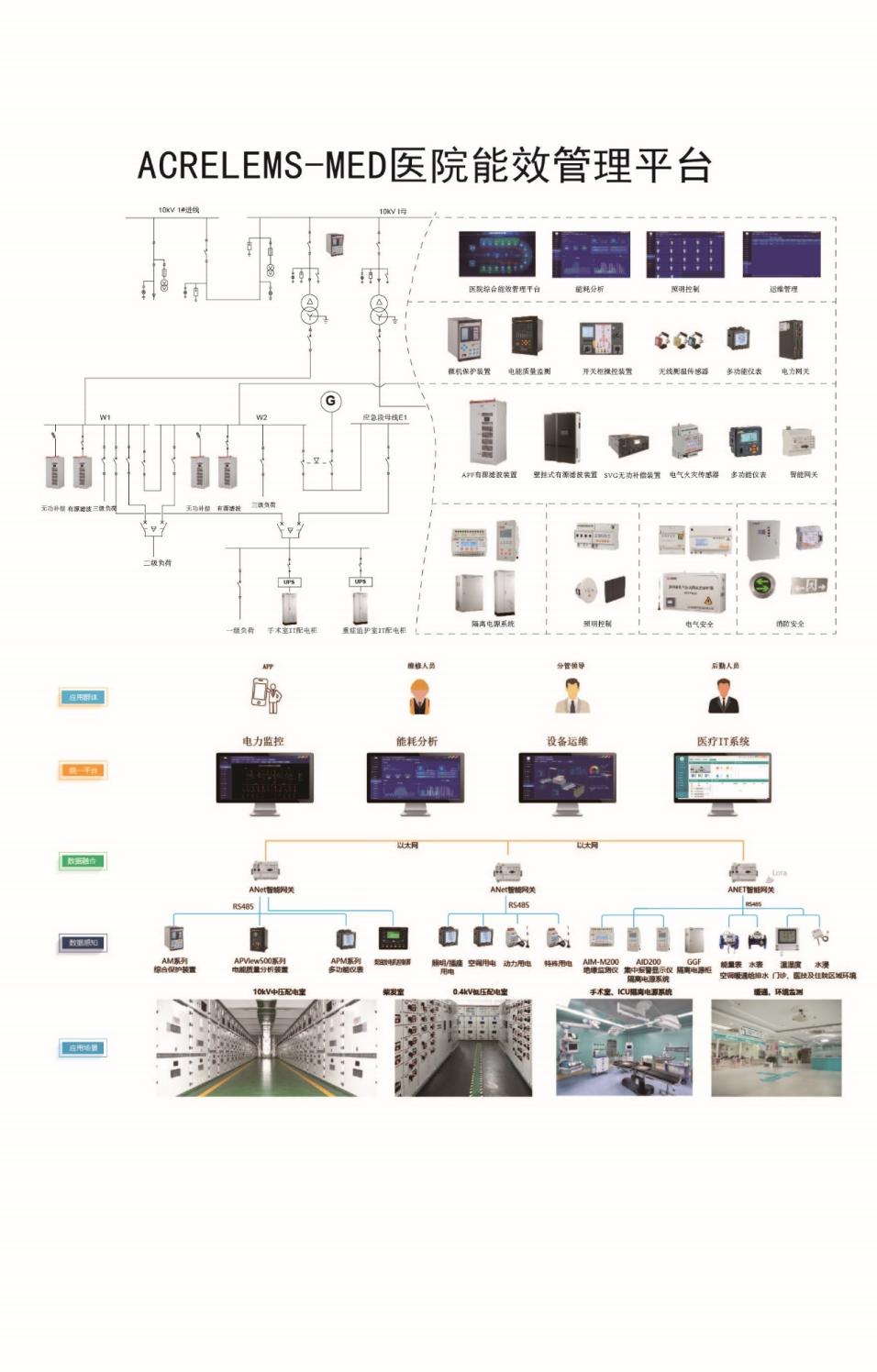
关于医院配电系统谐波分析与治理技术解决方案
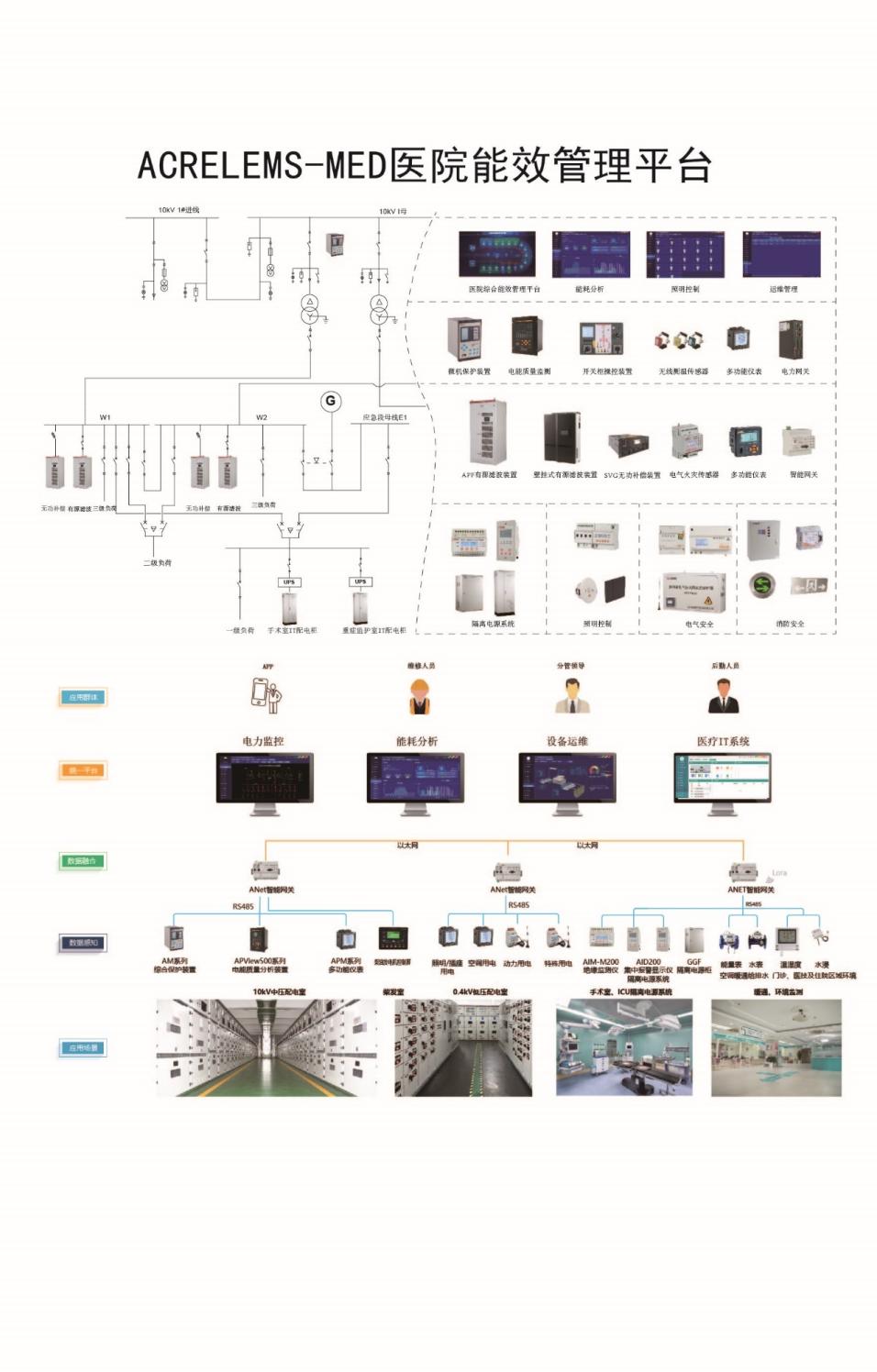
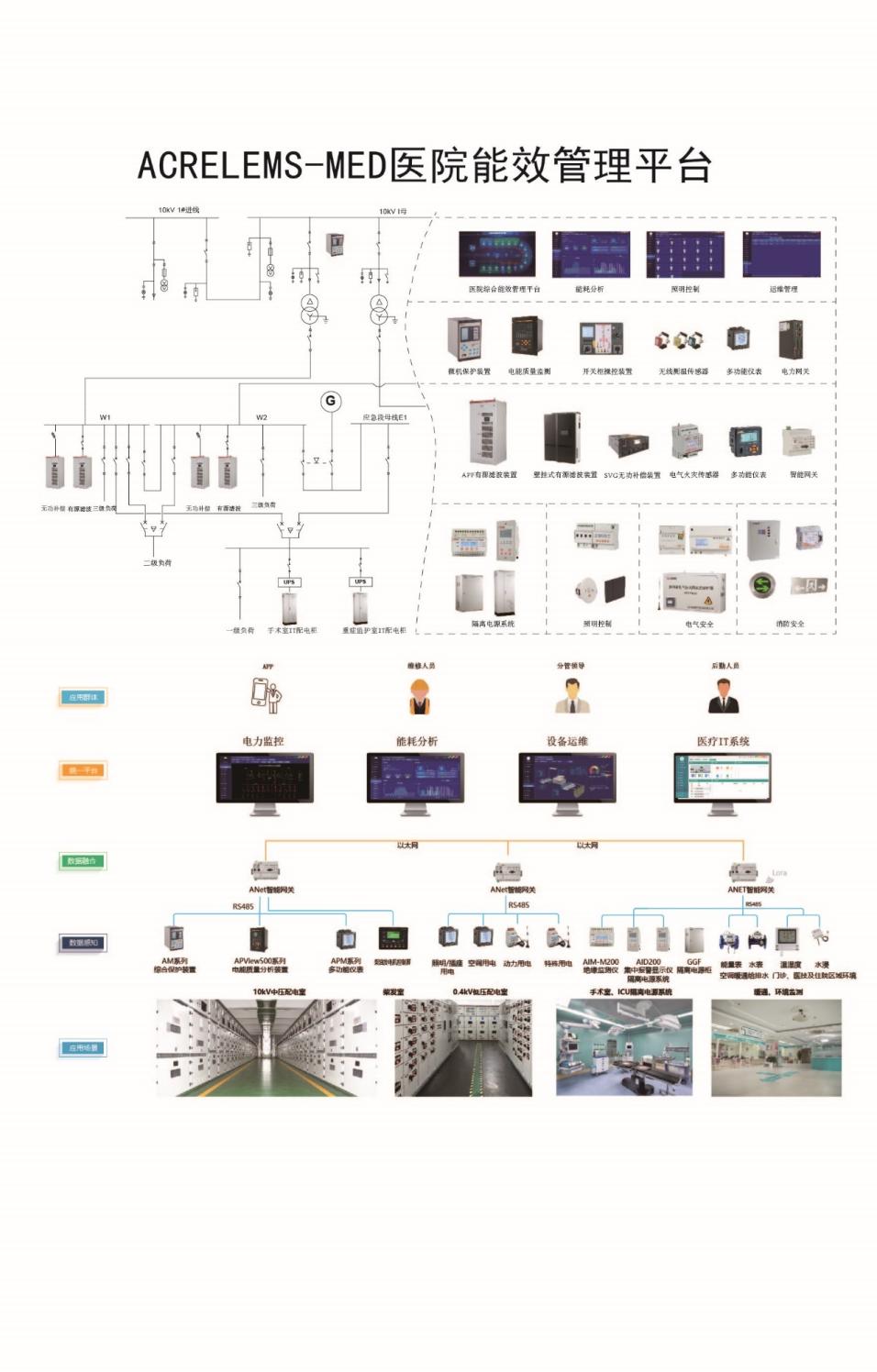
浅谈医院配电系统谐波分析与治理技术方案
电动机经济运行分析仪MEDJY-M操作说明——每日了解电力知识

安科瑞APview500电能质量监测装置 谐波分析电压闪变监测

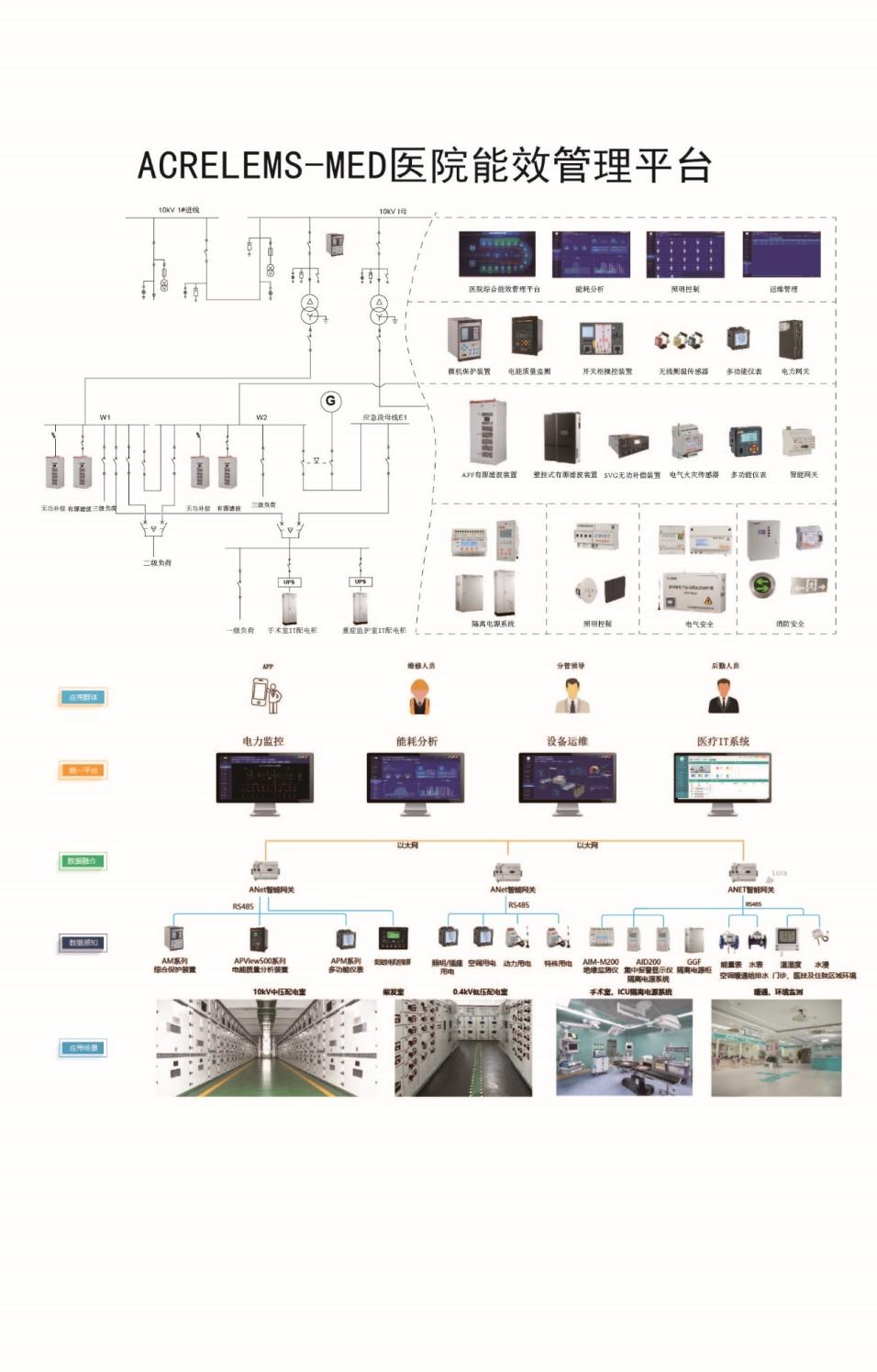
浅谈医院配电系统谐波分析及治理研究
基波是一次谐波么 基波与一次谐波的区别
示波器的 FFT 功能怎么调?
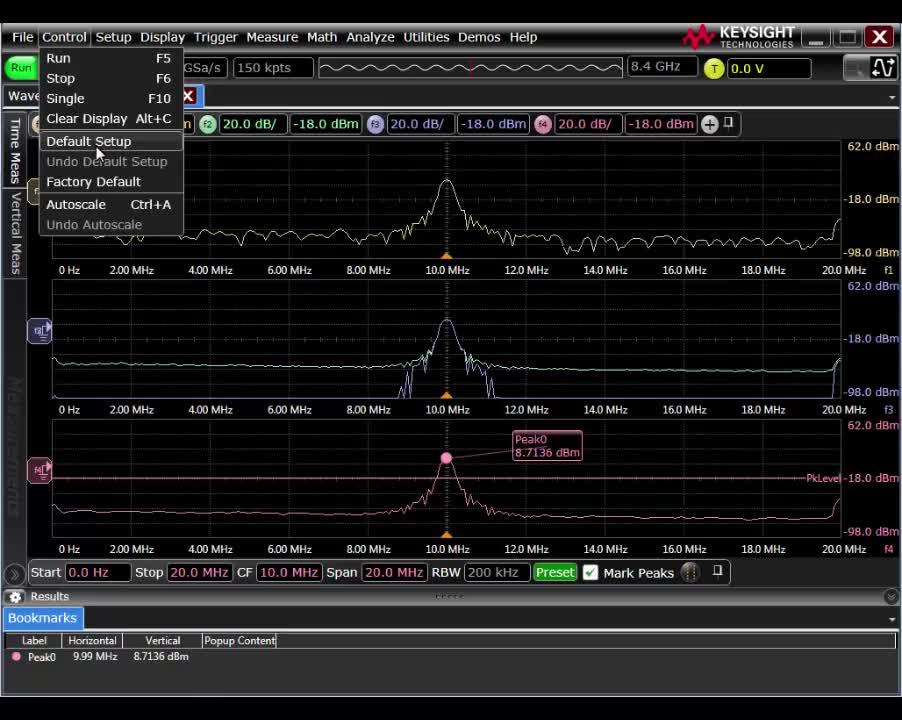




 怎么理解谐波分析(FFT)?
怎么理解谐波分析(FFT)?










评论