如何使用RAPIDS和CuPy时加速Gauss 秩变换

正如在 批量标准化纸 中所解释的，如果神经网络的输入是高斯的，那么训练它就变得容易多了。这很清楚。如果你的模型输入不是高斯的， RAPIDS 会在眨眼间把它转换成高斯的。

高斯秩变换 是一种新的标准化技术，用于转换输入数据以训练深层神经网络。最近，我们在 预测分子竞争性质 中使用了这种技术，它很容易将 m 消息传递神经网络模型 的精度提高了一个显著的幅度。这篇博文将展示如何使用 RAPIDS cuDF 和 Chainer CuPy 实现 GPU 加速的Gauss 秩变换，并使用 pandas 和 NumPy 替换来实现 100 倍加速 。

介绍

输入归一化是训练神经网络的关键。高斯秩变换的思想最早是由 迈克尔·贾勒。 在他的 塞古罗港的安全驾驶预测 挑战的胜利解中提出的。他训练去噪自动编码器，并尝试了几种输入标准化方法。最后，他得出这样的结论：

我在过去发现的最棒的东西是 GaussRank ，它能直接发挥作用。这通常比标准的 mean / std 定标器或 min / max （标准化）好得多。

工作原理

有三个步骤可以将任意分布下的连续值向量转换为基于秩的高斯分布，如图 1 所示。

图 1 ：高斯秩变换。

CuPy 实现非常简单，非常类似于 NumPy 操作。实际上，只需更改导入的函数，就可以将整个进程从 CPU 移动到 GPU ，而无需任何其他代码更改。

import cupy as cp
from cupyx.scipy.special import erfinv
import matplotlib.pyplot as plt
import numpy as np
from scipy.special import erfinv as sp_erfinv

x_gpu = cp.random.rand(20) # input array
x_cpu = cp.asnumpy(x_gpu)
x_gpu

Out[1]:

array([0.55524998, 0.42394212, 0.01200076, 0.13974612, 0.74289723,
       0.19072088, 0.47061846, 0.61921186, 0.96994115, 0.44076614,
       0.04326316, 0.33698309, 0.47978816, 0.00819107, 0.63463167,
       0.03370001, 0.0369827 , 0.84651929, 0.25335235, 0.75172228])

In[2]:

r_gpu = x_gpu.argsort().argsort() # compute the rank
print(r_gpu)

r_cpu = x_cpu.argsort().argsort() 
print(r_cpu)

[13  9  1  5 16  6 11 14 19 10  4  8 12  0 15  2  3 18  7 17]
[13  9  1  5 16  6 11 14 19 10  4  8 12  0 15  2  3 18  7 17]

In[3]:

r_gpu = (r_gpu/r_gpu.max()-0.5)*2 # scale to (-1,1)
epsilon = 1e-6
r_gpu = cp.clip(r_gpu,-1+epsilon,1-epsilon)
print(r_gpu)

r_cpu = (r_cpu/r_cpu.max()-0.5)*2 # scale to (-1,1)
r_cpu = cp.clip(r_cpu,-1+epsilon,1-epsilon)
print(r_cpu)

[ 0.36842105 -0.05263158 -0.89473684 -0.47368421  0.68421053 -0.36842105
  0.15789474  0.47368421  0.999999    0.05263158 -0.57894737 -0.15789474
  0.26315789 -0.999999    0.57894737 -0.78947368 -0.68421053  0.89473684
 -0.26315789  0.78947368]
[ 0.36842105 -0.05263158 -0.89473684 -0.47368421  0.68421053 -0.36842105
  0.15789474  0.47368421  0.999999    0.05263158 -0.57894737 -0.15789474
  0.26315789 -0.999999    0.57894737 -0.78947368 -0.68421053  0.89473684
 -0.26315789  0.78947368]

In[4]:

r_gpu = erfinv(r_gpu) # map to gaussian
print(r_gpu)

r_cpu = sp_erfinv(r_cpu) # map to gaussian
print(r_cpu)

[ 0.3390617  -0.0466774  -1.14541135 -0.44805114  0.70933273 -0.3390617
  0.14085661  0.44805114  3.45891074  0.0466774  -0.56893556 -0.14085661
  0.23761485 -3.45891074  0.56893556 -0.8853822  -0.70933273  1.14541135
 -0.23761485  0.8853822 ]
[ 0.3390617  -0.0466774  -1.14541135 -0.44805114  0.70933273 -0.3390617
  0.14085661  0.44805114  3.45891074  0.0466774  -0.56893556 -0.14085661
  0.23761485 -3.45891074  0.56893556 -0.8853822  -0.70933273  1.14541135
 -0.23761485  0.8853822 ]

In[5]:

n_bins = 5
fig, axs = plt.subplots(1, 2, sharey=True, tight_layout=True)
fig.set_figheight(5)
fig.set_figwidth(15)
axs[0].hist(cp.asnumpy(x_gpu), bins=n_bins)
axs[0].set_title('input',fontsize=15)
axs[1].hist(cp.asnumpy(r_gpu), bins=n_bins)
axs[1].set_title('transform',fontsize=15)
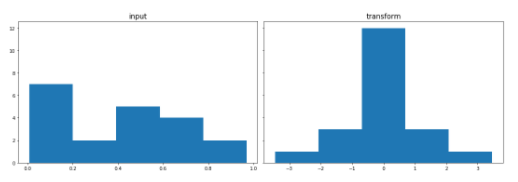
print('GaussRank transformation GPU')

GaussRank transformation

In[6]:

n_bins = 5
fig, axs = plt.subplots(1, 2, sharey=True, tight_layout=True)
fig.set_figheight(5)
fig.set_figwidth(15)
axs[0].hist(x_cpu, bins=n_bins)
axs[0].set_title('input',fontsize=15)
axs[1].hist(r_cpu, bins=n_bins)
axs[1].set_title('transform',fontsize=15)
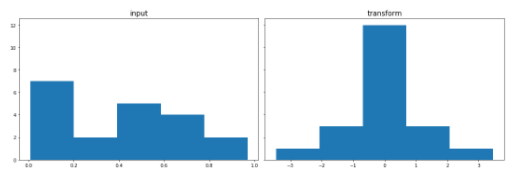
print('GaussRank transformation CPU')

GaussRank transformation CPU

反变换用于从高斯变换中恢复原始值。这是展示 cuDF 与 CuPy 的互操作性 的另一个很好的例子。就像您可以使用 NumPy 和 pandas 一样，您可以在同一个工作流中将 cuDF 和 CuPy 编织在一起，同时将数据完全保存在 GPU 上。

import warnings
warnings.filterwarnings("ignore")

import cupy as cp
from cupyx.scipy.special import erfinv
import cudf as gd

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.special import erfinv as sp_erfinv

GaussRank transformation

In[2]:

x_gpu = cp.random.rand(20) # input array
x_cpu = cp.asnumpy(x_gpu)

r_gpu = x_gpu.argsort().argsort() # compute the rank
r_cpu = x_cpu.argsort().argsort() 

r_gpu = (r_gpu/r_gpu.max()-0.5)*2 # scale to (-1,1)
epsilon = 1e-6
r_gpu = cp.clip(r_gpu,-1+epsilon,1-epsilon)

r_cpu = (r_cpu/r_cpu.max()-0.5)*2 # scale to (-1,1)
r_cpu = cp.clip(r_cpu,-1+epsilon,1-epsilon)

r_gpu = erfinv(r_gpu) # map to gaussian
r_cpu = sp_erfinv(r_cpu) # map to gaussian

Inverse transformation step by step

In[3]:

df_cpu = pd.DataFrame({'src':x_cpu,'tgt':r_cpu}) 
df_gpu = gd.DataFrame({'src':x_gpu,'tgt':r_gpu}) # pass cupy array to cudf dataframe

df_cpu = df_cpu.sort_values('src') # sort
df_gpu = df_gpu.sort_values('src')

pos_cpu = df_cpu['tgt'].searchsorted(r_cpu, side='left') # search
pos_gpu = df_gpu['tgt'].searchsorted(r_gpu, side='left')

In[4]:

def linear_inter_polate(df,x,pos):
    N = df.shape[0]
    pos[pos>=N] = N-1
    pos[pos-1<=0] = 0
    if isinstance(x,cp.ndarray):
        pos = pos.values
        
    x1 = df['tgt'].values[pos]
    x2 = df['tgt'].values[pos-1]
    y1 = df['src'].values[pos]
    y2 = df['src'].values[pos-1]

    relative = (x-x2)  / (x1-x2)
    return (1-relative)*y2 + relative*y1

In[5]:

x_inv_cpu = linear_inter_polate(df_cpu,r_cpu,pos_cpu) # linear inter polate
x_inv_gpu = linear_inter_polate(df_gpu,r_gpu,pos_gpu)

In[6]:

n_bins = 5
fig, axs = plt.subplots(1, 3, sharey=True, tight_layout=True)
fig.set_figheight(5)
fig.set_figwidth(15)
axs[0].hist(x_cpu, bins=n_bins)
axs[0].set_title('input',fontsize=15)
axs[1].hist(r_cpu, bins=n_bins)
axs[1].set_title('transform',fontsize=15)
_ = axs[2].hist(x_inv_cpu, bins=n_bins)
axs[2].set_title('inverse transform',fontsize=15)
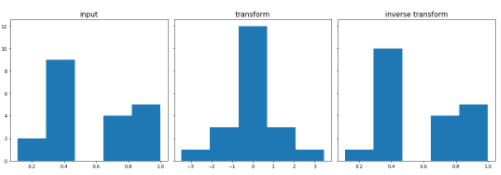
print('GaussRank CPU')

GaussRank CPU

In[7]:

n_bins = 5
fig, axs = plt.subplots(1, 3, sharey=True, tight_layout=True)
fig.set_figheight(5)
fig.set_figwidth(15)
axs[0].hist(cp.asnumpy(x_gpu), bins=n_bins)
axs[0].set_title('input',fontsize=15)
axs[1].hist(cp.asnumpy(r_gpu), bins=n_bins)
axs[1].set_title('transform',fontsize=15)
_ = axs[2].hist(cp.asnumpy(x_inv_gpu), bins=n_bins)
axs[2].set_title('inverse transform',fontsize=15)
print('GaussRank GPU')

GaussRank GPU

一个真实的例子

对于本例，我们将使用 CHAMPS 分子性质预测数据集 。这项任务是预测八种不同化学键类型的分子中原子对之间的 标量耦合常数 （基本真理） 。具有挑战性的是，对于每种键类型，基本真值的分布都有很大的不同，均值和方差也不同。这使得神经网络很难收敛。

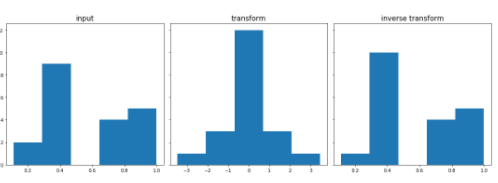
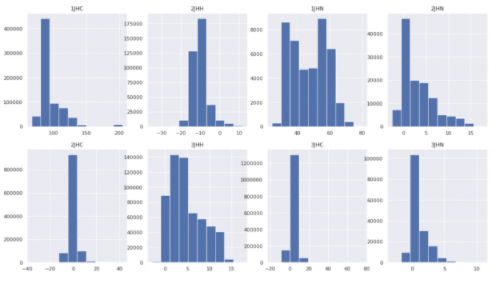
图 2 ：每种键合类型的基本事实分布。

因此，我们将高斯秩变换应用于训练数据的基本事实，为所有键类型创建一个统一的干净高斯分布。

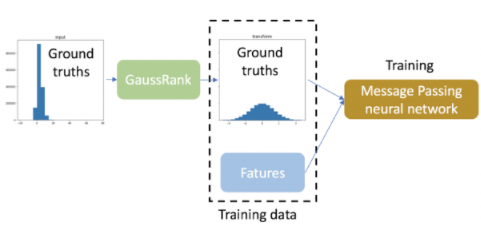
图 3 ：使用 GaussRank 转换基本事实的工作流程。

在这个回归任务中，使用 GaussRank 变换训练数据的基本事实。

为了进行推断，我们将反高斯秩变换应用于测试数据的预测，以便它们匹配每种键类型的原始不同分布。由于测试数据中目标的真实分布是未知的，因此根据训练数据中目标变量的分布计算测试数据预测的逆变换。应该注意的是，这种逆变换只需要用于目标变量。

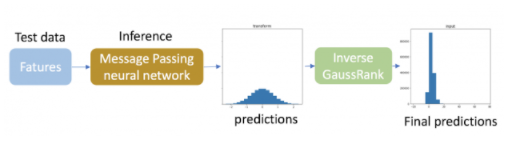
图 4 ：预测被反变换以匹配原始分布。

通过运用这一技巧 平均绝对误差（ LMAE ）的对数 of our message passing neural network is improved by 18%！

请记住 GaussRank 确实有一些限制：

它只适用于连续变量，并且

如果输入已经接近高斯分布，或者非常不对称，则性能 MIG ht 不会得到改善，甚至变得更差。

高斯秩变换与各种神经网络的相互作用是一个非常活跃的研究课题。

加速

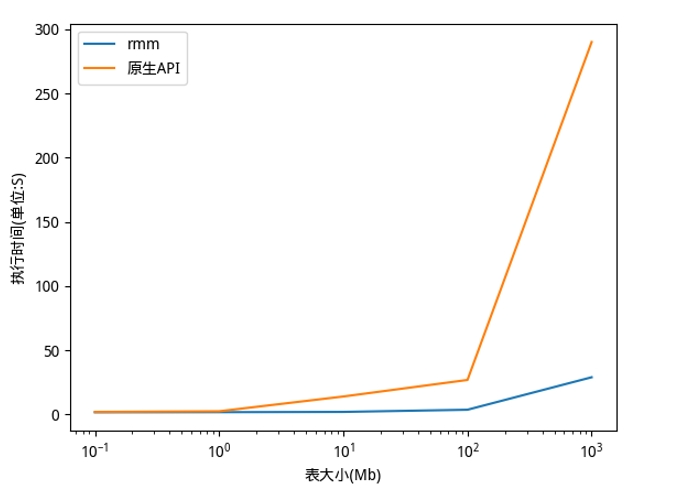
我们测量变换和反变换的总时间。对于正在进行的 CHAMPS 数据集， cuDF + CuPy 在单个 NVIDIA V100 GPU 上的实现在 Intel Xeon CPU 上实现了 比 pandas + NumPy 快 25 倍 。我们生成 合成随机数据 以进行更全面的比较。对于 10M 及以上的数据点，我们的 RAPIDS 实现比 快 100 倍。 多

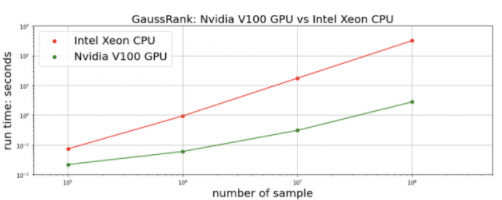
图 5 ： GaussRank 变换+反变换对合成随机数据的加速比较。

结论

RAPIDS 在提供惊人的性能方面取得了长足的进步，代码几乎没有变化。这篇博文展示了使用 RAPIDS cuDF 和 CuPy 作为 pandas 和 NumPy 的替代品来实现 gpu 性能改进是多么容易。如中所示 完整的笔记本 ，通过 只添加两行代码 ，高斯秩变换检测到输入张量在 GPU 上，并自动从 pandas + NumPy 切换到 cuDF + CuPy 。再简单不过了。

关于作者

Jiwei Liu 是 NVIDIA 的数据科学家，致力于 NVIDIA 人工智能基础设施，包括 RAPIDS 数据科学框架。

审核编辑：郭婷