峰值电流模式降压转换器反馈补偿的设计过程

峰值电流模式控制的降压转换器目前在消费电子产品和计算机外围电源管理中非常流行和广泛采用。本应用笔记介绍了峰值电流模式降压转换器反馈补偿的设计过程，还介绍了用于电路仿真的 SIMPLIS 工具和用于定量设计的 Mathcad 数学软件，最后通过实际测量提供了验证结果。

1. 峰值电流模式降压转换器的开环分析

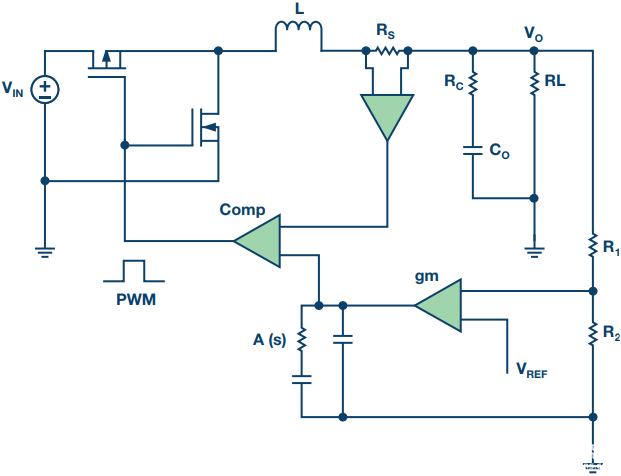
峰值电流模式控制由内部电流环路实现，该环路由电流检测电路 R i和斜率补偿（锯齿形斜坡）电路组成。检测到的电流斜坡与锯齿斜坡相加，然后与误差放大器的输出 V C进行比较。结果用于控制 MOSFET 的导通时间 T ON。电路图如图1所示。

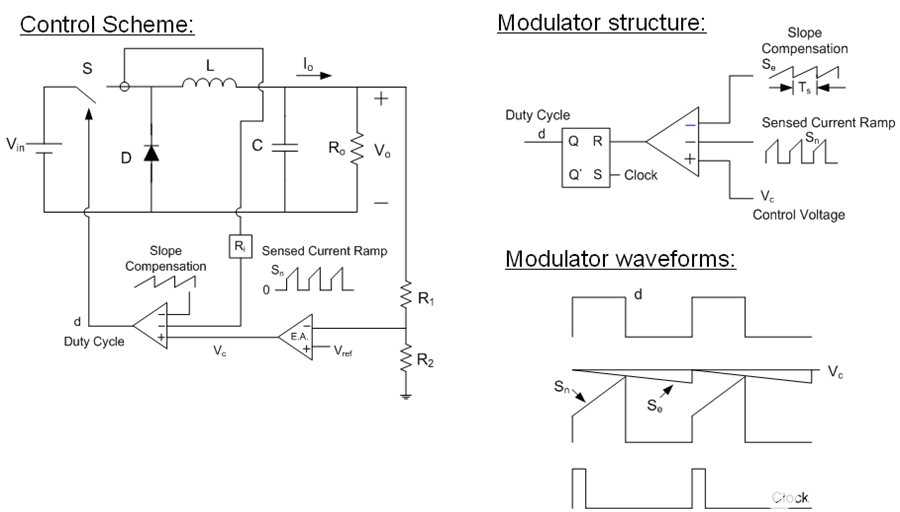
图 1. 峰值电流模式降压转换器的电路图

对于峰值电流模式，当占空比 D 》 0.5 时，可能会出现次谐波振荡。在图 2 中，T ON是 MOSFET 的导通时间，T S 是切换周期；虚线表示受扰动的电感电流，实线表示理想的稳态电感电流。对于 D 《 0.5，如果开始扰动，几个周期后它将完全阻尼；也就是说，由扰动引起的不稳定状态会逐渐稳定下来。但是，对于 D 》 0.5，如果开始扰动，它将在接下来的几个周期中继续增加，从而使系统不稳定。因此引入斜率补偿以消除这种次谐波振荡的风险，从而使系统能够保持稳定。斜率补偿是通过将与控制电路频率相同的锯齿斜坡添加到感测的电感电流斜坡来实现的，这样系统在占空比高于 0.5 时仍然可以稳定。

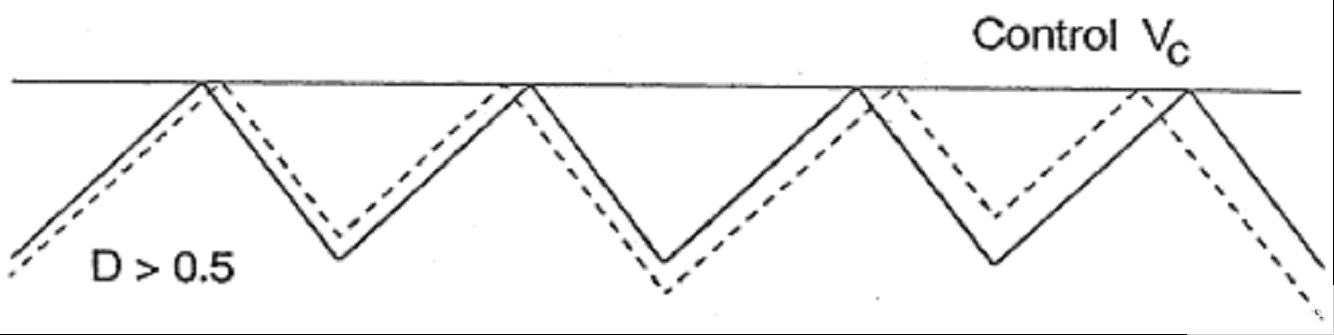
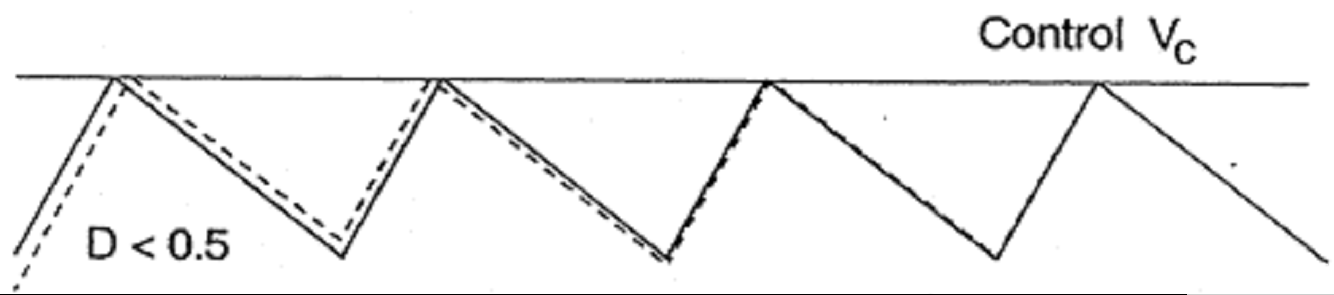
图 2.在占空比 D 《 0.5 和 D 》 0.5 时，感应到的电感器电流以 R i斜升

本节将介绍峰值电流模式降压转换器 ［1］ ［2］ 的小信号模型。V. Vorperian ［1］ 提出的 Buck PWM 开关模型和 Raymond B. Ridley ［2］ 提出的用于峰值电流模式控制的小信号模型如图 3 所示。根据该模型推导出的方程为应用于峰值电流模式降压转换器的补偿设计。

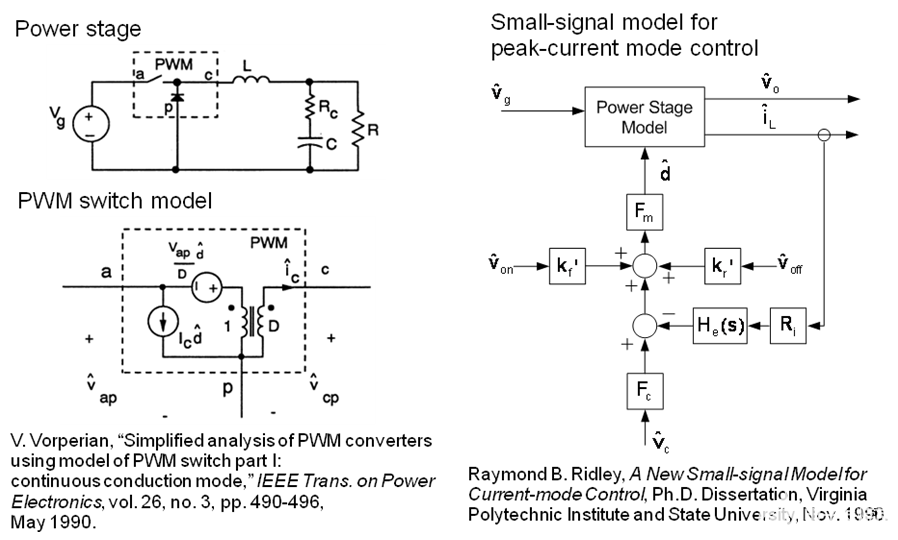
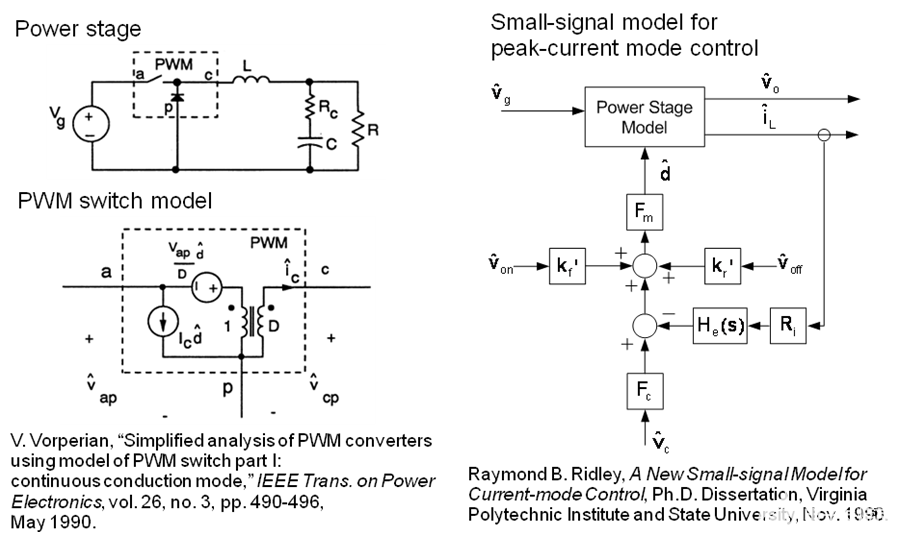
图 3. 用于峰值电流模式控制的降压 PWM 开关模型和小信号模型

下面列出了峰值电流模式降压转换器的开环传递函数 ［1］、［2］：

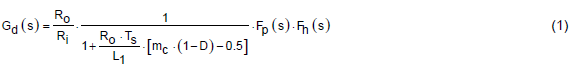
等式 （1） 中的F p （s） 主导了该配置的开环低频特性，如下所示，如等式 （2） 所示，它有一个零点和一个极点。

等式 （1） 中的F h （s） 表示该配置的高频特性，其中电流检测变压器 R i起重要作用。F h （s） 如下所述，如等式 （3） 所示，它具有两个高频极点。

图 4 显示了一个低频主极点（斜率为 -20dB/十倍频）和一个高频双极点（斜率为 -40dB/十倍频衰减）。两者之间的 ESR 为零来自输出电容器的 ESR。

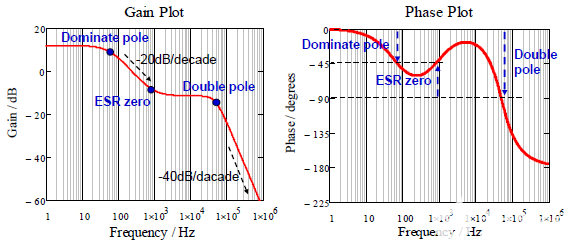
图 4. 开环峰值电流模式降压转换器的波特图

下面将逐步分析补偿设计的方程：

首先，精确的低频极点方程如下所示：

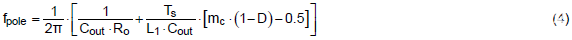
需要先进的计算工具来计算上述方程。然而，下面列出的简化方程是一个近似值，通过它可以快速找到极点。

下式为输出电容为零：

以下等式适用于双极点，位于开关频率的一半处：

通过上述公式，我们将提供一个设计示例来描述峰值电流模式降压转换器的重要特性。

图 5 显示了降压转换器的电路图和相应的电路参数。输入电压12Vdc，额定输出电流3A，输出电压3.3V，工作频率340kHz，电感10μH，输出电容44μF，ESR 5mΩ。

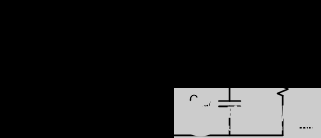
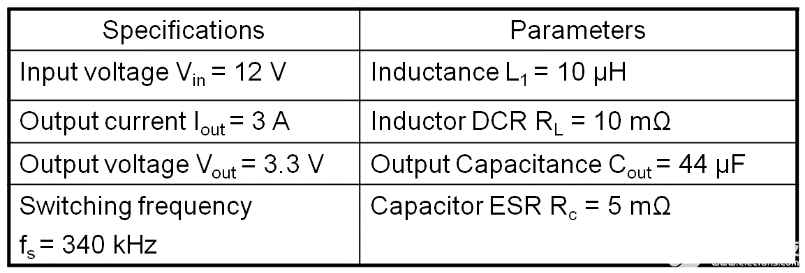
图 5. 峰值电流模式降压转换器的电路图和相应的电路参数。

将上述参数代入式（4），得到更准确的低频一阶极点，位于4.3kHz。

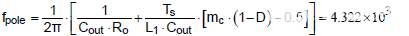
斜率补偿因子 m c定义为

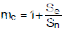
，其中 S e是添加的补偿锯齿斜坡的斜率，而 S n是开关打开时感测电流斜坡的斜率。

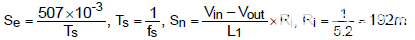
通过等式 （5），一阶极点 3.3kHz 可以很容易地计算如下。

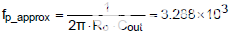
将上述参数代入式（6），可得到输出电容ESR归零的准确位置为723kHz。

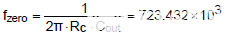
然后，通过等式（7），获得高频双极点为 170kHz。

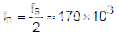
插入上述所有参数后，Mathcad 可以绘制如下波特图。在图 6 中，可以看出极点出现在低频 （3.28kHz） 处，而 ESR 零 （723kHz） 出现在比双极点更高的频率处，因为使用了较小的 ESR。

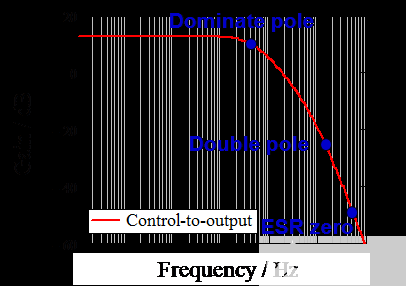
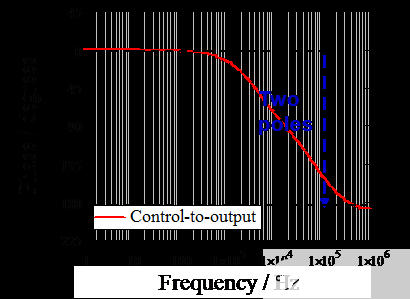
图 6. 设计实例中开环峰值电流模式降压转换器的波特图

2. 峰值电流模式降压转换器的补偿设计

上一节已经描述了峰值电流模式降压的特性。在本节中，将研究如何补偿峰值电流模式降压转换器以提高系统稳定性。在图 7 中，开环增益以红色绘制；在低频时，直流增益很低。低频下的低直流增益会导致稳态误差，如图 10 所示，图 9 显示了具有相同带宽和相位裕度的两种不同直流增益的频率响应。对于 f 》 f c，增益曲线斜率为-40dB/decade，相位曲线斜率为-90°/decade，往往导致相位裕度不足，如图8所示，进而导致系统不稳定。最佳闭环增益以蓝色绘制。与开环增益相比，闭环增益具有以下优点：低频时直流增益较高，稳态误差可以最小化，如图 10 所示，当 f 》 f c时，增益为-20dB/decade 的斜率和 -45°/decade 的相位，如图 7 所示，从而提高相位裕度 （PM）。

图 7. 开环和闭环波特图的比较

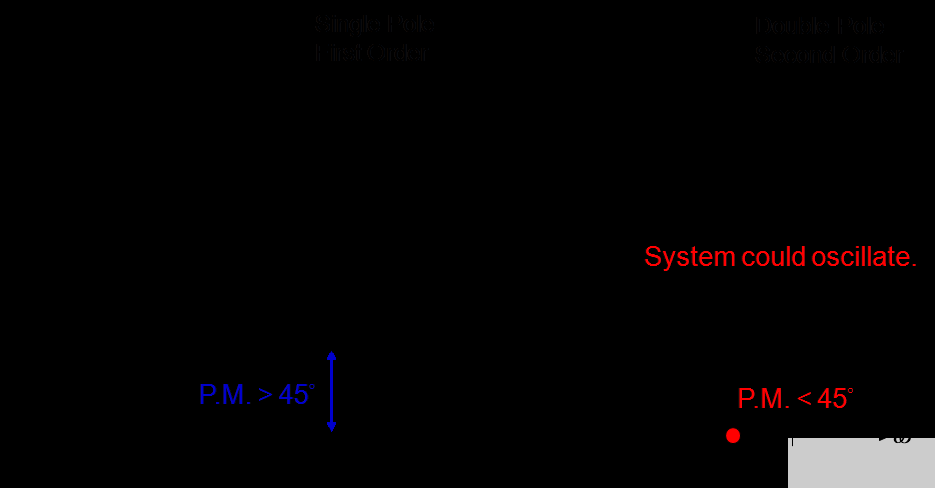
图 8. 单极与双极

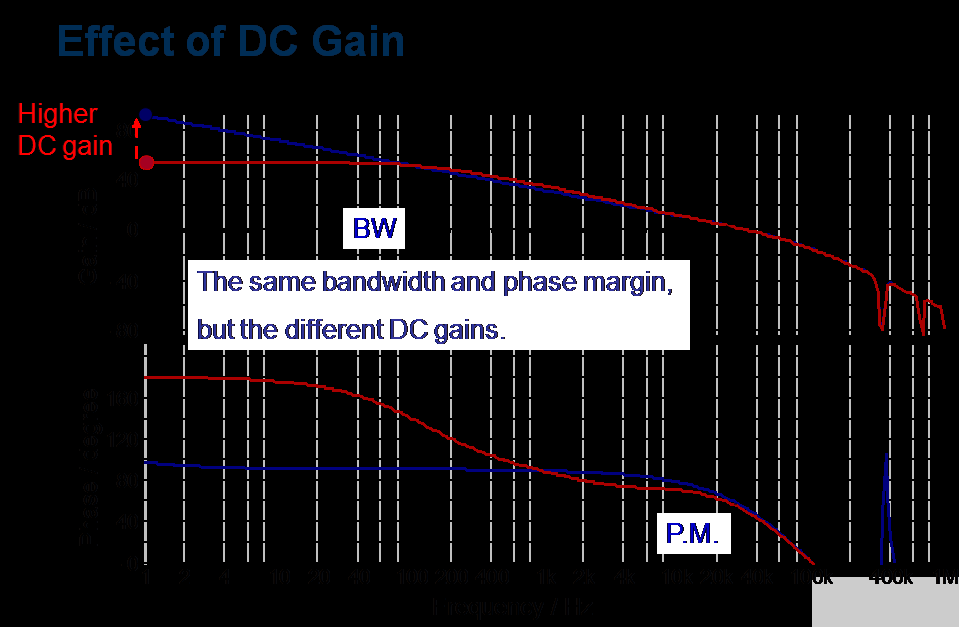
图 9. 具有相同带宽和相位裕度的不同 DC 增益

在图 10 中，可以看出负载调节率越高，直流增益越好，而直流增益越低，负载调节率越差。

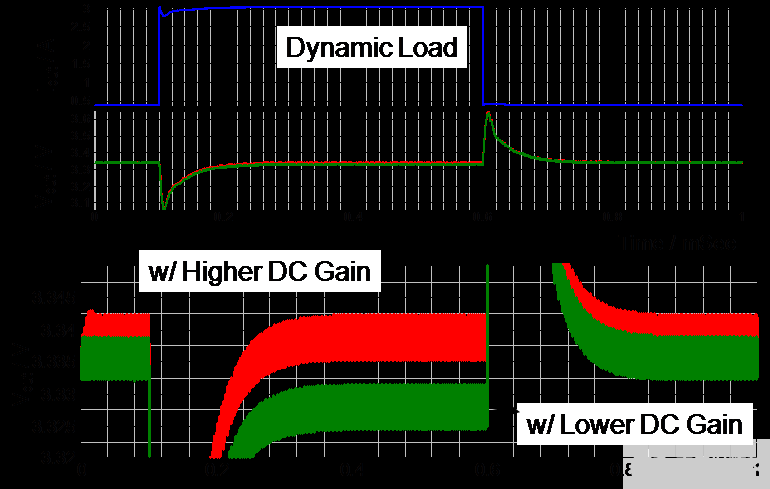
图 10. 直流增益对负载调节的影响

基于以上对系统性能电路参数的分析，补偿器需要一个零点来抵消峰值电流模式降压转换器的低频极点，如图 11 所示，这样增益曲线将是在交叉频率的斜率为 -20dB / 十倍频，从而获得更好的相位裕度。在高频下，高频补偿器极点可以帮助滤除高频噪声。

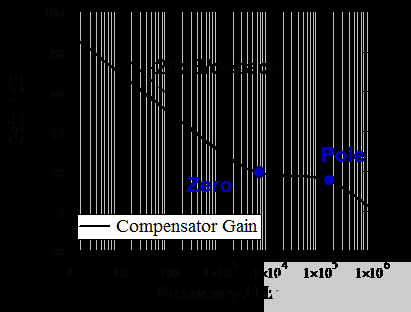
图 11. 补偿器提供零和极点

下面以 GM 型补偿器为例。由于 GM 型补偿器有一个零和两个极点，因此非常适合补偿峰值电流模式降压转换器。可以从 R gm和 C comp获得第一个极点，从 R comp和 C gm获得另一个极点，从 R comp 和 C comp获得零。

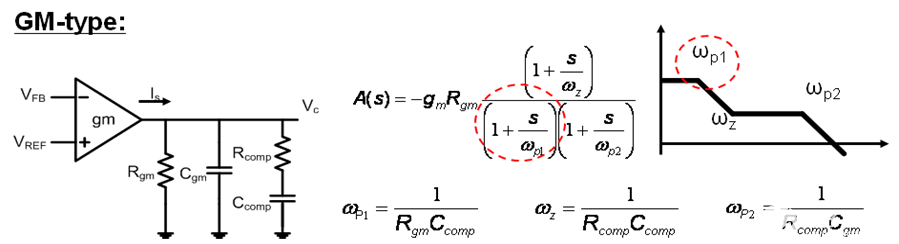
图 12. GM 型补偿器

补偿器设计程序：

第一步：

设置交叉频率（即带宽）。在上面的例子中，工作频率为 340kHz，带宽通常设置为工作频率的 1/10。

第 2 步：

将补偿器置零以取消峰值电流模式降压拓扑的极点。

步骤 3：

补偿器极点设置为 ESR 零和工作频率的 1/2 之间的较低频率。在本例中，工作频率的 1/2 低于 ESR 零，因此将补偿器极点设置为工作频率的 1/2。

步骤 4：

通过 Mathcad，48° 的相位裕度可以通过以下等式获得。通常为了稳定，相位裕度应大于 45°。

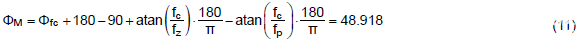
第 5 步：

根据等式 （12），由补偿器在交叉频率处增加的直流增益可计算为 17.4dB。

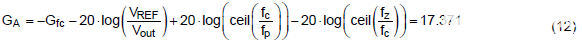
第6步：

本例中补偿器的参数，如R comp = 5.9kΩ，C comp = 6.23nF，C gm = 158pF，都可以得到如下。

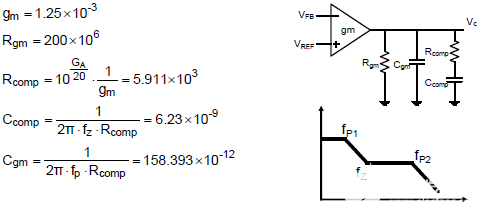
Step 7 ：

将上述所有数字代入式（13），然后将等式输入Mathcad，即可绘制出补偿器的Bode图，如图13所示。

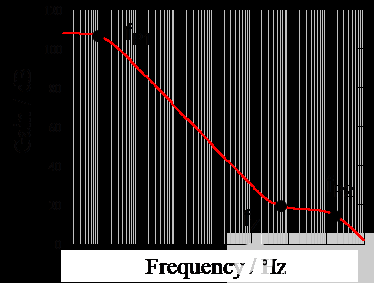
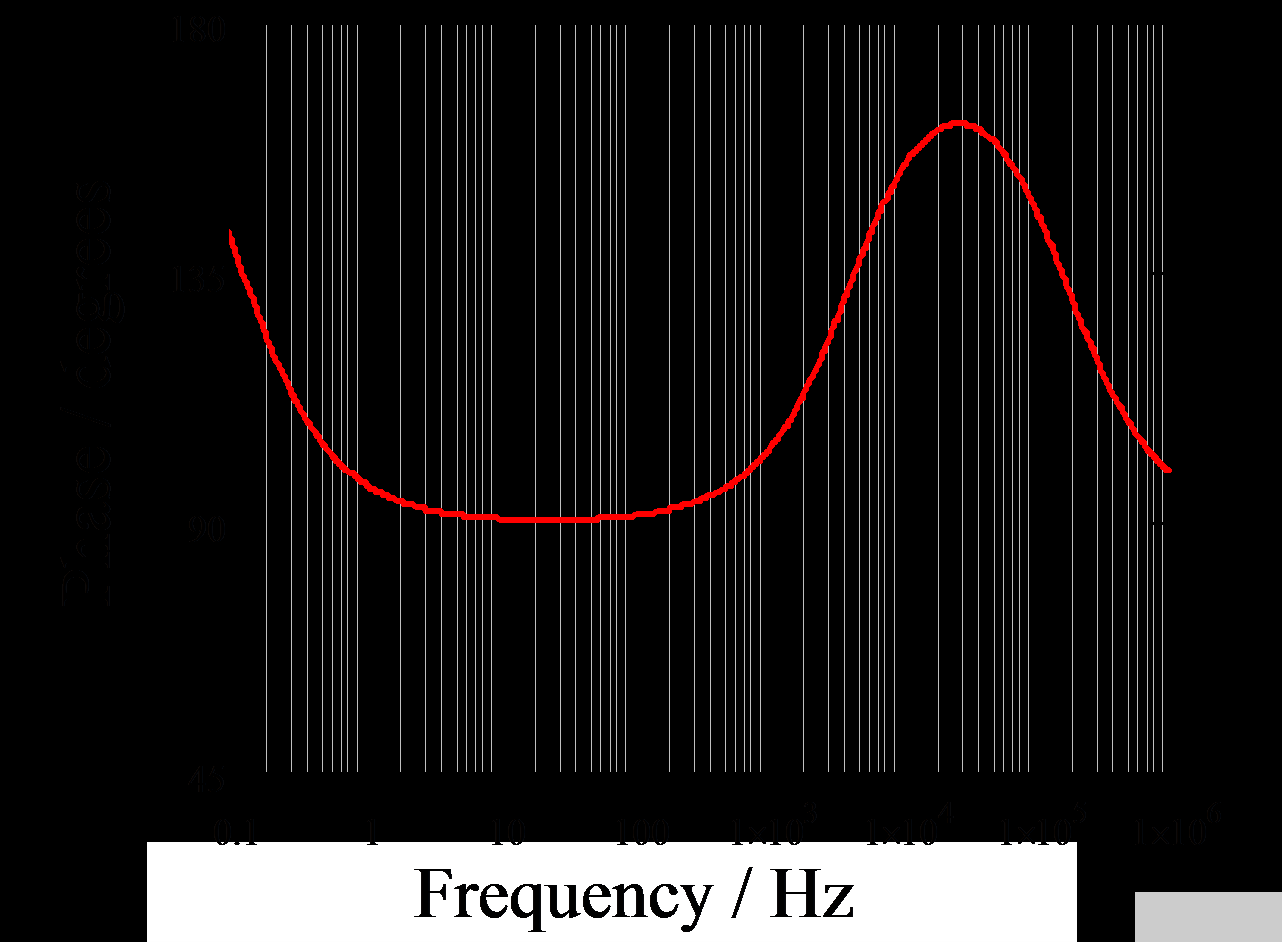
图 13. 补偿器的波特图

3. 峰值电流模式降压转换器的闭环分析

在本节中，SIMPLIS 工具用于模拟峰值电流模式降压转换器并证实闭环频率响应分析。SIMPLIS 原理图如图 14 所示。该电流模式降压转换器的闭环包含一个电流传感器、一个补偿器和一个斜率补偿电路。

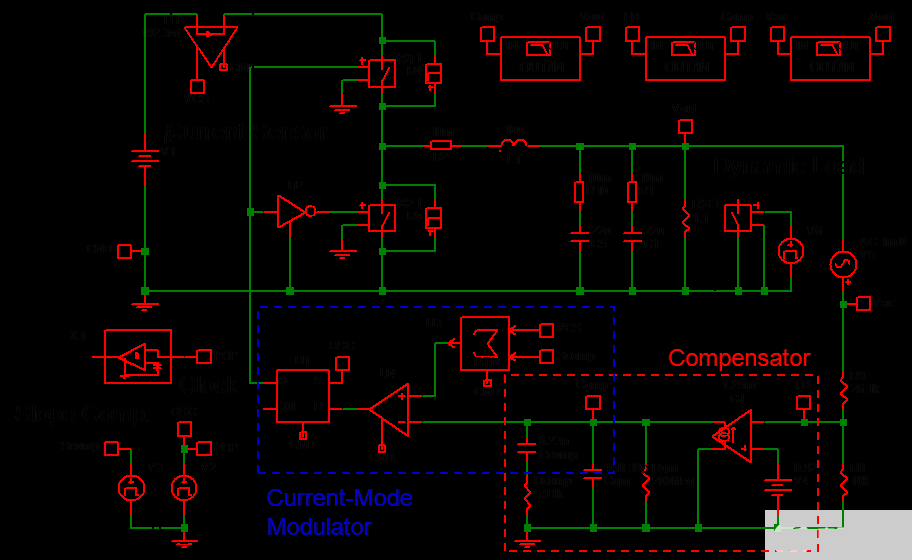
图 14. SIMPLIS 仿真示意图（闭环峰值电流模式降压转换器）

在图 15 中，上一节的方程（红线）由 Mathcad 绘制，并与图 14 中 SIMPLIS 原理图的仿真结果（蓝点）进行了验证。表明仿真结果与解析结果非常吻合，由 Mathcad 导出，带宽和相位裕度分别为 34kHz 和 48.9°。

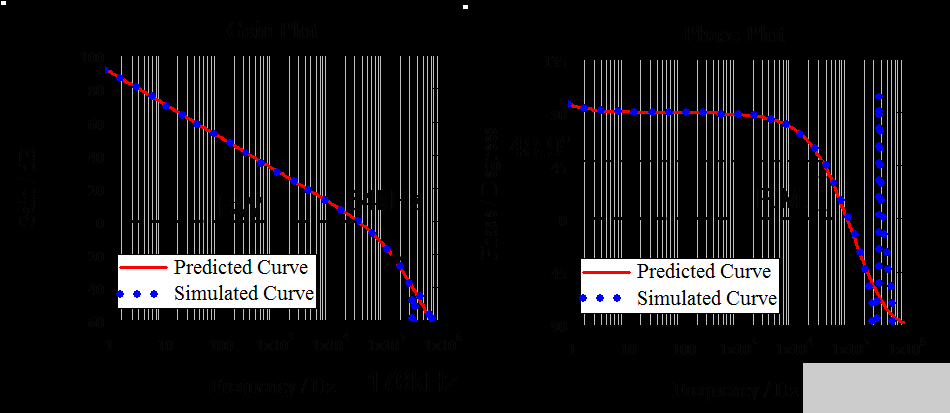
图 15. 理论分析与 Matchcad 和 SIMPLIS 仿真的比较

图 16 展示了补偿器可以提供的好处。首先，补偿器（黑色虚线）增强了低频范围内的直流增益。开环响应（红线）与补偿器响应（黑色虚线）相结合，形成闭环响应（蓝线）。其次，补偿器增加了带宽，如图 16 所示，蓝色的交叉频率大于红色的交叉频率。第三，补偿器增加了一个高频极点，提高了高频抗噪能力（在高频下，蓝线比红线下降得快）。第四，补偿器的零有助于实现足够的相位裕度。

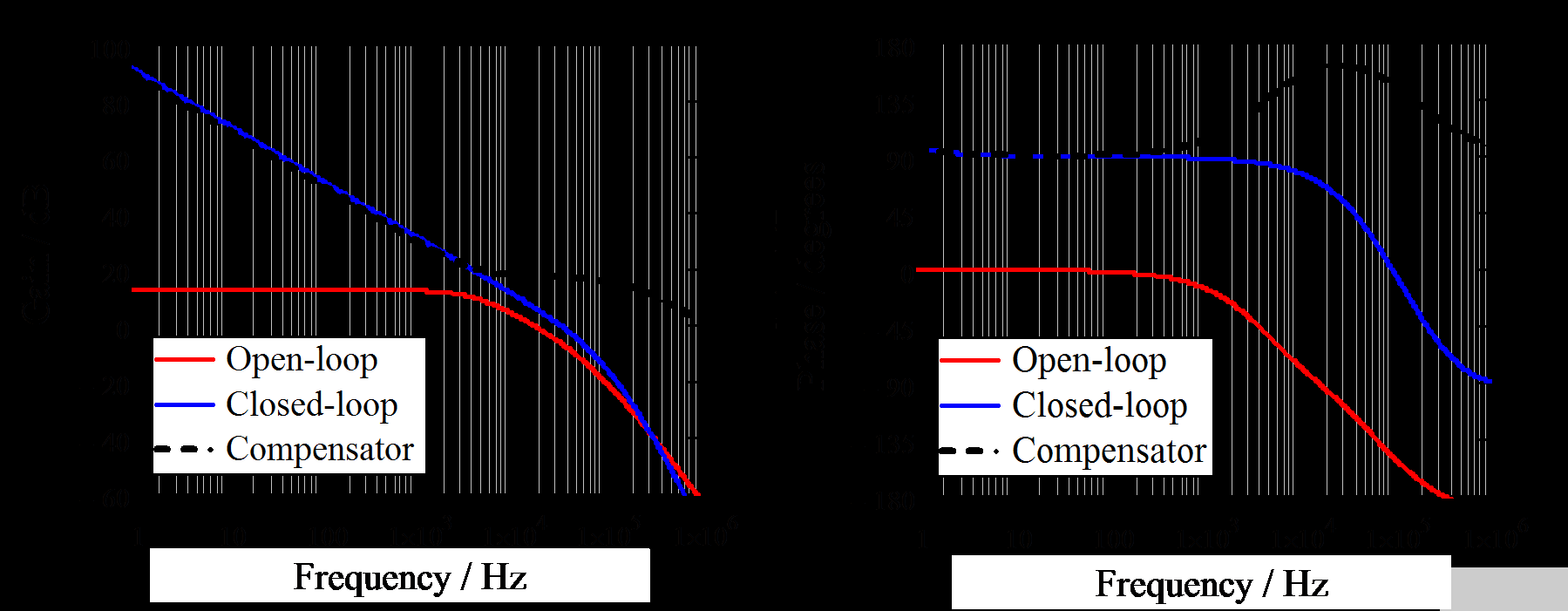
图 16. 开环和闭环的比较

图 17 给出了实际测量设置，将交流扰动信号注入点 R。通过测量输出（A 点）与输入（R 点）的关系，可以获得增益和相位图。从图 17 的右侧图中，测量结果（绿线）与分析结果（红线）非常吻合。

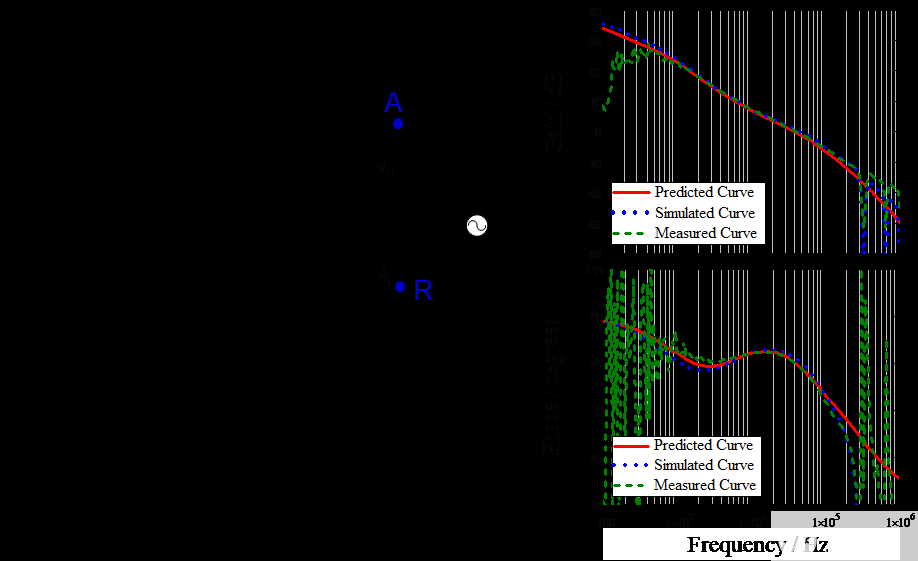
图 17. 实验结果验证闭环频率响应

4。结论

在低频下，开环峰值电流模式降压转换器仍然是单极点系统，因为环路控制是通过仅将电流信号注入环路来实现的。

它的补偿器易于设计。零补偿器旨在消除降压转换器的主极点，以实现系统稳定性。

为了保证足够的相位裕度，设计目标是增益曲线在通过交叉频率时在斜率-20dB/十倍频。