欧姆定律加基尔霍夫电流定律等于更好的人工智能

用模拟电路在存储器中进行神经网络处理将有助于节能。

机器学习和人工智能（AI）已经深入到日常生活和工作中，我们可能已经忘记与机器的交互曾经是什么样子。以前，我们通过数字键盘、电子表格或编程语言求得的都是精确的定量答案，比如“10的平方根是多少？”“按照这种利率，未来五年我的收益是多少？”等。 但在过去的10年里，我们已经习惯了机器回答那些只向他人提出过的模糊定性问题，比如“我会喜欢这部电影吗？”“今天的交通状况如何？”“这笔交易是否存在欺诈？”等。 深度神经网络（DNN）实现了这些新功能。深度神经网络是一种通过正确答案训练并学习如何对类似的新问题做出响应的系统，根据国际数据公司（IDC）的统计数据，深度神经网络是推动全球人工智能硬件、软件和服务市场快速增长的主要力量，去年该市场的估值为3275亿美元，预计到2024年将超过5000亿美元。 首先推动这场革命的是卷积神经网络，它提供了非凡的图像识别能力。在过去10年里，用于自然语言处理、语音识别、强化学习和推荐系统的深度神经网络新模型实现了许多其他的商业应用。 但不仅是应用数量在增长，网络规模和所需的数据也在增长。深度神经网络具有内在可扩展性——随着它们变大，训练数据增多，它们提供的答案也更加可靠。但这样做是有代价的。2010年至2018年间，训练最佳深度神经网络模型所需的计算增长了10亿倍，这意味着能耗大幅增加。虽然每次对已受过训练的深度神经网络模型使用新数据（称为“推理”）比训练深度神经网络模型本身所需要的计算量少得多，消耗的能量也少很多，但这种推理计算的数量非常大而且在不断增加。人工智能如果要继续改变人们的生活，就必须提高效率。 我们认为，可能需要从数字计算转变到模拟计算。利用非易失性存储设备和电气工程的两个基本物理定律，使用简单的电路就可以实现深度学习最基本的计算，而且只需要千万亿分之一焦耳的能量。在这项技术能够应用于复杂的人工智能之前，还有大量的工程工作要做，但我们已经取得了很大的进步，并规划出了一条前进的道路。

对大多数计算机来说，在外部存储器和计算资源（如CPU和GPU）之间移动大量数据耗费的时间成本和能源成本最高。这就是被称为“冯•诺依曼瓶颈”的存储与逻辑分离的经典计算机结构。要大大减少深度学习所需要的能量，有一种方法是避免移动数据，即在存储数据的地方进行计算。

深度神经网络由多层人工神经元组成。每一层神经元根据神经元的“激活值”和连接下一层神经元的突触“权值”这两个值驱动下一层神经元的输出。 大多数深度神经网络计算由向量矩阵乘法（VMM）运算组成，即向量（一维数字数组）与二维数组相乘。在电路级，这些运算为乘积累加运算（MAC）。对于每个下游神经元，所有上游激活值必须与相应的权值相乘，然后将这些乘积相加。 大多数有用的神经网络太大，无法存放在处理器内存中，计算每一层网络时，都必须从外部存储器导入权值，每一次计算都要受到冯•诺依曼瓶颈的束缚。这使得数字计算硬件更支持更少从存储器中移动权值并能积极重复使用这些权值的深度神经网络。

2014年，我们在IBM研究实验室提出了一种全新的深度神经网络硬件节能方式。我们和其他研究人员一直在研究非易失性存储器（NVM）设备的交错阵列。交错阵列是一种将器件（例如存储单元）构建在两组正交水平导体（即所谓的“位线”和“字线”）之间的垂直空间的结构。我们意识到，只要稍作修改，我们的存储系统将非常适合深度神经网络计算，尤其是那些现有权值重复使用效果不佳的计算。我们将这一机遇称为“模拟人工智能”，其他从事类似工作的研究人员也将其称为“存储计算一体化”（processing-in-memory）或“存内计算”（compute-in-memory）等。

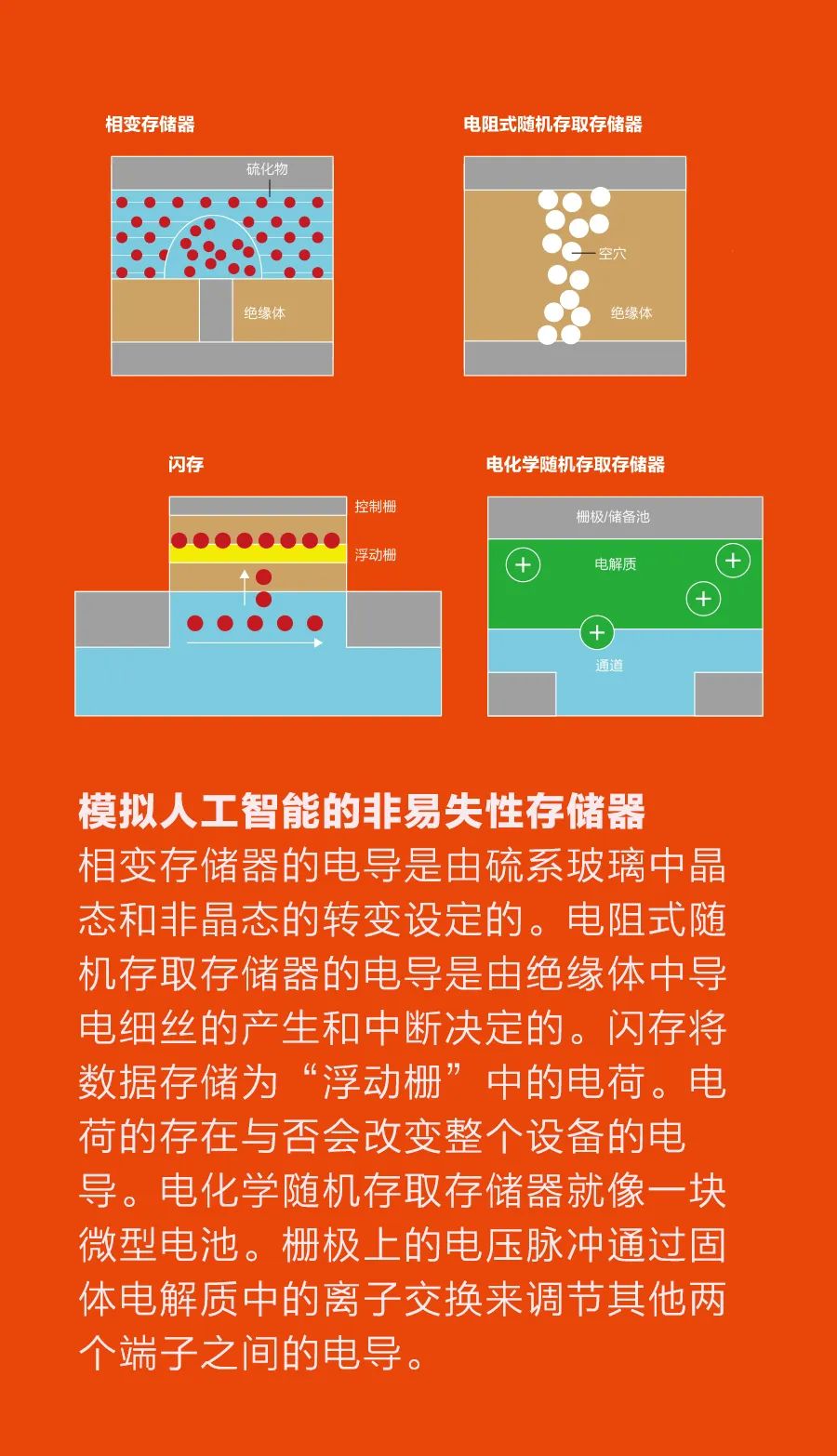
非易失性存储器有几种不同的类型，每种类型的数据存储方式不尽相同，但都通过测量设备的电阻（或者电阻倒数，即电导）从这些设备中读出数据。磁阻式随机存取存储器（MRAM）使用的是电子自旋，而闪存使用的是陷阱电荷。电阻式随机存取存储器（RRAM）设备通过在微小的金属-绝缘体-金属器件内产生并随后中断导电细丝来存储数据。相变存储器（PCM）利用热量在高导电晶相和低导电非晶相之间引发快速可逆的转换。 闪存、电阻式随机存取存储器和相变存储器能够提供传统数字数据存储所需的低电阻和高电阻状态，以及模拟人工智能所需的中间电阻。但在高性能逻辑中，只有随机存取存储器和相变存储器能够放置在硅晶体管上方布线的交错阵列中，将存储和逻辑之间的距离缩到最短。 我们将这些非易失性存储器存储单元组织在一个二维阵列中，称为“瓦片”（tile）。瓦片上有控制非易失性存储器设备读写的晶体管或其他器件。对于存储应用而言，读数电压寻址到一行（字线），会产生与非易失性存储器电导成正比的电流，在阵列边缘的列（位线）上可检测到这些电流，从而读出存储的数据。 为了让这样一个瓦片成为深度神经网络的一部分，每一行都需要用一个电压持续驱动一段时间，形成一个上游神经元激活值的编码。每一行的每个非易失性存储器设备则用其电导系数形成一个突触权值编码。通过欧姆定律（在这种情况下表示为“电流等于电压乘以电导”），产生的读电流就是励磁和权值的有效乘积。然后，根据基尔霍夫电流定律将每个位线上的各个电流相加。这些电流产生的电荷随时间积聚在电容器上，产生乘积累加运算结果。

这些相同的模拟存内求和方法也可以使用闪存甚至是静态随机存储器（SRAM）单元来执行。静态随机存储器单元可以存储多个数字位，但不能存储模拟电导值。虽然我们不能将欧姆定律用于乘法那一步，但是我们可以使用一种方法获取这些存储设备的一位或两位的动态范围。然而，这种方法对噪声非常敏感，因此我们在IBM一直坚持研究基于相变存储器和电阻式随机存取存储器的模拟人工智能。

与电导不同，深度神经网络权值和激活值可以为正，也可以为负。为了实现有正负之分的权值，我们使用了两条电流路径，一条向电容器添加电荷，另一条减去电荷。为了实现有正负之分的励磁，我们允许每行设备根据需要转换其连接路径。 每列每执行一次乘积累加运算，瓦片会并行执行整个向量矩阵乘法。对于一个具有1024×1024权值的瓦片，意味着一次执行100万次乘积累加运算。 在我们设计出来的系统中，我们预计所有这些计算只需32纳秒。由于每个乘积累加运算执行的计算相当于两次数字运算（一次乘法和一次加法），因此每32纳秒执行100万次模拟乘积累加运算代表着每秒65万亿次运算。 我们已制作出能够完成这一壮举的瓦片，每次运算仅用36毫微微焦耳能量（相当于每焦耳28万亿次运算）。而我们最新的瓦片设计将这一数字降到了10毫微微焦耳以下，其效率是商用硬件的100倍，比最新定制的数字加速器系统级能效高10倍，那些加速器为了能效甚至要牺牲精度。 对我们来说，提高每个瓦片的能效非常重要，因为一个完整的系统也会在其他任务上消耗能量，比如移动激活值和支持数字电路。

要使这种模拟人工智能方法真正取得成功，还有许多重要挑战需要克服。首先，根据定义，深度神经网络具有多层结构。要实现多层级联，我们必须通过人工神经元的激活作用（一种非线性函数）处理向量矩阵乘法瓦片的输出，并将其传递给下一个瓦片。非线性有可能通过模拟电路执行，并且以下一层所需的持续时间形式传达结果，但除了向量矩阵乘法的简单级联之外，大多数网络还需要其他运算。这意味着我们需要高效的模数转换（ADC），以及和瓦片之间进行适量的并行数字计算。新颖、高效的数模转换有助于避免这些电路对整体效率产生过多影响。最近，我们推出了一种基于相变存储器的高性能瓦片，使用了一种新型模数转换方法，可以帮助瓦片实现每瓦10万亿次以上的运算。

第二个挑战与非易失性存储器设备的特性有关，且更棘手。即使用相当低精度的数字描述它们的权值，数字深度神经网络的准确性也已经得到了证明。CPU经常使用的32位浮点数对深度神经网络是不必要的。使用8位浮点数甚至4位整数，深度神经网络通常也能工作得很好，能耗也很低。这为模拟计算带来了希望，只要我们能够保持类似的精度即可。

鉴于电导精度的重要性，需要将表示模拟神经网络中的权值的电导值慢慢地、仔细地写入非易失性存储设备。与传统存储器（如静态随机存取存储器和电阻式随机存取存储器）相比，相变存储器和电阻式随机存取存储器的编程速度较慢，几个编程周期后会出现磨损。幸运的是，推理不需要经常重新编程权值。因此，模拟人工智能可以使用耗时的写验证技术来提高相变存储器和电阻式随机存取存储器的编程精度，且不必担心设备磨损。 这种提升是非常必要的，因为非易失性存储器具有内在的编程噪声。电阻式随机存取存储器的导电性取决于几个原子形成细丝的运动；相变存储器的导电性取决于多晶材料中晶粒的随机形成。这两种随机性给数值的写入、验证和读取带来了挑战。此外，在大多数非易失性存储器中，电导会随温度和时间而变化。除此之外，还有相变存储器中的非晶相结构漂移、电阻式随机存取存储器中的细丝松弛或闪存单元中捕获的电荷泄漏等影响。

有几种方式可以巧妙地解决这个问题。使用两个电导对可以显著改善权值编程问题。其中，一对用于保存大部分信号，而另一对用于纠正主对上的编程错误。由于噪声在多个设备间平均，所以噪声降低了。

我们最近对基于多相变存储器的芯片测试了这种方法，每个权值使用一个和两个电导对。我们用这种方法在多个深度神经网络上证明了其具有卓越的准确性，甚至包括通常对权值编程错误很敏感的循环神经网络。 不同的技术可以帮助改善读数噪声和漂移效应。但由于漂移是可预测的，也许最简单的方法是在读数过程中用与时间相关的增益来放大信号，这能够抵消大部分误差。另一种方法是开发同一技术，训练深度神经网络适应低精度数字推理。这些方法可调整神经网络模型以匹配底层硬件的噪声局限。 正如我们提到的，网络正变得很庞大。在数字系统中，如果网络与加速器不适配，你可以从外部存储芯片给每层深度神经网络导入权值。但是非易失性存储器的写入限制使得这一机制变得很糟糕。不过，可将多个模拟人工智能芯片组合在一起，将部分网络的中间结果从一块芯片传递到下一块芯片。这种机制会带来一些额外的通信延迟和能耗，但其代价远远小于本身移动权值。

到目前为止，我们只讨论了推理，即将新数据作用于已经过训练的神经网络。但是，模拟人工智能还有帮助训练深度神经网络的其他机会。

深度神经网络训练使用的是反向传播算法。它结合了成熟的正向推理运算和另外两个重要步骤——误差反向传播和权值更新。误差反向传播就像反向运行推理一样，由网络的最后一层到第一层；权值更新将运行原始正向推理的信息与这些反向传播误差结合起来，调整网络权值，使模型更加准确。 反向传播步骤可以在瓦片上进行，但与推理的方式相反——按列施加电压，按行积累电流。更新权值则是用正向推理的原始激活数据驱动行，同时使用反向传播期间产生的误差信号驱动列。 训练涉及必须消除的众多微小权值增减，但实现起来很困难，原因有两个。首先回想一下，非易失性存储器会因编程太多而产生损耗。其次，相同的电压脉冲以相反极性施加给非易失性存储器，存储单元的电导变化量可能不同；它的反应是不对称的。但是，对称特性对于反向传播产生精确网络而言至关重要。由于训练所需的电导变化幅度接近非易失性存储器材料的固有随机水平，这将变得更具挑战性。 有几种办法可以帮助解决这方面的问题。例如，有许多方法可累积多个训练案例的权值更新，然后在训练期间定期将这些更新传输给非易失性存储设备。我们在IBM开发了一种叫做“Tiki-Taka”的新算法，通过这种技术，成功使用高度不对称的电阻式随机存储设备对深度神经网络进行了训练。最后，我们正在开发一种名为“电化学随机存取存储器”（ECRAM）的设备，它可以提供不仅对称而且高度线性和渐进的电导更新。

模拟人工智能能否成功将取决于能否同时实现高密度、高吞吐量、低延迟和高能效。密度取决于非易失性存储器集成到芯片晶体管上方布线的紧密程度。瓦片级别的能源效率将受到模数转换电路的限制。

但是，即使这些因素得到改善，越来越多的瓦片连接在一起，阿姆达尔定律（关于并行计算局限性的论点）也将对系统能效优化提出新的挑战。先前不是特别重要的内容，如瓦片之间所需的数据通信和剩余的数字计算，将产生越来越高的能耗预算，导致瓦片本身的峰值能源效率与整个模拟人工智能系统的持续能源效率产生差距。当然，无论模拟还是数字人工智能，每一个人工智能加速器最终都将面临这个问题。

前进的道路必然与数字人工智能加速器不同。数字的方法可降低精度，直到准确性衰降。但是，模拟人工智能必须首先提高内部模拟模块的信噪比（SNR），直到足以证明其与数字系统的准确性相当。信噪比提高以后，可改进提高密度和能源效率。

这些令人振奋的问题都需要解决，而解决这些问题需要材料科学家、设备专家、电路设计师、系统架构师和深度神经网络专家的共同努力。人们对更节能的人工智能加速器有强烈且持续的需求，同时又没有其他有吸引力的替代方式来满足这一需求。考虑到各种各样的潜在存储设备和实现途径，某种程度的模拟计算很可能会进入未来的人工智能加速器。

审核编辑 ：李倩