自主或与人类工人一起操作的机器人设计提供了便利、效率和准确性,极大地造福了制造业和工业部门。在这里,在所有条件下监控电机位置有助于保持系统控制并防止可能导致系统损坏或人身伤害的意外运动。
为此,可以使用安装在电机轴上的磁铁为磁性编码器提供输入,从而实现非接触式角度编码。磁场不受污垢或污垢的影响,将此类解决方案集成到电机上可实现紧凑的解决方案。编码器跟踪旋转磁场分量,这些分量是自然正弦曲线和 90 度异相。这种关系可以使用这些输入的反正切快速计算角度位置。
多种磁编码技术将具有相同的最终效果。当磁铁在电机轴上旋转时,磁阻和霍尔效应传感器可以检测到不断变化的磁场。3D 线性霍尔效应传感器等器件能够计算角位置并提供补偿温度漂移、不平衡输入幅度以及器件灵敏度和偏移的能力。
除了信号链误差之外,机械公差也会影响磁体的旋转,这反过来又会决定检测到的磁场的质量。实现最佳性能通常需要通过多点线性化或谐波逼近来实施最终校准过程。一旦针对机械误差源进行了校准,磁编码就可以实现高精度。
驱动电机可以直接旋转负载,驱动齿轮箱以增加施加的扭矩,控制齿条和小齿轮,或通过皮带或螺杆传动将能量转移到其他地方。随着电机的轴旋转,动能转移到系统某处的机械位置变化中。无论如何,电机轴的角度与机构运动部件的位置直接相关。在匝数比不是 1 比 1 的情况下,跟踪电机转数也变得很重要。
位置计算
观察两个相差 90 度的等幅正弦输入,并使用这些信号执行反正切计算,从而跟踪电机的绝对角度。
下面概述的技术可以计算角位置:
步进电机和无传感器电机控制不提供绝对位置反馈,而是根据起始位置的相对变化来估计位置。当系统断电时,必须通过其他方式确定电机的实际位置。
对于列出的其余技术,角度编码器使用具有 90 度相位差的正弦输出来确定精确的角度位置。
光学编码器往往提供最高精度的精度,但通常需要笨重的外壳来保护传感器和光圈免受灰尘、污垢和其他污染物的影响。此外,编码器的机械元件必须耦合到电机轴。高于编码器机械额定值的转速可能会导致无法修复的损坏并导致停机。
霍尔效应传感器和磁阻传感器等磁感应技术使用固定在电机轴上的磁铁;传感器不需要任何机械连接。与永磁体相关的磁场将渗透到磁体周围的区域,这为传感器放置提供了广泛的自由度。旋转磁体的磁场矢量分量自然有 90 度异相,这使得单片多轴磁传感器能够通过单个设备执行角度编码。紧凑的解决方案、放置自由度和非接触式配置使磁传感器对角度编码应用具有吸引力。
感应式传感器的工作原理与磁性解决方案类似,通过耦合感应线圈产生的交流磁场,在附近的金属目标中产生表面涡流。目标的接近度变化导致系统有效电感的变化,当与专用目标一起使用时,可以产生正弦和余弦输出。
让我们考虑由磁铁在TMAG5170等 3D 霍尔效应传感器上方旋转产生的理想输入,如图 1所示。
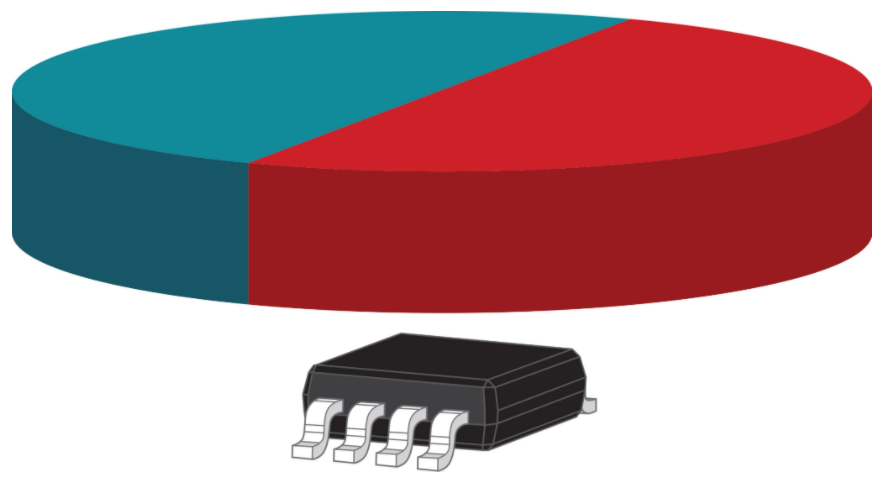
图 1同轴磁旋转允许霍尔效应传感器计算角位置。资料来源:德州仪器
使用输入的反正切计算角度,如图 2所示,将提供对实际电机角度的完美推论,假设没有机械公差的理想布置。在实践中,有几个机械因素会影响磁场输入的质量。由此产生的角度误差将成为这些因素中每一个的复杂组合,具体取决于每个机械缺陷的严重程度。

图 2理想的正弦和余弦输入为实际电机角度提供了完美的推论。资料来源:德州仪器
现在,让我们看看影响性能的几种类型的装配错误。尽管同轴对齐往往是最宽容的,但每种方法的效果都会因传感器位置和磁体几何形状而异。
磁铁倾斜
如果磁铁没有完全垂直于其电机轴安装,则该磁铁在旋转过程中会出现摆动。磁铁的有效 XYZ 坐标空间与传感器的不一致对齐将导致角度测量非线性。

图 3磁铁倾斜(上)和摆动(下)会导致角度测量的非线性。资料来源:德州仪器
磁铁偏心率
在磁体旋转过程中,磁体相对于传感器的位置会不断变化。由于来自磁体的磁通密度与距离的平方成反比,因此这种效应会产生显着的非线性。结果,磁体的偏心可能是由于磁体与轴的旋转轴线的不正确对准而导致的。

图 4偏心磁体旋转是由于磁体对齐不当造成的。资料来源:德州仪器
系统位置偏移
放置偏移会在输入磁场分量的幅度和相位中引入意想不到的变化。这些误差同样会影响最终的角度计算。
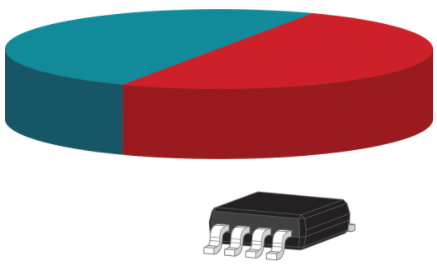
图 5偏移传感器放置可能会导致输入磁场的幅度和相位发生意外变化。资料来源:德州仪器
电机轴倾斜
根据磁铁的倾斜和用于计算的灵敏度轴,电机轴倾斜会导致输入信号相位误差。当使用反正切进行计算时,这种相位误差会产生非线性。在这种情况下,磁铁不会摆动,但传感器的正交性会丢失。

图 6倾斜电机校准会导致相位误差。资料来源:德州仪器
传感器焊接错位
这种情况与电机轴倾斜非常相似。在焊料回流期间,任何设备都可能在焊料凝固时无法完美对齐。这种未对准可能导致封装沿任何轴倾斜,这将导致输入可能出现幅度或相位误差。

图 7传感器未对准会导致幅度或相位误差。资料来源:德州仪器
纠正机械错误
图 8至图 11显示了与以原点为中心的理想圆相比的各种非线性误差的简单形式。这些图描绘了在绘制两个输入信号相互对比时各种错误的可能影响。
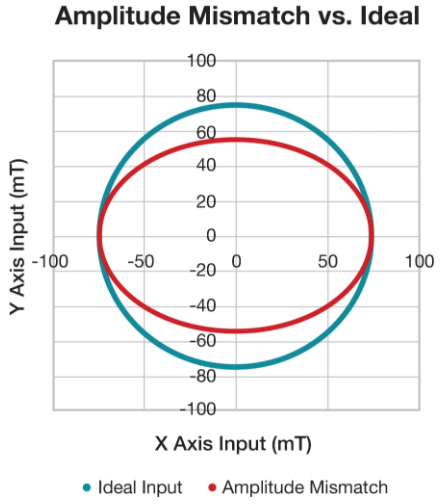
图 8这是理想输入(蓝色)和幅度失配(红色)之间的比较。资料来源:德州仪器
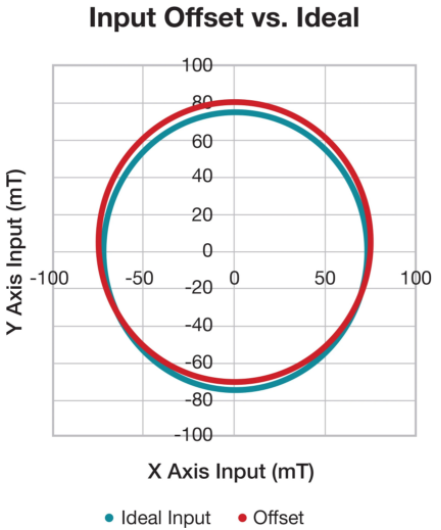
图 9显示了偏移和理想输入之间的比较。资料来源:德州仪器
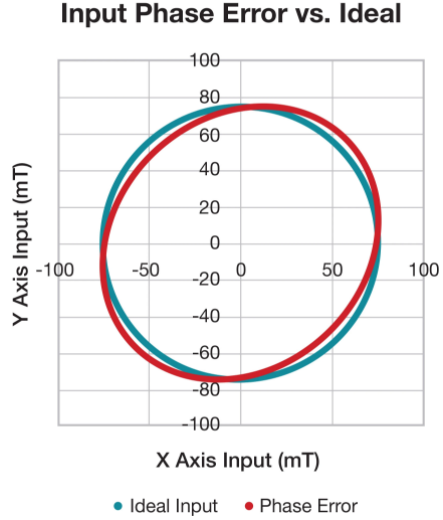
图 10显示了理想输入和相位误差之间的比较。资料来源:德州仪器
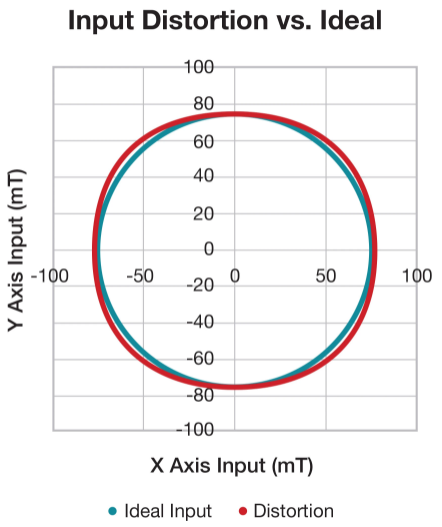
图 11显示了失真和理想输入之间的比较。
在方程式 1 中,θ' 表示计算的角度。理想 90 度的相位误差显示为 σ。A(θ) 和 B(θ) 在理想情况下是等效函数,但也可以描述简单的标量幅度失配或由磁体旋转缺陷引起的幅度的周期性变化。变化幅度会导致失真,从而对角度线性度产生不利影响。
θ' = atan (A(θ) sin (θ+σ) + 偏移量sin )/(B(θ) cos (θ) + 偏移量cos ) (1)
取 θ 和 θ' 之间的差值来计算总是周期性重复的绝对角度误差。图 12中显示的误差是由未放置在轴上的传感器捕获的不匹配输入幅度产生的未校正误差的示例。
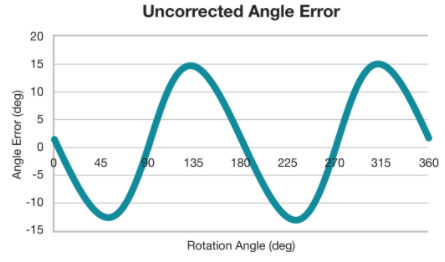
图 12这是由非理想磁输入引起的角度误差示例。资料来源:德州仪器
如果将传感器放置在轴上对齐,则任何幅度失配都将最小化,并且校正前的误差将具有较小的峰值。
幅度失配是由于传感器放置在磁场内造成的,但也可能受到传感器灵敏度增益误差的影响。调整通道灵敏度或在后处理中应用标量是标准化输入幅度的两种方法。
观察到的磁场中的信号链偏移或偏移也需要校正受影响的输入信号。执行这两种校正将立即提高整体准确性。
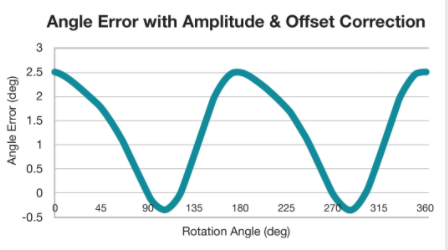
图 13剩余角度误差可能由机械源引起。资料来源:德州仪器
在解决幅度和偏移误差之后,剩余部分可归因于相位误差和失真。通常由机械未对准引起,此类误差在系统之间往往是独一无二的,并且更难以直接纠正。
校准方法
实施终端校准有两种常见的过程:多点线性化或谐波逼近。这两个过程都需要根据已知参考捕获多个数据点,以有效计算循环误差。
多点线性化假设每个收集的数据点之间存在线性变化。增加样本数量会降低这种近似的不确定性。考虑用四个、八个、16 或 32 个线性化点来校正图 13中所示的剩余误差。当应用于图 13 中所示的误差时,使用 32 个点的这种方法的残差在所有位置都远低于 0.1 度。
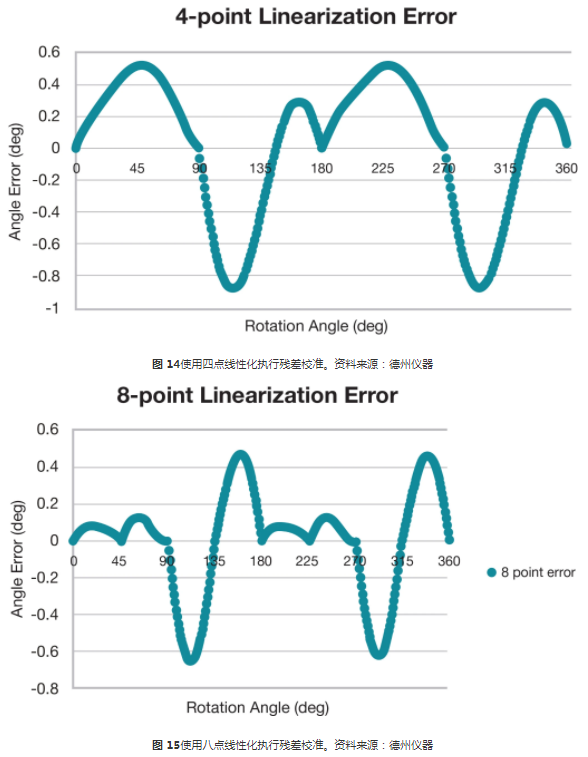
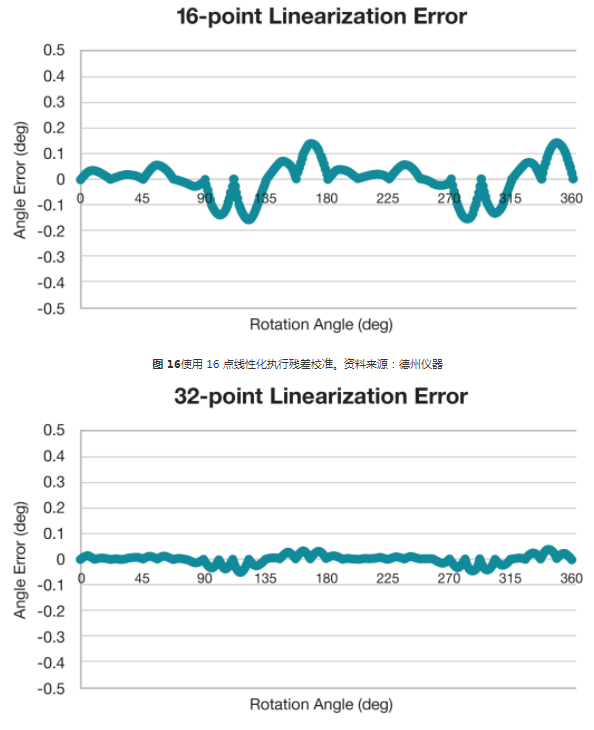
图 17使用 32 点线性化执行残差校准。资料来源:德州仪器
另一方面,谐波近似是一种先进的方法,可以识别误差的循环重复性质。等式 2 将总误差描述为谐波的无限组合之和:
θ 校正 = ∑ n i=1 α i cos (i * θ) + β i sin (i * θ) (2)
增加用于校准的数据点数量可以更准确地确定每个谐波的标量 α 和 β,从而产生比多点线性化更高的精度。
因此,不是使用分段线性化,而是通过仅减去前四个谐波来校正图 13 中的误差会导致所有位置的误差小于 0.01 度。
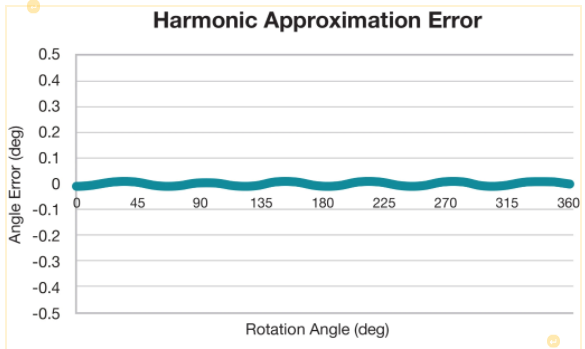
图 18这是使用谐波近似完成的误差校准的总体视图。资料来源:德州仪器
机器人中的磁感应
磁性角度传感是用于精密机器人应用的有益技术。虽然磁场渗透空间,但它提供了一种简单的方法来向微处理器提供角度信息,而无需直接机械连接到电机轴,从而减少可能导致系统故障的机制。
任何磁感应解决方案的挑战是可能的对齐因素和导致周期性角度误差的信号链误差的数量。仔细的设计可以限制这些错误的严重性,但总会存在一些系统容差。未经校准的所有这些来源的组合可能会导致不可接受的精度。多点线性化或谐波逼近提供了一种直接有效的方法来计算最高精度的电机位置。
德州仪器 (TI) 位置传感产品系统工程师 Scott Bryson 为 Planet Analog 撰写了 Signal Chain Basics 博客 # 175。
-
传感器
+关注
关注
2557文章
51893浏览量
759947 -
机器人
+关注
关注
212文章
29049浏览量
210208
发布评论请先 登录
相关推荐





 用于机器人中的磁性位置传感技术
用于机器人中的磁性位置传感技术










评论