拟或 合成数据 生成是人工智能工具发展的一个重要趋势。传统上,这些数据集可用于解决低数据问题或边缘情况场景,而或许现在存在于可用的实际数据集中。
合成数据的新兴应用包括建立模型性能水平、量化适用领域,以及下一代系统工程,其中人工智能模型和传感器是串联设计的。

图 1 。 船舶合成孔径雷达渲染: 相位图 ( left ) ,压缩图像 ( right )。
Blender 是生成这些数据集的一个常用且引人注目的工具。它是免费使用和开源的,但同样重要的是,它可以通过强大的 Python API 完全扩展。 Blender 的这一特性使其成为视觉图像渲染的一个有吸引力的选择。因此,它已被广泛用于此目的,有 18 +渲染引擎选项可供选择。
集成到 Blender 中的渲染引擎(如 Cycles )通常具有紧密集成的 GPU 支持,包括最先进的 NVIDIA RTX 支持。但是,如果在可视化渲染引擎之外需要高性能级别,例如合成 SAR 图像的渲染,那么 Python 环境对于实际应用程序来说可能过于迟缓。加速这段代码的一个选择是使用流行的 Numba 包将 Python 代码的部分预编译成 C 。然而,这仍有改进的余地,特别是在采用领先的 GPU 体系结构进行科学计算方面。
GPU 科学计算功能可直接从 Blender 中获得,允许使用简单的统一工具,利用 Blender 强大的几何体创建功能以及尖端计算环境。对于 blender2 。 83 +的最新变化,可以使用 CuPy (一个专门用于数组计算的 GPU 加速 Python 库)直接从 Python 脚本中完成。
根据这些想法,下面的教程将比较两种不同的加速矩阵乘法的方法。第一种方法使用 Python 的 Numba 编译器,而第二种方法使用 NVIDIA GPU-compute API, CUDA 。这些方法的实现可以在 rleonard1224/matmul GitHub repo 中找到,还有一个 Dockerfile ,它设置了 anaconda 环境,从中可以运行 CUDA – 加速的 Blender Python 脚本。
矩阵乘法算法
作为讨论用于加速矩阵乘法的不同方法的前奏,我们简要回顾了矩阵乘法本身。
对于两个矩阵的乘积[A*B]为了更好地定义[A]必须等于[B].
[A]然后是一个矩阵[m]行和[n]列,即[m*n]matrix.
[B]是一个[n*p]matrix.
产品[C=A.B]结果是[m*p]matrix.
如果[C],[A],和[B]使用数字 1 (即基于 1 的索引)进行索引,然后是的第 i 行和第 j 列中的元素[C],[C[i,j]],
由以下公式确定:
麻木加速度
通过使用 Numba 。 jit decorator ,可以将 Numba 编译器应用于 Python 脚本中的函数。通过预编译到 C 中,在 Python 代码中使用 numba 。 jit decorator 可以显著减少循环的运行时间。由于直接转换为代码的矩阵乘法需要嵌套 for 循环,因此使用 numba 。 jit decorator 可以显著减少用 Python 编写的矩阵乘法函数的运行时间。 matmulnumba.py Python 脚本实现矩阵乘法并使用 numba 。 jit decorator 。
CUDA 加速度
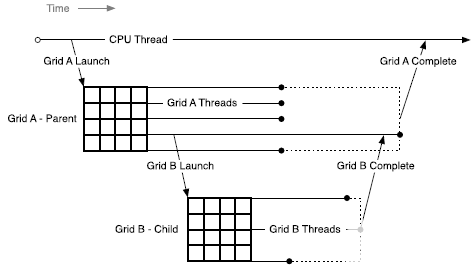
在讨论使用 CUDA 加速矩阵乘法的方法之前,我们应该大致概述 CUDA 内核的并行结构。内核启动中的所有并行进程都属于一个网格。网格由块数组组成,每个块由线程数组组成。网格中的线程组成了由 CUDA 内核启动的基本并行进程。图 2 概述了这类并行结构的示例。

图 2 。 一个由 2 组成的 CUDA 核网格的并行结构× 2 块数组。每个块由一个 2 × 2 个线程阵列。
既然已经详细说明了 CUDA 内核启动的并行结构,那么在 matmulcuda.py Python 脚本中用于并行化矩阵乘法的方法可以描述如下。
假设以下由一个由块的二维数组组成的 CUDA 内核网格计算,每个块由线程的一维数组组成:
矩阵积[C=A.B]
[A]and[m*n]matrix
[B]and[n*p]matrix
[C]and[m*p]matrix
此外,进一步假设如下:
网格 x 维中的块数 ([nblocksx]) 大于或等于[m]([nblocksx≥m])。
网格 y 维中的块数 ([nblocksy]) 大于或等于[p]([nblocksy≥p])。
每个块中的线程数 ([ntheads]) 大于或等于[n]([ntheads≥n])。
矩阵积的元素[C=A.B]可以通过为每个块分配一个元素的计算来并行计算[C],[C[i,j].
您可以通过将指定给要执行的块的每个线程来获得进一步的并行增强[C],[C[i,j]分配,计算[n]和等于[C],[C[i,j].
为了避免竞争条件,这些[n]积和结果的赋值[C],[C[i,j]可以使用 CUDA atomicAdd 函数处理。 atomicAdd 函数签名由作为第一个输入的指针和作为第二个输入的数值组成。该定义将输入的数值与第一个输入所指向的值相加,然后将该和存储在第一个输入所指向的位置。
假设[C]初始化为零[tid(i,j)]表示属于块的线程的线程索引,其索引在块的网格中[(i,j)]. 上述平行排列可通过以下方程式进行总结:
图 3 总结了两个样本矩阵乘法的并行排列[2*2].
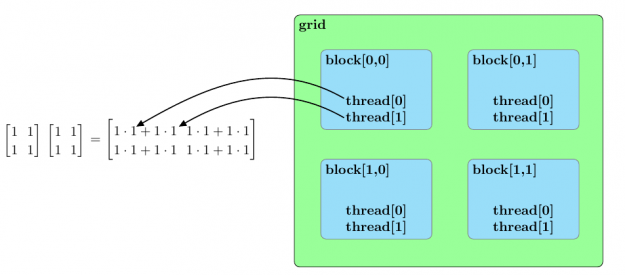
图 3 。两个 2 的乘法的并行化方法× 2 个矩阵。每个块被分配两个矩阵乘积的一个元素,一个线程块中的线程并行地计算乘积,以确定分配给块的矩阵元素的值。
提速
图 4 显示了 CUDA 加速矩阵乘法相对于不同大小矩阵的 Numba 加速矩阵乘法的加速比。在该图中,绘制了加速比以计算两个[N*N]两个矩阵的所有元素都等于一的矩阵。[N]范围从一百到一千,增量为一百。
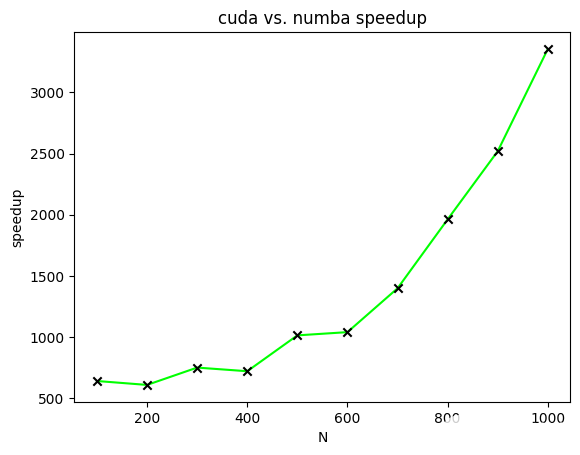
图 4 。两个 NxN 矩阵相乘时 CUDA 加速矩阵相乘相对于 Numba 加速矩阵相乘的加速比。
今后的工作
考虑到 Blender 作为计算机图形工具的作用,一个适用于 CUDA 加速的相关应用领域涉及到通过光线跟踪解决可见性问题。可见性问题可以概括如下: 相机存在于空间的某个点上,并且正在观察由三角形元素组成的网格。可见性问题的目标是确定哪些网格元素对摄影机可见,哪些网格元素被其他网格元素遮挡。
光线跟踪可以用来解决可见性问题。您试图确定其可见性的网格由[N]网格元素。那样的话,[N]可以生成以场景中的摄影机为原点的光线。这些端点位于[N]网格元素。
每条光线在不同的网格元素上都有一个端点。如果光线到达其端点时未被其他网格元素遮挡,则可以从摄影机中看到端点网格元素。图 5 显示了这个过程。
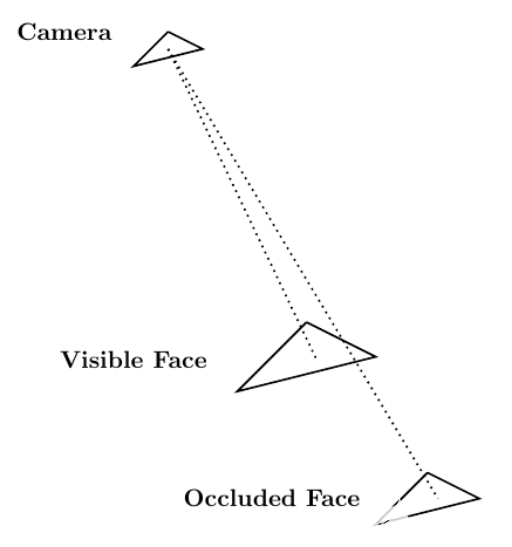
图 5 。 从相机向场景中的人脸发射的两条光线;一个面可见,另一个面被遮挡。
使用光线跟踪来解决可见性问题的本质使其成为
作为直接计算实现时的问题。幸运的是, NVIDIA 开发了一个光线跟踪库,名为 NVIDIA OptiX ,它使用 GPU 并行性来实现显著的加速。在 Blender Python 环境中使用 NVIDIA OptiX 将带来实实在在的好处。
概括
这篇文章描述了两种不同的加速矩阵乘法的方法。第一种方法使用 Numba 编译器来减少 Python 代码中与循环相关的开销。第二种方法使用 CUDA 并行化矩阵乘法。速度比较证明了 CUDA 在加速矩阵乘法方面的有效性。
因为前面描述的 CUDA 加速代码可以作为 Blender Python 脚本运行,所以可以在 Blender Python 环境中使用 CUDA 加速任意数量的算法。这大大提高了 blenderpython 作为科学计算工具的有效性。
关于作者
Eric Leonard 博士获得了博士学位。在马里兰大学机械工程系,他专门从事理论和计算流体力学。研究生毕业后,他在马萨诸塞州剑桥市的三菱 Ele CTR ic 研究实验室实习,致力于开发一种替代传统计算流体力学算法的方法。在 Rendered 。 AI ,他使用 CUDA 加速了合成孔径雷达仿真代码库。
Nathan Kundtz 博士是物理学家、工程师和企业家。他与建筑公司、杜克大学以及众多其他组织合作,寻找并建立大公司。 Kundtz 博士拥有电子工程硕士学位和博士学位。来自杜克大学物理系。他的工作涵盖了人工智能、超材料、微波器件和低温凝聚态物理。著有或合著专利及专利申请 40 余项,同行评议出版物 30 余篇;包括获奖的博士研究。 Kundtz 博士被 LinkedIn 评为 40 岁以下十大科技专业人士之一。他是高盛 100 位最具吸引力的企业家之一, 40 岁以下的 Puget Sound ,并入选杜克大学研究生院为数不多的 Glasson 社团。
Ethan Sharratt 是 Rendered.AI 的软件工程总监。他有一个学士学位,在华盛顿大学的 EDE CTR 工程,目前正在一个硕士。他拥有 10 年在具有挑战性的环境中构建软件和固件解决方案的经验,包括开发空间等级软件定义的无线电、信号和图像处理以及实时计算机视觉管道。
Steven Forsyth 是 NVIDIA 的解决方案架构师,专注于支持联邦生态系统。他在激光干涉仪引力波天文台工作了几年,在那里他获得了信号处理和高性能计算方面的经验。在 NVIDIA ,他将从 LIGO 获得的知识与深度学习的知识结合起来,专门从事深度学习应用,涉及广泛的领域,包括计算机视觉和网络安全。史蒂文最近从乔治亚理工学院毕业,在那里他获得了物理学学士学位。
审核编辑:郭婷
-
NVIDIA
+关注
关注
14文章
5104浏览量
104370 -
CUDA
+关注
关注
0文章
122浏览量
13784
发布评论请先 登录
相关推荐
Mali GPU编程特性及二维浮点矩阵运算并行优化详解

请问Mali GPU的并行化计算模型是怎样构建的?
【KV260视觉入门套件试用体验】硬件加速之—使用PL加速矩阵乘法运算(Vitis HLS)
基于Spark的矩阵分解并行化算法
基于深度学习的矩阵乘法加速器设计方案
面向数组计算任务而设计的Numba具有CUDA加速功能
一行Python代码如何实现并行化
使用map函数实现Python程序并行化
如何在OpenCV中实现CUDA加速
CUDA矩阵乘法优化手段详解
CUDA与Jetson Nano:并行Pollard Rho测试





 使用CUDA并行化矩阵乘法加速Blender Python
使用CUDA并行化矩阵乘法加速Blender Python










评论