详解频谱分析仪的基本原理

本文的目的是为您提供关于频谱仪或信号分析仪的基本概述。您或许想要进一步了解与频谱分析相关的更多其他话题，您可访问频谱分析仪网页。这里将重点介绍频谱分析仪工作的基本原理。虽然今天的技术使得现代数字实现替代许多模拟电路成为可能，但是从经典的频谱分析仪结构开始了解仍然非常有好处。今后我们还将探讨数字电路赋予频谱仪的功能及优势，以及讨论现代频谱仪中所使用的数字架构。

图 2-1 是一个超外差频谱仪的简化框图。“外差”是指混频，即对频率进行转换，而“超”则是指超音频频率或高于音频的频率范围。从图中我们看到，输入信号先经过一个衰减器，再经低通滤波器(稍后会看到为何在此处放置滤波器)到达混频器，然后与来自本振(LO)的信号相混频。

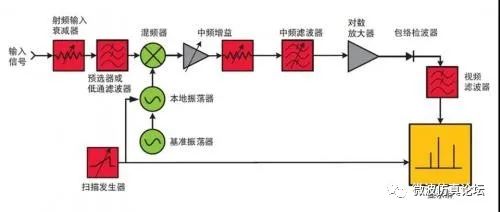
图 2-1. 典型超外差频谱分析仪的结构框图

由于混频器是非线性器件，其输出除了包含两个原始信号之外，还包含它们的谐波以及原始信号与其谐波的和信号与差信号。若任何一个混频信号落在中频(IF)滤波器的通带内，它都会被进一步处理(被放大并可能按对数压缩)。基本的处理过程有包络检波、低通滤波器进行滤波以及显示。斜波发生器在屏幕上产生从左到右的水平移动，同时它还对本振进行调谐，使本振频率的变化与斜波电压成正比。

如果您熟悉接收普通调幅(AM)广播信号的超外差调幅收音机，您一定会发现它的结构与图 2-1 所示框图极为相似。差别在于频谱分析仪的输出是屏幕而不是扬声器，且其本振调谐是电子调谐而不是靠前面板旋钮调谐。

既然频谱分析仪的输出是屏幕上的 X-Y 迹线，那么让我们来看看从中能获得什么信息。显示被映射在由 10 个水平网格和 10 个垂直网格组成的标度盘上。横轴表示频率，其标度值从左到右线性增加。频率设置通常分为两步：先通过中心频率控制将频率调节到标度盘的中心线上，然后通过频率扫宽控制再调节横跨 10 个网格的频率范围(扫宽)。这两个控制是相互独立的，所以改变中心频率时，扫宽并不改变。还有，我们可以采用设置起始频率和终止频率的方式来代替设置中心频率和扫宽的方式。不管是哪种情况，我们都能确定任意被显示信号的绝对频率和任何两个信号之间的相对频率差。

纵轴标度按幅度大小划分。可以选用以电压定标的线性标度或以分贝(dB)定标的对数标度。对数标度比线性标度更经常使用，因为它能反映出更大的数值范围。对数标度能同时显示幅度相差 70 至 100 dB(电压比为 3200 至 100,000 或功率比为 10,000,000 至 10,000,000,000)的信号，而线性标度则只能用于幅度差不大于 20 至 30 dB(电压比 10 至 32)的信号。在这两种情况下，我们都会运用校准技术1给出标度盘上最高一行的电平即基准电平的绝对值，并根据每个小格所对应的比例来确定标度盘上其他位置的值。这样，我们既能测量信号的绝对值，也能测量任意两个信号的相对幅度差。

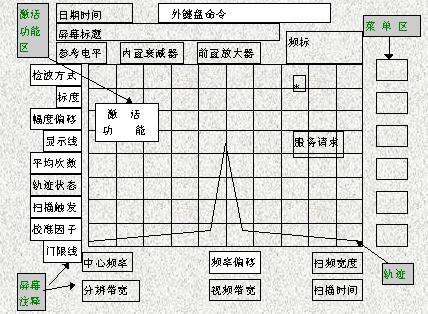
屏幕上会注释出频率和幅度的标度值。图 2-2 是一个典型的频谱分析仪的显示。

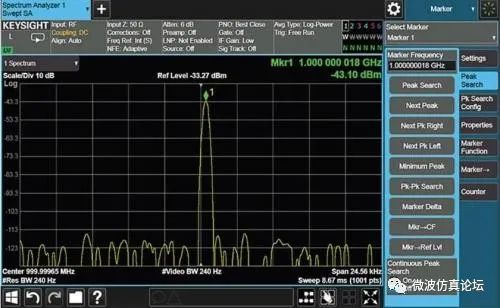
图 2-2. 参数已设定的典型频谱分析仪显示图

现在让我们将注意力再回到图 2-1 中所显示的频谱分析仪元器件。

射频衰减器

分析仪的第一部分是射频衰减器。它的作用是保证信号在输入混频器时处在合适的电平上，从而防止发生过载、增益压缩和失真。由于衰减器是频谱仪的一种保护电路，所以它通常是基于基准电平值而自动设置，不过也能以 10 dB、5 dB、2 dB 甚至 1 dB 的步进来手动选择衰减值。图 2-3 所示是一个以 2 dB 为步进量、最大衰减值为 70 dB 的衰减器电路的例子。

其中隔直电容是用来防止分析仪因直流信号或信号的直流偏置而被损坏，不过它会对低频信号产生衰减，并使一些频谱仪的最低可用起始频率增加至 9 kHz、100 kHz 或 10 MHz。

在有些分析仪中，可以像图 2-3 那样连接一个幅度基准信号，它提供了一个有精确频率和幅度的信号，用于分析仪周期性的自我校准。

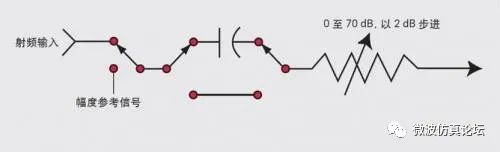
图 2-3. 射频衰减器电路

低通滤波器或预选器

低通滤波器的作用是阻止高频信号到达混频器。从而可以防止带外信号与本振相混频，在中频上产生多余的频率响应。微波频谱分析仪或信号分析仪用预选器代替了低通滤波器，预选器是一种可调滤波器，能够滤掉我们所关心的频率以外的其他频率上的信号。在第 7 章里，我们将详细介绍对输入信号进行过滤的目的和方法。

分析仪调谐

我们需要知道怎样将频谱分析仪或信号分析仪调谐至我们所希望的频率范围。调谐取决于中频滤波器的中心频率、本振的频率范围和允许外界信号到达混频器(允许通过低通滤波器)的频率范围。从混频器输出的所有信号分量中，有两个具有最大幅度的信号是我们最想得到的，它们是由本振与输入信号之和以及本振与输入信号之差所产生的信号分量。如果我们能使想观察的信号比本振频率高或低一个中频，则所希望的混频分量之一就会落入中频滤波器的通带之内，随后会被检波并在屏幕上产生幅度响应。

为了使分析仪调谐至所需的频谱范围，我们需要选择合适的本振频率和中频。假定要求的调谐范围是 0 至 3.6 GHz，接下来需要选择中频频率。如果选择 1 GHz 的中频，这个频率处在所需的调谐范围内，我们可以得到一个 1 GHz 的输入信号，又由于混频器的输出包含原始输入信号，那么来自于混频器的 1 GHz 输入信号将在中频处有恒定的输出。所以不管本振如何调谐，1 GHz 的信号都将通过系统，并在屏幕上给出恒定的幅度响应。其结果是在频率调谐范围内形成一个无法进行测量的空白区域，因为在这一区域的信号幅度响应独立于本振频率。所以不能选择 1 GHz 的中频。

也就是说，我们应在比调谐频段更高的频率上选择中频。在可调谐至 3.6 GHz 的 Keysight X 系列信号分析仪中，第一个本振频率范围为 3.8 至 8.7 GHz，选择的中频频率约为 5.1 GHz。

现在我们想从 0 Hz(由于这种结构的仪器不能观察到 0 Hz 信号，故实际上是从某个低频)调谐到 3.6 GHz。

选择本振频率从中频开始(LO - IF = 0 Hz)并向上调谐至高于中频 3.6 GHz，则 LO - IF 的混频分量就能够覆盖所要求的调谐范围。运用这个原理，可以建立如下调谐方程：

如果想要确定分析仪调谐到低频、中频或高频信号(比如 1 kHz、1.5 GHz 或 3 GHz)所需的本振频率，首先要变换调谐方程得到 fLO:

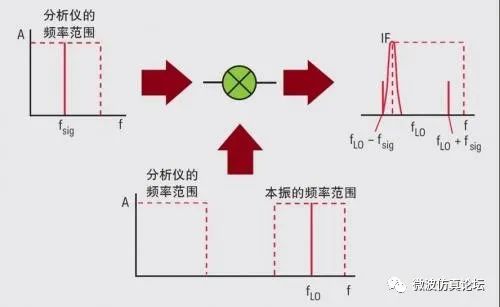
图 2-4. 为了在显示屏上产生响应，本振必须调谐到 fIF + fs

图 2-4 举例说明了分析仪的调谐过程。图中，fLO 并未高到使 fLO -fsig 混频分量落入 IF 通带内，故在显示器上没有响应。但是，如果调整斜波发生器使本振调谐到更高频率，则混频分量在斜波(扫描)的某点上将落入 IF 通带内，我们将看到显示器上出现响应。

由于斜波发生器能同时控制显示器上迹线的水平位置和本振频率，因此可以根据输入信号的频率来校准显示器的横轴。

我们还未完全解决调谐问题。如果输入信号频率是 9.0 GHz，会发生什么情况呢?当本振调谐在 3.8 至 8.7 GHz 的范围时，在它到达远离 9.0 GHz 输入信号的中频(3.9 GHz)时，会得到一个频率与中频频率相等的混频分量，并在显示器上生成响应。换句话说，调谐方程很容易地成为：

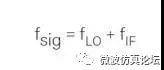
这个公式表明图 2-1 的结构也能得到 8.9 至 13.8 GHz 的调谐范围，但前提是允许此范围内的信号到达混频器。

图 2-1 中输入端低通滤波器的作用就是阻止这些高频信号到达混频器。如前所述，我们还要求中频信号本身不会到达混频器，那么低通滤波器必须能对 5.1 GHz 以及 8.9 至 13.8 GHz 范围内的信号进行有效的衰减。

总之，可以认为对于单频段射频频谱分析仪，选择的中频频率应高于调谐范围的最高频率，使本振可以从中频调谐至调谐范围的上限频率加上中频，同时在混频器前端放置低通滤波器来滤除 IF 以下的频率。

为了分辨频率上非常接近的信号(见稍后的“信号分辨”一节)，有些频谱仪的中频带宽窄至 1 kHz，有些达到 10 Hz 甚至 1 Hz。这样的窄带滤波器很难在 5.1 GHz 的中心频率上实现，因此必须增加另外的混频级(一般为 2 至 4 级)来把第一中频下变频到最后的中频。图 2-5 是一种基于典型频谱分析仪结构的中频变换链。

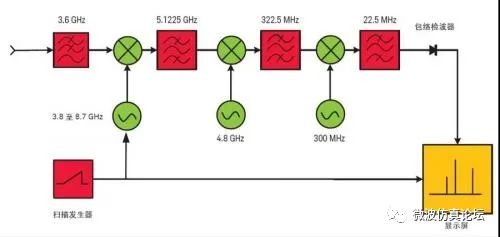
图 2-5. 大多数频谱分析仪使用 2 至 4 个混频步骤以达到最后的中频。

对应的完整的调谐方程为：

可以看出它与仅仅使用第一个中频的简化调谐方程得到一样的结果。虽然图 2-5 中只画出了无源滤波器，但实际还有更窄中频级的放大。基于频谱仪自身的设计，最终的中频结构可能还包括对数放大器或模数转换器等其他器件。

大多数射频频谱分析仪都允许本振频率和第一中频一样低，甚至更低。由于本振和混频器的中频端口之间的隔离度有限，故本振信号也会出现在混频器输出端。当本振频率等于中频时，本振信号自身也被系统处理并在显示器上出现响应，就像输入了一个 0 Hz 的信号一样。这种响应称为本振馈通，它会掩盖低频信号。所以并不是所有的频谱仪的显示范围都能包含 0 Hz。

中频增益

再看图 2-1，结构框图的下一个部分是一个可变增益放大器。它用来调节信号在显示器上的垂直位置而不会影响信号在混频器输入端的电平。当中频增益改变时，基准电平值会相应的变化以保持所显示信号指示值的正确性。通常，我们希望在调节输入衰减时基准电平保持不变，所以射频衰减器和中频增益的设置是联动的。

在输入衰减改变时，中频增益会自动调整来抵消输入衰减变化所产生的影响，从而使信号在显示器上的位置保持不变。

信号分辨

中频增益放大器之后，就是由模拟和/或数字分辨率带宽(RBW)滤波器组成的中频部分。

模拟滤波器

频率分辨率是频谱分析仪或信号分析仪明确分离出两个正弦输入信号响应的能力。傅立叶理论告诉我们正弦信号只在单点频率处有能量，好像我们不应该有什么分辨率问题。两个信号无论在频率上多么接近，似乎都应在显示器上表现为两条线。但是超外差接收机的显示器上所呈现的信号响应是具有一定宽度的。

混频器的输出包括两个原始信号(输入信号和本振)以及它们的和与差。中频由带通滤波器决定，此带通滤波器会选出所需的混频分量并抑制所有其他信号。由于输入信号是固定的，而本振是扫频的，故混频器的输出也是扫频的。若某个混频分量恰好扫过中频，就会在显示器上将带通滤波器的特性曲线描绘出来，如图 2-6 所示。链路中最窄的滤波器带宽决定了总显示带宽。在图 2-5 所示结构中，该滤波器具有 22.5 MHz的中频。

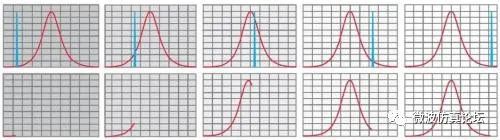
图 2-6. 当混频分量扫过 IF 滤波器时，显示器上描绘出滤波器的特性曲线。

因此，两个输入信号频率必须间隔足够远，否则它们所形成的迹线会在顶部重叠，看起来像是只有一个响应。所幸的是，频谱分析仪中的分辨率(IF)滤波器可调，所以通常能找到一个带宽足够窄的滤波器来分离频率间隔很近的信号。

是德科技频谱分析仪或信号分析仪的技术资料列出了可用的 IF 滤波器的 3 dB 带宽，以便描述频谱仪分辨信号的能力。这些数据告诉我们两个等幅正弦波相距多近时还能依然被分辨。这时由信号产生的两个响应曲线的峰值处有 3 dB 的凹陷，如图 2-7 所示，两个信号可以被分辨。当然这两个信号还可以再近一些直到它们的迹线完全重叠，但通常以 3 dB 带宽作为分辨两个等幅信号的经验值。

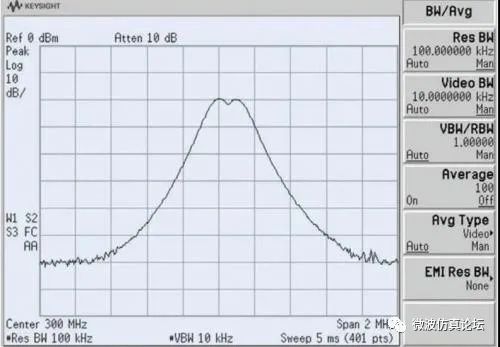
图 2-7. 能够分辨出间距等于所选 IF 滤波器 3 dB 带宽的两个等幅正弦信号。

如果采用标准(正态)检波模式(见本章后面的“检波类型”)，需要使用足够的视频滤波平滑信号迹线，否则因两个信号相互作用就会有拖尾现象。虽然拖尾的迹线指出了存在不止一个信号，但是很难测定每路信号的幅度。默认检波模式是正峰值检波的频谱仪显示不出拖尾效应，可以通过选择取样检波模式来进行观察。

我们碰到更多的情况是不等幅正弦波。有可能较小的正弦波被较大信号响应曲线的边带所淹没。这种现象如图 2-8 所示。顶部的迹线看起来是一个信号，但实际上它包含两个：一个频率为 300 MHz(0 dBm)，另一个频率为 300.005 MHz(-30 dBm)。在去除 300 MHz 的信号后，较小的信号才会显示出来。

分辨率滤波器的另一个技术指标是带宽选择性(也称选择性或形状因子)。带宽选择性决定了频谱仪分辨不等幅正弦信号的能力。是德科技频谱分析仪的带宽选择性通常指定为 60 dB 带宽与 3 dB 带宽之比，如图 2-9 所示。是德科技分析仪中的模拟滤波器具有 4 个极点，采用同频调谐式设计，其特性曲线形状类似高斯分布4。这种滤波器的带宽选择性约为 12.7:1。

那么，假定带宽选择性是 12.7:1，若要分辨频率相差 4 kHz、幅度相差 30 dB 的两个信号，应如何选择分辨率带宽呢?

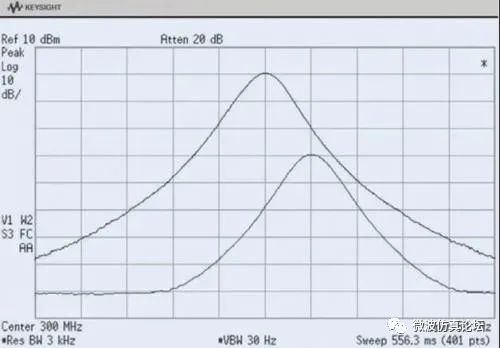
图 2-8. 低电平信号被淹没在较大信号响应曲线的边带里

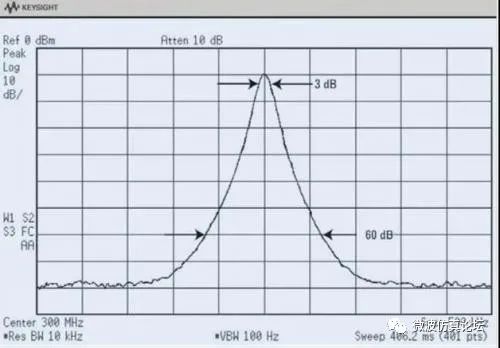
图 2-9. 带宽选择性：60 dB 带宽与 3 dB 带宽之比

一些老式频谱分析仪或信号分析仪对于最窄的分辨带宽滤波器采用 5 个极点从而改善带宽选择性至 10:1。新型分析仪通过使用数字 IF 滤波器可以达到更好的带宽选择性。

由于我们关心的是当分析仪调谐至较小信号时对较大信号的抑制情况，因此不需要考虑整个带宽，而只需考虑从滤波器中心频率到边缘的频率范围。为确定在给定频偏时滤波器边带下降了多少，使用如下方程：

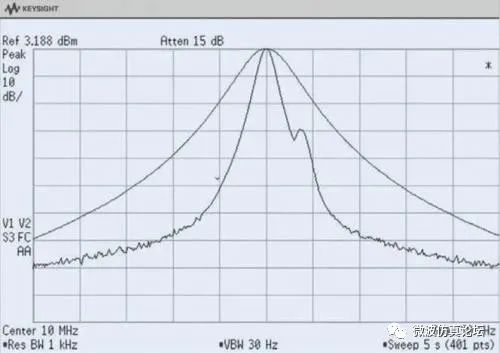
图 2-10. 带宽为 3 kHz(上方迹线)不能分辨出较小信号，带宽减小到 1 kHz(下方迹线)时则能分辨

数字滤波器

一些频谱分析仪使用数字技术实现分辨率带宽滤波器。数字滤波器有很多优点，例如它能极大地改善滤波器的带宽选择性。是德科技公司的 PSA 系列和 X 系列分析仪实现了分辨率带宽滤波器的全部数字化。另外像 Keysight ESA-E 系列频谱仪，采用的是混合结构：带宽较大时采用模拟滤波器，带宽小于等于 300 Hz 时采用数字滤波器。

剩余 FM

最小可用分辨率带宽通常由分析仪中本振(尤其是第一本振)的稳定度和剩余调频决定。早期的频谱仪设计使用不稳定的 YIG (钇铁石榴石)振荡器，通常具有大约 1 kHz 的残余调频。由于这种不稳定性被传递给与本振相关的混频分量，再将分辨率带宽减小至1KHz以下是没有意义的，因为不可能确定这种不稳定性的准确来源。

不过，现代分析仪已经极大的改善了残余调频。比如是德科技高性能 X 系列信号分析仪具有 0.25 Hz(标称值)的剩余调频;PSA 系列频谱分析仪为 1 至 4 Hz;ESA 系列频谱仪为 2 至 8 Hz。这使得分辨率带宽可以减小至 1 Hz。因此，分析仪上出现的任何不稳定性都是由输入信号造成的。

相位噪声

没有一种振荡器是绝对稳定的。虽然我们看不到频谱分析仪本振系统的实际频率抖动，但仍能观察到本振频率或相位不稳定性的明显表征，这就是相位噪声(有时也叫噪声边带)。

它们都在某种程度上受到随机噪声的频率或相位调制的影响。如前所述，本振的任何不稳定性都会传递给由本振和输入信号所形成的混频分量，因此本振相位噪声的调制边带会出现在幅度远大于系统宽带底噪的那些频谱分量周围(图 2-11)。显示的频谱分量和相位噪声之间的幅度差随本振稳定度而变化，本振越稳定，相位噪声越小。它也随分辨率带宽而变，若将分辨率带宽缩小 10 倍，显示相位噪声电平将减小 10 dB5。

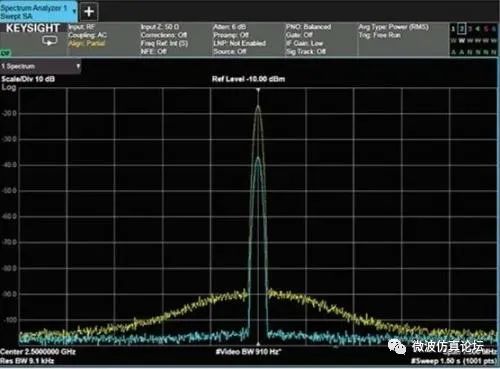
图 2-11.只有当信号电平远大于系统底噪时，才会显示出相位噪声

相位噪声频谱的形状与分析仪的设计，尤其是用来稳定本振的锁相环结构有关。在某些分析仪中，相位噪声在稳定环路的带宽中相对平坦，而在另一些分析仪中，相位噪声会随着信号的频偏而下降。相位噪声采用 dBc(相对于载波的 dB 数)为单位，并归一化至 1 Hz 噪声功率带宽。有时在特定的频偏上指定，或者用一条曲线来表示一个频偏范围内的相位噪声特性。

通常，我们只能在分辨率带宽较窄时观察到频谱仪的相位噪声，此时相位噪声使这些滤波器的响应曲线边缘变得模糊。使用前面介绍过的数字滤波器也不能改变这种效果。对于分辨率带宽较宽的滤波器，相位噪声被掩埋在滤波器响应曲线的边带之下，正如之前讨论过的两个非等幅正弦波的情况。

一些现代频谱分析仪或信号分析仪允许用户选择不同的本振稳定度模式，使得在各种不同的测量环境下都能具备最佳的相位噪声。例如，高性能 X 系列信号分析仪提供 3 种模式：

– 距载波频偏小于 140 kHz 时的相位噪声优化。在此模式下，载波附近的本振相位噪声被优化，而 140 kHz 之外的相位噪声不具备最优特性。

– 距载波频偏大于 160 kHz 时的相位噪声优化。这种模式优化距载波频偏大于 160 KHz 处的相位噪声。

– 优化本振用于快速调谐。当选择这种模式，本振的特性将折衷所有距载波频偏小于 2 MHz 范围内的相位噪声。这样在改变中心频率或扫宽时允许在最短的测量时间内保证最大的测量吞吐量。

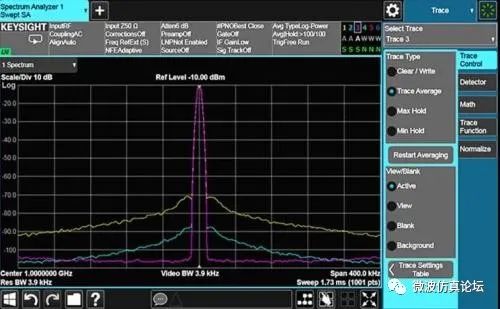
图 2-12a. 相位噪声性能在不同测量环境下的优化

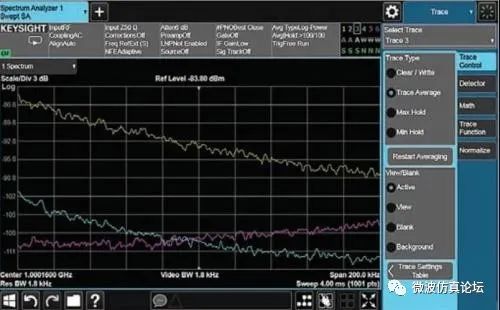
图 2-12b. 距载波频偏为 140 kHz 处的详细显示

高性能 X 系列信号分析仪的相位噪声优化还可以设为自动模式，这时频谱仪会根据不同的测量环境来设置仪器，使其具有最佳的速度和动态范围。当扫宽 > 44.44 MHz 或分辨率带宽 > 1.9 MHz 时，分析仪选择快速调谐模式。另外，当中心频率< 195 kHz 或当中心频率 ≥ 1 MHz 且扫宽 ≤ 1.3 MHz、分辨率带宽 ≤ 75 kHz 时，分析仪自动选择最佳近端载波相位噪声。在其他情况下，分析仪会自动选择远端最佳相位噪声。

在任何情况下，相位噪声都是频谱分析仪或信号分析仪分辨不等幅信号能力的最终限制因素。如图 2-13所示，根据 3 dB 带宽和选择性理论，我们应该能够分辨出这两个信号，但结果是相位噪声掩盖了较小的信号。

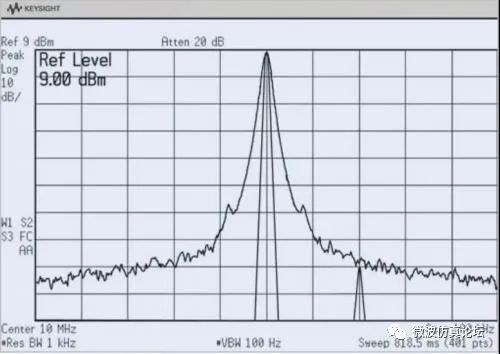
图 2-13. 相位噪声阻碍了对非等幅信号的分辨

扫描时间

模拟分辨率滤波器

如果把分辨率作为评价频谱仪的唯一标准，似乎将频谱仪的分辨率(IF)滤波器设计得尽可能窄就可以了。然而，分辨率会影响扫描时间，而我们又非常注重扫描时间。因为它直接影响完成一次测量所需的时间。

考虑分辨率的原因是由于中频滤波器是带限电路，需要有限的时间来充电和放电。如果混频分量扫过滤波器的速度过快，便会造成如图 2-14 所示的显示幅度的丢失。(关于处理中频响应时间的其他方法，见本章后面所述的“包络检波器”。)如果我们考虑混频分量停留在中频滤波器通带内的时间，则这个时间与带宽成正比，与单位时间内的扫描(Hz)成反比，即：

通带内的时间 =

许多模拟分析仪中所采用的同步调谐式准高斯滤波器的 k 值在 2 至 3 之间。

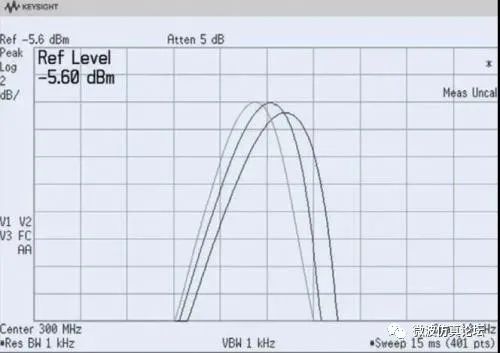
图 2-14. 扫描过快引起显示幅度的下降和所指定频率的偏移

我们得出的重要结论是：分辨率的变化对扫描时间有重大影响。老式模拟分析仪通常都能按 1、3、10 的规律或大致等于 10 的平方根的比率提供步进值。所以，当分辨率每改变一档，扫描时间会受到约 10 倍的影响。Keysight X 系列信号分析仪提供的带宽步进可达 10%，以实现扫宽、分辨率和扫描时间三者更好的折衷。

频谱分析仪一般会根据扫宽和分辨率带宽的设置自动调整扫描时间，通过调节扫描时间来维持一个被校准的显示。必要时，我们可以不使用自动调节而采用手动方式设定扫描时间。如果所要求的扫描时间比提供的最大可用扫描时间还短，频谱仪会在网格线右上方显示“Meas Uncal”以表示显示结果未经校准。

数字分辨率滤波器

是德科技频谱分析仪或信号分析仪中所使用的数字分辨率滤波器对扫描时间的影响与之前所述的模拟滤波器不同。对于扫描分析，利用数字技术实现的滤波器在不进行更深入处理的条件下，扫描速度提高至原来的 2 至 4倍。

而配有选件 FS1 的 X 系列信号分析仪利用编程方法可以校正分辨率带宽在大约 3 kHz 至 100 kHz 之间时扫描速度过快的影响。因此取决于特定的设置，扫描时间可以从秒级缩短到毫秒级。见图 2-14a。不包括校正过程的扫描时间将达到 79.8 秒。图 2-14b 显示了分析仪配有选件 FS1 时，扫描时间达 1.506 秒。对于这些最宽的分辨率带宽，扫描时间已经非常短。例如，在 k = 2、1 GHz 扫宽、1 MHz 分辨率带宽条件下，使用公式计算得出扫描时间仅为 2 毫秒。

对于较窄的分辨率带宽，Keysight 频谱分析仪或信号分析仪使用快速傅立叶变换(FFT)来处理数据，因此扫描时间也会比公式预计的时间短。由于被分析的信号是在多个频率范围中进行处理，所以不同的分析仪会有不同的性能表现。例如，如果频率范围为 1 kHz，那么当我们选择 10 Hz 的分辨率带宽时，分析仪实际上是在 1 kHz 单元中通过 100 个相邻的 10 Hz 滤波器同时处理数据。如果数字处理的速度能达到瞬时，那么可以预期扫描时间将缩短 100 倍。实际上缩减的程度要小些，但仍然非常有意义。

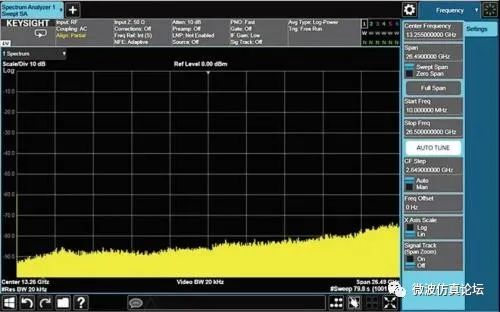
图 2-14a. 20 kHz RBW、未配有选件 FS1 时的全扫宽扫描速度

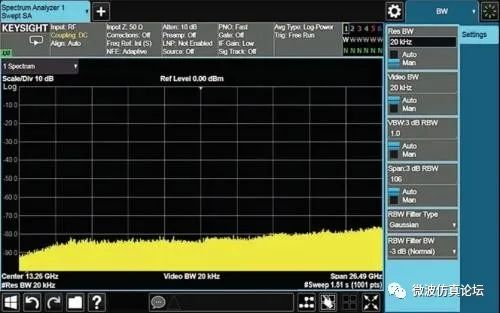
图 2-14b. 20 kHz RBW、配有选件 FS1 时的全扫宽扫描速度

包络检波器

老式分析仪通常会使用包络检波器将中频信号转换为视频信号7。最简单的包络检波器由二极管、负载电阻和低通滤波器组成，如图 2-15 所示。示例中的中频链路输出信号(一个幅度调制的正弦波)被送至检波器，检波器的输出响应随中频信号的包络而变化，而不是中频正弦波本身的瞬时值。

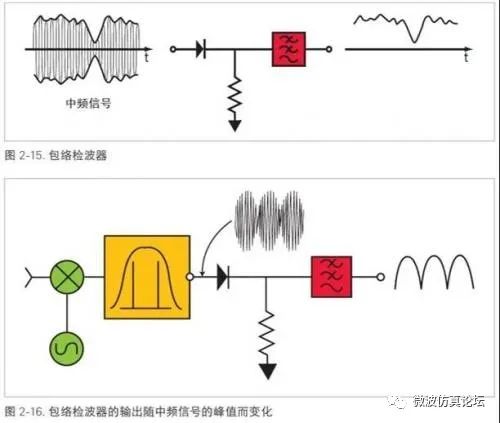
对大多数测量来说，我们选择足够窄的分辨率带宽来分辨输入信号的各个频谱分量。如果本振频率固定，频谱仪则调谐到信号的其中一个频谱分量上，那么中频输出就是一个恒定峰值的稳定正弦波。于是包络检波器的输出将是一个恒定(直流)电压，并没有需要检波器来跟踪的变化。

不过，有些时候我们会故意使分辨率带宽足够宽以包含两个或更多的频谱分量，而有些场合则别无选择，因为这些频谱分量之间的频率间隔比最窄的分辨率带宽还要小。假设通带内只含两个频谱分量，则两个正弦波会相互影响而形成拍音，如图 2-16 所示，中频信号的包络会随着两个正弦波间的相位变化而变化。

分辨率(中频)滤波器的带宽决定了中频信号包络变化的最大速率。该带宽决定了两个输入正弦波之间有多大的频率间隔从而在经混频后能够同时落在滤波器通带内。假设末级中频为 22.5 MHz，带宽为 100 kHz，那么两个间隔 100 kHz 的输入信号会产生 22.45 和 22.55 MHz 的混频分量，因而满足上述标准，如图 2-16 所示。检波器必须能够跟踪由这两个信号所引起的包络变化，而不是 22.5 MHz 中频信号本身的包络。

包络检波器使频谱分析仪成为一个电压表。让我们再次考虑上述中频通带内同时有两个等幅信号的情况，功率计所指示的电平值会比任何一个信号都要高 3 dB，也就是两个信号的总功率。假定两个信号靠得足够近，以致分析仪调谐至它们中间时由于滤波器的频响跌落而引起的衰减可以忽略不计。(对于这里所讨论的内容，我们假设滤波器具有理想的矩形特性。)

那么分析仪的显示将在任一信号电平 2 倍的电压值(大于 6 dB)与 0(在对数标度下为负无穷大)之间变化。记住这两个信号是不同频率的正弦信号(矢量)，所以它们彼此之间的相位也在不断变化，有时刚好同相，幅值相加，而有时又刚好反相，则幅值相减。

因此，包络检波器根据来自中频链路的信号峰值(而不是瞬时值)的变化而改变，导致信号相位的丢失，这将电压表的特性赋予了频谱分析仪。

数字技术实现的分辨率带宽滤波器不包括模拟的包络检波器，而是用数字处理计算出 I、Q 两路数据平方和的方根，这在数值上与包络检波器的输出相同。

一种频率范围从零(直流)到由电路元件决定的某个较高频率的信号。频谱仪早期的模拟显示技术用这种信号直接驱动 CRT 的垂直偏转，因此被称为视频信号。

显示

直到 20 世纪 70 年代中期，频谱分析仪的显示方式还是纯模拟的。显示的迹线呈现连续变化的信号包络，且没有信息丢失。但是模拟显示有着自身的缺点，主要的问题是处理窄分辨率带宽时所要求的扫描时间很长。在极端情况下，显示迹线会变成一个在阴极射线显像管(CRT)屏幕上缓慢移动的光点，而没有实际的迹线。所以，长扫描时间使显示变得没有意义。

是德科技(当时是惠普的一部分)率先提出了一种可变余辉存储的 CRT，能在它上面调节显示信息的消退速率。如果调节适当，那么在旧迹线刚刚消失的时刻新的迹线恰好出现以更新显示。这种显示是连续、无闪烁的，而且避免了迹线重叠带来的混淆。它的效果相当好，但是针对每个新的测量状态需要重新调整亮度和消退速度。

20 世纪 70 年代中期，数字电路发展起来，它很快被用于频谱分析仪中。一旦一条迹线被数字化并存入存储器后，便永久地用于显示。在不使图像变得模糊或变淡的前提下，以无闪烁的速率来刷新显示变得简单。在不使图像变得模糊或变淡的前提下，以无闪烁的速率来刷新显示变得简单。

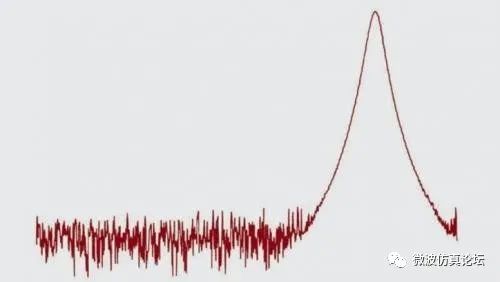
图 2-17. 对模拟信号进行数字化时，每个点应显示什么样的值?

检波器类型

采用数字显示，我们需要确定对每个显示数据点，应该用什么样的值来代表。无论我们在显示器上使用多少个数据点，每个数据点必须能代表某个频率范围或某段时间间隔(尽管在讨论频谱分析仪时通常并不会用时间)内出现的信号。

这个过程好似先将某个时间间隔的数据都放到一个信号收集单元(bucket)内，然后运用某一种必要的数学运算从这个信号收集单元中取出我们想要的信息比特。随后这些数据被放入存储器再被写到显示器上。这种方法提供了很大的灵活性。

这里我们将要讨论 6 种不同类型的检波器。

在图 2-18 中，每个信号收集单元内包含由以下公式决定的扫宽和时间帧的数据：

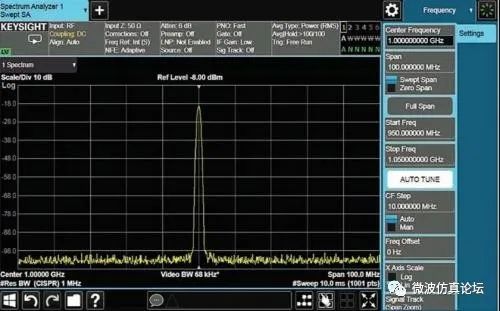
图 2-18. 1001 个迹线点(信号收集单元)中的每个点都覆盖了 100 kHz 的频率扫宽和 0.01 ms 的时间扫宽

频率：信号收集单元的宽度 = 扫宽/(迹线点数 – 1)

时间：信号收集单元的宽度 = 扫描时间/(迹线点数 – 1)

不同仪器的采样速率不同，但减小扫宽和/或增加扫描时间能够获得更高的精度，因为任何一种情况都会增加信号收集单元所含的样本数。采用数字中频滤波器的分析仪，采样速率和内插特性按照等效于连续时间处理来设计。

“信号收集单元”的概念很重要，它能够帮我们区分这 6 种显示检波器类型：

– 取样检波

– 正峰值检波(简称峰值检波)

– 负峰值检波

– 正态检波(Normal)

– 平均检波

– 准峰值检波

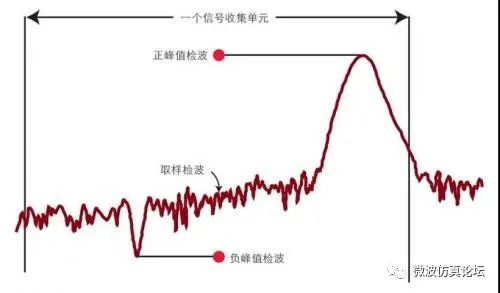
图 2-19. 存储器中存入的迹线点基于不同的检波器算法

前三种检波类型(取样、峰值和负峰值)比较容易理解，如图 2-19 中的直观表示。正态、平均和准峰值检波要复杂一些，我们稍后进行讨论。

我们回到之前的问题：如何用数字技术尽可能如实地显示模拟系统?我们来设想图 2-17 所描述的情况，即显示的信号只包含噪声和一个连续波(CW)信号。

取样检波

作为第一种方法，我们只选取每个信号收集单元的中间位置的瞬时电平值(如图 2-19)作为数据点，这就是取样检波模式。为使显示迹线看起来是连续的，我们设计了一种能描绘出各点之间矢量关系的系统。比较图 2-17 和 2-20，可以看出我们获得了一个还算合理的显示。当然，迹线上的点数越多，就越能真实地再现模拟信号。不同频谱仪的可用显示点数是不一样的，对于 X 系列信号分析仪，频域迹线的取样显示点数可以从最少 1 个点到最多 40001 个点。如图 2-21 所示，增加取样点确实可使结果更接近于模拟信号。

虽然这种取样检波方式能很好的体现噪声的随机性，但并不适合于分析正弦波。如果在高性能 X 系列信号分析仪上观察一个 100 MHz 的梳状信号，分析仪的扫宽可以被设置为 0 至 26.5 GHz即便使用 1001 个显示点，每个显示点代表 26.5 MHz 的频率扫宽(信号收集单元)，也远大于 8 MHz 的最大分辨率带宽。

结果，采用取样检波模式时，只有当梳状信号的混频分量刚好处在中频的中心处时，它的幅度才能被显示出来。图 2-22a 是一个使用取样检波的带宽为 750 Hz、扫宽为 10 MHz 的显示。它的梳状信号幅度应该与图 2-22b 所示(使用峰值检波)的实际信号基本一致。可以得出，取样检波方式并不适用于所有信号，也不能反映显示信号的真实峰值。当分辨率带宽小于采样间隔(如信号收集单元的宽度)时，取样检波模式会给出错误的结果。

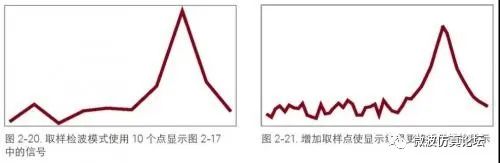
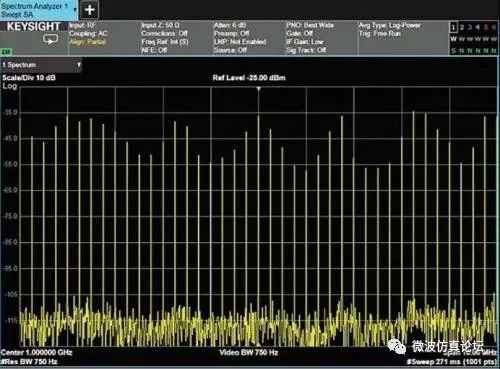
图 2-22a. 取样检波模式下的带宽为 250 kHz、扫宽为 10 MHz 的梳状信号

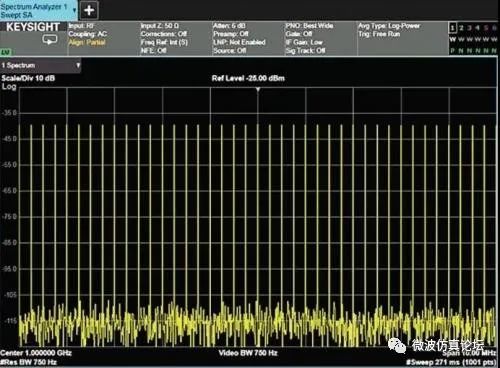
图 2-22b. 在 10 MHz 扫宽内，采用(正)峰值检波得到的实际梳状信号

(正)峰值检波

确保所有正弦波的真实幅度都能被记录的一种方法是显示每个信号收集单元内出现的最大值，这就是正峰值检波方式，或者叫峰值检波，如图 2-22b 所示。峰值检波是许多频谱分析仪默认的检波方式，因为无论分辨率带宽和信号收集单元的宽度之间的关系如何，它都能保证不丢失任何正弦信号。不过，与取样检波方式不同的是，由于峰值检波只显示每个信号收集单元内的最大值而忽略了实际的噪声随机性，所以在反映随机噪声方面并不理想。因此，将峰值检波作为第一检波方式的频谱仪一般还提供取样检波作为补充。

负峰值检波

负峰值检波方式显示的是每个信号收集单元中的最小值。大多数频谱仪都提供这种检波方式，尽管它不像其他方式那么常用。对于 EMC 测量，想要从脉冲信号中区分出 CW 信号，负峰值检波会很有用。在本应用指南后面的内容里，我们将看到负峰值检波还能应用于使用外部混频器进行高频测量时的信号识别。

正态检波

为了提供比峰值检波更好的对随机噪声的直观显示并避免取样检波模式显示信号的丢失问题，许多频谱仪还提供正态检波模式(俗称 rosenfell9 模式)。如果信号像用正峰值和负峰值检波所确定的那样既有上升、又有下降，则该算法将这种信号归类为噪声信号。

Roesnfell 并不是人名，而是一种运算方法的描述，用以测试在给定数据点代表的信号收集单元内的信号是上升还是下降，有时也写成 rose’n’fell。

在这种情况下，用奇数号的数据点来显示信号收集单元中的最大值，用偶数号的数据点来显示最小值。如图 2-25 所示。正态检波模式和取样检波模式在图 2-23a 和 2-13b中比较。(由于取样检波器在测量噪声时非常有效，所以它常被用于噪声游标应用。同样在信道功率测量和邻道功率测量中需要一种检波类型，可以提供无任何倾 向 的结果，此时适合使用峰值检波。对没有平均检波功能的频谱仪来说，取样检波是最好的选择。)

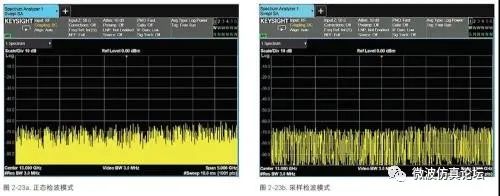
当遇到正弦信号时会是什么情况呢?我们知道，当混频分量经过中频滤波器时，频谱仪的显示器上会描绘出滤波器的特性曲线。如果滤波器的曲线覆盖了许多个显示点，便会出现下述情况：显示信号只在混频分量接近滤波器的中心频率时才上升，也只在混频分量远离滤波器中心频率时才下降。无论哪一种情况，正峰值和负峰值检波都能检测出单一方向上的幅度变化，并根据正态检波算法，显示每个信号收集单元内的最大值，如图 2-24 所示。

当分辨率带宽比信号收集单元窄时又会怎样呢?这时信号在信号收集单元内既有上升又有下降。如果信号收集单元恰好是奇数号，则一切正常，信号收集单元内的最大值将作为下一个数据点直接被绘出。但是，如果信号收集单元是偶数号的，那么描绘出的将是信号收集单元内的最小值。根据分辨率带宽和信号收集单元宽度的比值，最小值可能部分或完全不同于真实峰值(我们希望显示的值)。在信号收集单元宽度远大于分辨率带宽的极端情况下，信号收集单元内的最大值和最小值之差将是信号峰值和噪声之间的差值，图 2-25 的示例正是如此。观察第 6 个信号收集单元，当前信号收集单元中的峰值总是与前一个信号收集单元中的峰值相比较，当信号单元为奇数号时(如第 7 个单元)就显示两者中的较大值。此峰值实际上发生在第6 个信号收集单元，但在第 7 个单元才被显示出来。

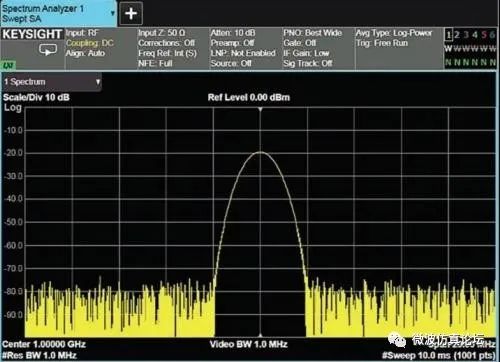
图 2-24. 当信号收集单元内的值只增大或只减小时，正态检波显示该单元内的最大值

正态检波算法：

如果信号值在一个信号收集单元内既有上升又有下降：则偶数号信号收集单元将显示该单元内的最小值(负峰值)。并记录最大值，然后在奇数号信号收集单元中将当前单元内的峰值与之前(记录的)一个单元的峰值进行比较并显示两者中的较大值(正峰值)。如果信号在一个信号收集单元内只上升或者只减小，则显示峰值，如图 2-25所示。

这个处理过程可能引起数据点的最大值显示过于偏向右方，但此偏移量通常只占扫宽的一个很小的百分数。一些频谱分析仪，例如高性能 X 系列信号分析仪，通过调节本振的起止频率来补偿这种潜在的影响。

另一种错误是显示峰值有两个而实际峰值只存在一个，图 2-26 显示出可能发生这种情况的例子。使用较宽分辨率带宽并采用峰值检波时两个峰值轮廓被显示出来。

因此峰值检波最适用于从噪声中定位 CW 信号，取样检波最适用于测量噪声，而既要观察信号又要观察噪声时采用正态检波最为合适。

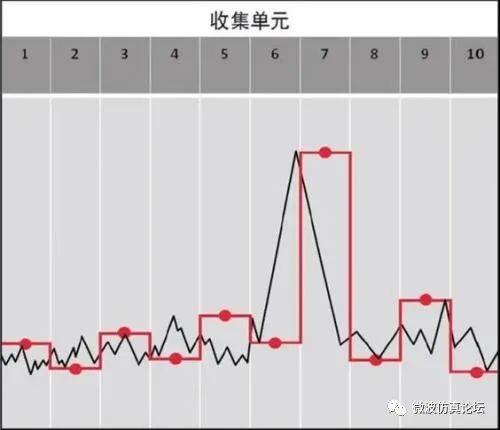
图 2-25. 正态检波算法所选择的显示迹线点

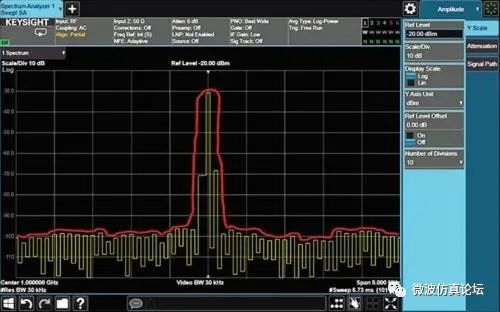
图 2-26. 正态检波显示出两个峰值而实际只存在一个

平均检波

虽然现代数字调制方案具有类噪声特性，但取样检波不能提供我们所需的所有信息。比如在测量一个 W-CDMA 信号的信道功率时，我们需要集成信号的均方根值，这个测量过程涉及到频谱仪一定频率范围内的信号收集单元的总功率，取样检波并不能提供这个信息。

虽然一般频谱仪是在每个信号收集单元内多次收集幅度数据，但取样检波只保留这些数据中的一个值而忽略其他值。而平均检波会使用该时间(和频率)间隔内的该信号收集单元内所有数据，一旦数据被数字化并且我们知道其实现的环境，便可以将数据以多种方法处理从而获得想要的结果。

某些频谱仪将功率(基于电压的均方根值)取平均的检波称为 rms(均方根) 检波。Keysight X 系列信号分析仪的平均检波功能包括功率平均、电压平均和信号的对数平均，不同的平均类型可以通过按键单独选择：

功率(rms)平均是对信号的均方根电平取平均值，这是将一个信号收集单元内所测得的电压值取平方和再开方然后除以频谱仪输入特性阻抗(通常为 50 Ω)而得到。功率平均计算出真实的平均功率，最适用于测量复杂信号的功率。

电压平均是将一个信号收集单元内测得的信号包络的线性电压值取平均。在 EMI 测试中通常用这种方法来测量窄带信号(这部分内容将在下一节做进一步讨论)。电压平均还可以用来观察 AM 信号或脉冲调制信号(如雷达信号、TDMA 发射信号)的上升和下降情况。

对数功率(视频)平均是将一个信号收集单元内所测得的信号包络的对数幅度值(单位为 dB)取平均。它最适合用来观察正弦信号，特别是那些靠近噪声的信号。

因此，使用功率为平均类型的平均检波方式提供的是基于 rms 电压值的真实平均功率，而平均类型为电压的检波器则可以看作是通用的平均检波器。平均类型为对数的检波器没有其他等效方式。

采用平均检波测量功率较取样检波有所改进。取样检波需要进行多次扫描以获取足够的数据点来提供精确的平均功率信息。平均检波使得对信道功率的测量从某范围内信号收集单元的求和变成代表着频谱仪某段频率的时间间隔的合成。在快速傅立叶变换(FFT)频谱仪12中，用于测量信道功率的值由显示数据点的和变为了 FFT 变换点之和。

在扫频和FFT两种模式下，这种合成捕获所有可用的功率信息，而不像取样检波那样只捕获取样点的功率信息。所以当测量时间相同时，平均检波的结果一致性更高。在扫描分析时也可以简单地通过延长扫描时间来提高测量结果的稳定性。

EMI 检波器：平均检波和准峰值检波

平均检波的一个重要应用是用于检测设备的电磁干扰(EMI)特性。在这种应用中，上一节所述的电压平均方式可以测量到可能被宽带脉冲噪声所掩盖的窄带信号。在 EMI 测试仪器中所使用的平均检波将取出待测的包络并使其通过一个带宽远小于 RBW 的低通滤波器，此滤波器对信号的高频分量(如噪声)做积分(取平均)运算。若要在一个没有电压平均检波功能的老式频谱分析仪中实现这种检波类型，需将频谱仪设置为线性模式并选择一个视频滤波器，它的截止频率需小于被测信号的最小 PRF(脉冲重复频率)。

准峰值检波(QPD)同样也用于 EMI 测试中。QPD 是峰值检波的一种加权形式，它的测量值随被测信号重复速率的下降而减小。也就是，一个给定峰值幅度并且脉冲重复速率为 10 Hz 的脉冲信号比另一个具有相同峰值幅度但脉冲重复速率为 1 kHz 的信号准峰值要低。这种信号加权是通过带有特定充放电结构的电路和由 CISPR 定义的显示时间常量来实现。

CISPR，国际无线电干扰特别委员会，由一些国际组织建立于 1934 年，致力于解决无线电干扰。它是由国际电工委员会(IEC)和许多其他国际组织的委员所组成的一个非政府组织,其所推荐的标准通常成为世界各地的政府监管机构所采用的法定 EMC 测试要求的基础。

QPD 也是定量测量信号“干扰因子”的一种方法。设想我们正在收听某一遭受干扰的无线电台，如果只是每隔几秒偶而听见由噪声所引起的“嗞嗞”声，那么基本上还可以正常收听节目，但是，如果相同幅度的干扰信号每秒出现 60 次，就无法再正常收听节目了。

平滑处理

在频谱仪中有几种不同的方法来平滑包络检波器输出幅度的变化。第一种方法是前面已经讨论过的平均检波，还有两种方法：视频滤波和迹线平均14。下面将对它们进行介绍。

视频滤波

要识别靠近噪声的信号并不只是 EMC 测量遇到的问题。如图 2-27 所示，频谱仪的显示是被测信号加上它自身的内部噪声。为了减小噪声对显示信号幅度的影响，我们常常对显示进行平滑或平均，如图 2-28 所示。频谱仪所包含的可变视频滤波器就是用作此目的。它是一个低通滤波器，位于包络检波器之后，并且决定了视频信号的带宽，该视频信号稍后将被数字化以生成幅度数据。此视频滤波器的截止频率可以减小到小于已选定的分辨率带宽(IF)滤波器的带宽。这时候，视频系统将无法再跟随经过中频链路的信号包络的快速变化。结果就是对被显示信号的平均或平滑。

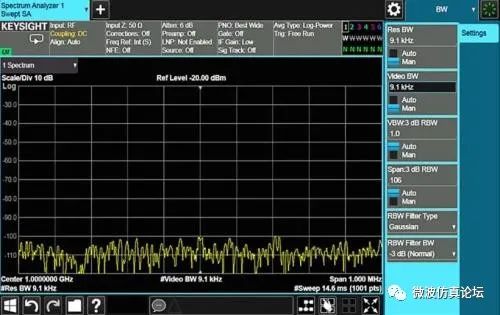
图 2-27. 频谱分析仪显示的信号加噪声

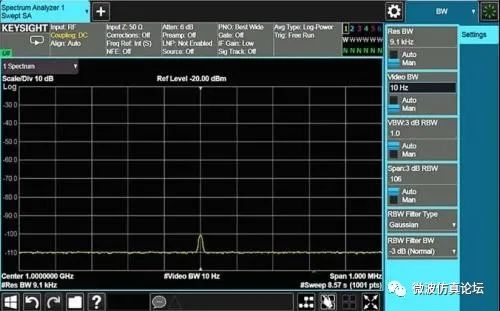
图 2-28. 图 2-27 中的信号经充分平滑后的显示

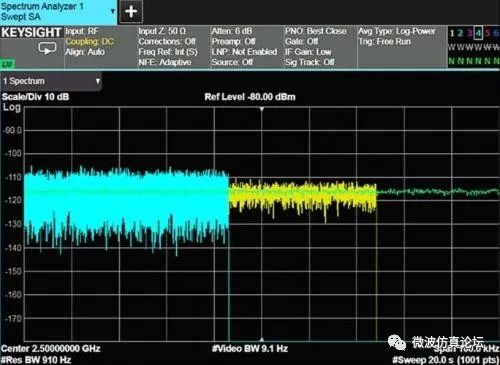
图 2-29. VBW 与 RBW 比值分别为 3:1、1:10、1:100 时的平滑效果

这种效果在测量噪声时最为明显，尤其是选用高分辨率带宽的时候。当减小视频带宽，那么噪声峰峰值的波动变化也随之减小。如图 2-29 所示，减小的程度(平均或平滑的程度)随视频带宽和分辨率带宽的比值而变。当比值小于或等于 0.01 时，平滑效果较好，而比值增大时，平滑效果则不太理想。视频滤波器不会对已经平滑的信号迹线(例如显示的正弦信号已可以很好地与噪声区分)有任何影响。

如果将频谱仪设置为正峰值检波模式，可以注意到以下两点：首先，如果 VBW > RBW，则改变分辨率带宽对噪声的峰峰值起伏影响不大。其次，如果 VBW < RBW，则改变视频带宽似乎会影响噪声电平。噪声起伏变化不大是因为频谱仪当前只显示了噪声的峰值。不过，噪声电平表现出随着视频带宽而变，这是由于平均(平滑)处理的变化，因而使被平滑的噪声包络的峰值改变，如图 2-30a。选择平均检波模式，平均噪声电平并不改变，如图 2-30b。

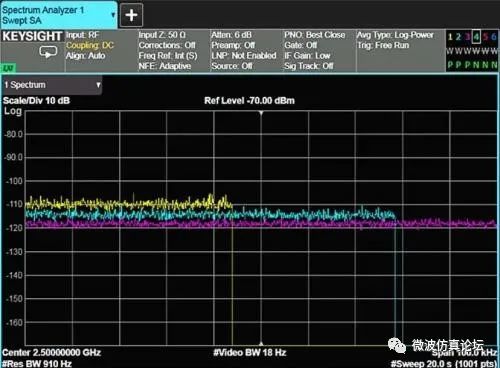
图 2-30a. 正峰值检波模式：减小视频带宽使峰值噪声变小，但不能降低平均噪声电平

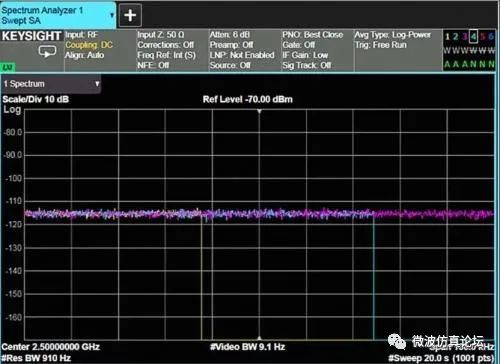
图 2-30b. 平均检波模式：无论 VBW 与 RBW 的比值为多少(3:1、1:10、1:100)，噪声电平保持不变

由于视频滤波器有自己的响应时间，因此当视频带宽 VBW 小于分辨率带宽 RBW 时，扫描时间的改变近似与视频带宽的变化成反比，扫描时间(ST)通过以下公式来描述：

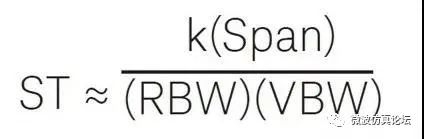
分析仪根据视频带宽、扫宽和分辨率带宽，自动设置相应的扫描时间。

迹线平均

数字显示提供了另一种平滑显示的选择：迹线平均。这是与使用平均检波器完全不同的处理过程。它通过逐点的两次或多次扫描来实现平均，每一个显示点的新数值由当前值与前一个平均值再求平均得到：

因此，经过若干扫描后显示会渐渐趋于一个平均值。通过设置发生平均的扫描次数，可以像视频滤波那样选择平均或平滑的程度。图 2-31 显示了不同扫描次数下获得的迹线平均效果。尽管迹线平均不影响扫描时间，但因为多次扫描需要一定的时间，因此要达得期望的平均效果所用的时间与采用视频滤波方式所用的时间大致相同。

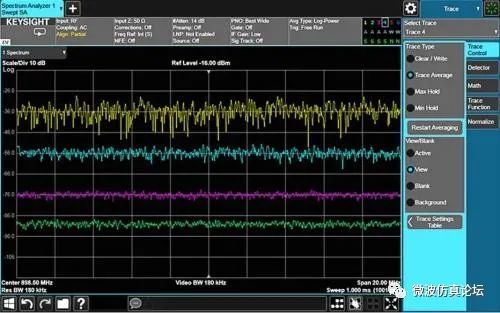
图 2-31. 扫描次数分别为 1、5、20、100(每组扫描对应迹线位置偏移从上到下)时的迹线平均效果

在大多数场合里无论选择哪种显示平滑方式都一样。如果被测信号是噪声或非常接近噪声的低电平正弦信号，则不管使用视频滤波还是迹线平均都会得到相同的效果。

不过，两者之间仍有一个明显的区别。视频滤波是对信号实时地进行平均，即随着扫描的进行我们看到的是屏幕上每个显示点的充分平均或平滑效果。每个点只做一次平均处理，在每次扫描上的处理时间约为 1/VBW。而迹线平均需要进行多次扫描来实现显示信号的充分平均，且每个点上的平均处理发生在多次扫描所需的整个时间周期内。

所以对于某些信号来说，采用不同的平滑方式会得到截然不同的效果。比如对一个频谱随时间变化的信号采用视频平均时，每次扫描都会得到不同的平均结果。但是如果选择迹线平均，所得到的结果将更接近于真实的平均值，见图 2-32a 和 2-32b。

图 2-32a 和 2-32b 显示对调频广播信号分别应用视频滤波和迹线平均，所产生的不同效果。

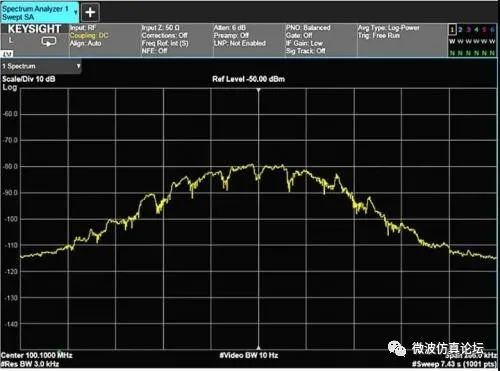
图 2-32a. 视频滤波

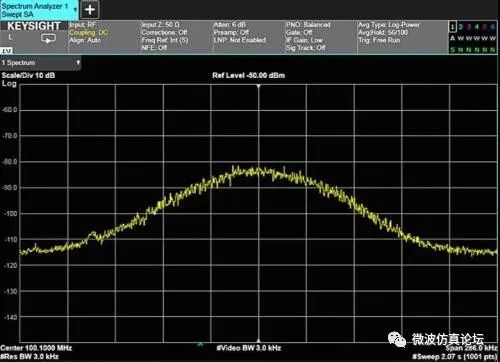
图 2-32b. 迹线平均

时间选通

具有时间选通功能的频谱分析仪可以获得频域上占据相同部分而时域上彼此分离的信号的频谱信息。通过利用外部触发信号调整这些信号间的间隔，可以实现如下功能：

– 测量在时域上彼此分离的多个信号中的任意一个(例如，您可以分离出两个时分而频率相同的无线信号的频谱)

– 测量 TDMA 系统中某个时隙的信号频谱

– 排除干扰信号的频谱，比如去除只存在于一段时间的周期性脉冲边缘的瞬态过程

为什么需要时间选通

传统的频域频谱分析仪在分析某些信号时只能提供有限的信息。这些较难分析的信号类型包括：

– 射频脉冲

– 时间复用

– 时分多址(TDMA)

– 频谱交织或非连续

– 脉冲调制

有些情况，时间选通功能可以帮助您完成一些往常即便有可能进行但也非常困难的测量。

测量时分双工信号

如何使用时间选通功能执行复杂的测量，请见图 2-33a。图中显示了一个简化的数字移动信号，其中包含无线信号 #1 和 #2，它们占据同一频道而时间分用。每路信号发送一个 1 ms 的脉冲，然后关闭，而后另一路信号再发送 1 ms。问题的关键是如何测量每个发射信号单独的频谱。

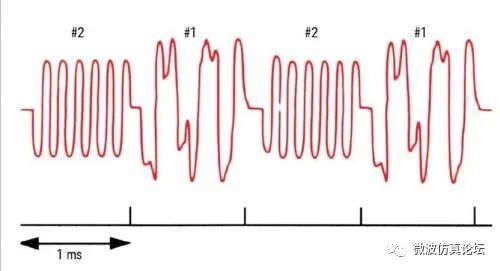
图 2-33a. 在时域里简化的数字移动无线信号

令人遗憾的是，传统的频谱分析仪并不能实现这一点。它只能显示两个信号的混合频谱，如图 2-33b 所示。而现代分析仪利用时间选通功能以及一个外部触发信号，就能够观察到单独的无线信号 #1(或 #2)的频谱并确定其是否存在所显示的杂散信号，如图2-33c。

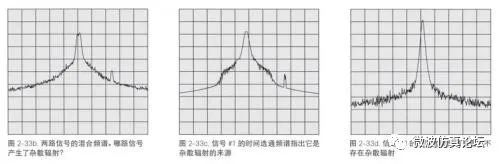
调整这些参数可以让您观察到所需的某个时间段的信号频谱。如果刚好在感兴趣的时间段里仅有一个选通信号，那么就可以使用如图 2-34 所示的电平选通信号。但是在许多情况下，选通信号的时间不会与我们要测量的频谱完全吻合。所以更灵活的方法是结合指定的选通时延和选通脉冲宽度采用边缘触发模式来精确定义想测量信号的时间周期。

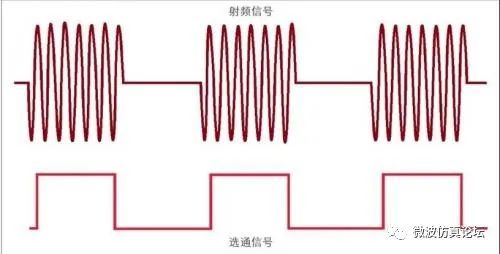
图 2-34. 电平触发：频谱分析仪只在选通触发信号高于某个确定的电平时才测量频谱

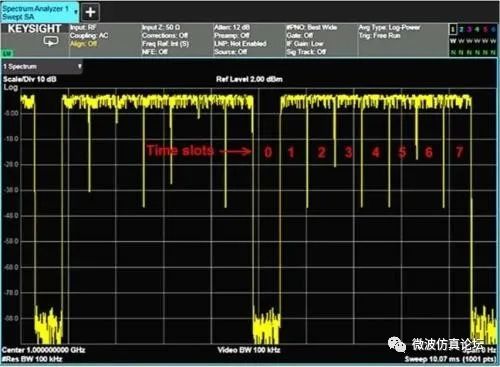
图 2-35. 采用 8 个时隙的 TDMA 信号(本例为 GSM 信号)，时隙 0 为“关闭”。

考虑如图 2-35 所示的 8 个时隙的 GSM 信号。每个突发脉冲序列的长度为 0.577 ms，整个帧长 4.615 ms。我们可能只对某个指定时隙内的信号频谱感兴趣。本例中假设 8 个可用时隙中使用了两个(时隙 1 和 3)，如图 2-36。当在频域中观察此信号时，见图 2-37，我们观察到频谱中存在多余的杂散信号。为了解决这个问题并找到干扰信号的来源，我们需要确定它出现在哪一个时隙里。如果要观察时隙 3，我们可以将选通的触发设置在时隙 3 中的突发脉冲序列的上升沿并指定选通时延为 1.4577 ms、选通脉冲宽度为461.60 μs，如图 2-38 所示。选通时延确保了在整个突发脉冲序列持续期间我们只测量时隙 3 信号的频谱。注意一定要谨慎地选择选通开始和停止值，以避开突发脉冲序列的上升沿和下降沿，因为需要在测量前留出一些时间等待 RBW 滤波信号稳定下来。图 2-39. 显示了时隙 3 的频谱，表明杂散信号并不是由此突发脉冲引起的。

实现时间选通的三种常见方法

– FFT 选通

– 本振选通

– 视频选通

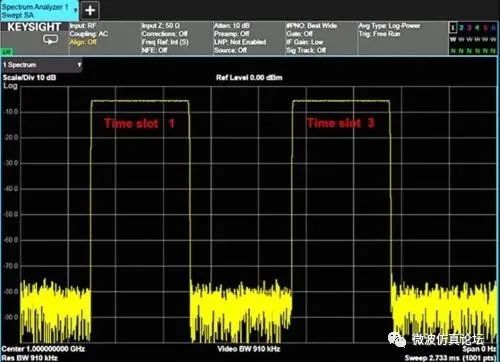
图 2-36. 只有时隙 1 和 3“开启”的 GSM 信号在零扫宽(时域)时的显示。

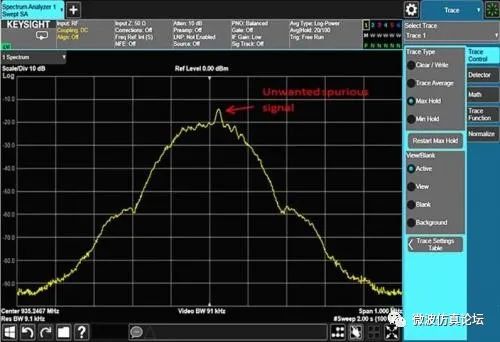
图 2-37. 两个时隙“开启”的 GSM 信号的频域显示，频谱中出现多余的杂散信号。

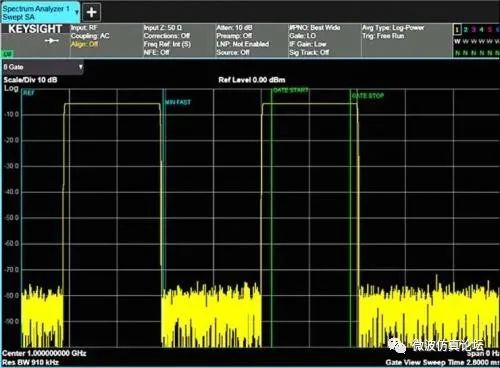
图 2-38. 使用时间选通观察 GSM 信号时隙 3 的频谱。

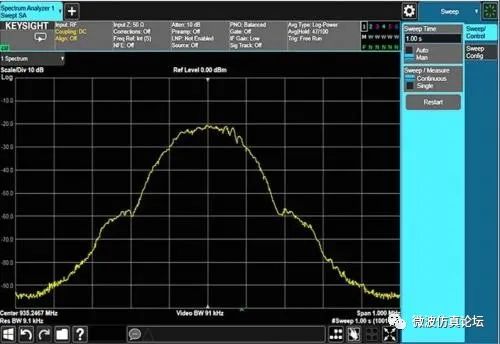
图 2-39. 时隙3 的频谱表明杂散信号不是由此突发脉冲导致的。

选通 FFT

Keysight X 系列信号分析仪具有内置的 FFT 功能。在此模式下，触发启用后经过所选时延，频谱仪开始捕获数据并进行 FFT 处理。中频信号经数字化后在 1.83/RBW 的时间周期内被采集。基于这个数据采集计算 FFT，得到信号的频谱。因此，该频谱存在于已知时间段的某个特定时间。当频谱仪扫宽比 FFT 最大宽度窄时，这是速度最快的选通技术。

为了获得尽可能大的频率分辨率，应选择频谱仪可用的最小的 RBW(它的捕获时间与待测时间周期相适应)。但实际中并非总需如此，您可以选择一个较宽的 RBW 同时相应地减小选通脉冲宽度。在 FFT选通应用中最小可用的 RBW 通常比其他选通技术的最小可用 RBW 更窄，因为在其他技术里中频必须在脉冲持续期内充分稳定，这需要比 1.83/RBW 更长的时间。

本振选通

本振选通有时也称为扫描选通，是另一项时间选通技术。在本振选通模式下，我们通过控制由扫描发生器产生的斜波电压来扫描本振，如图 2-40 所示。像所有频谱仪一样，当选通信号开启时，本振信号在频率上爬升。当选通关闭后，扫描发生器的输出电压固定，本振在频率上停止上升。由于这种技术可以在每个突发脉冲信号持续期间内对多个信号收集单元进行测量，因此它的速度比视频选通快很多。我们同样以前面提到的 GSM 信号为例。

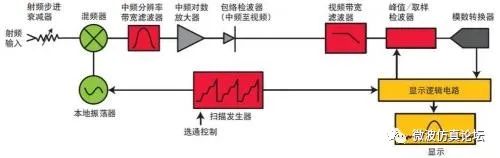
图 2-40. 在本振选通模式下，本振只在选通间隔内扫描

本振选通

本振选通有时也称为扫描选通，是另一项时间选通技术。在本振选通模式下，我们通过控制由扫描发生器产生的斜波电压来扫描本振，如图 2-40 所示。像所有频谱仪一样，当选通信号开启时，本振信号在频率上爬升。当选通关闭后，扫描发生器的输出电压固定，本振在频率上停止上升。由于这种技术可以在每个突发脉冲信号持续期间内对多个信号收集单元进行测量，因此它的速度比视频选通快很多。我们同样以前面提到的 GSM 信号为例。

用标准非选通模式的 X 系列信号分析仪扫过 1 MHz 扫宽需要 14.6 ms，如图 2-41 所示。如果选通脉冲宽度为 0.3 ms，频谱仪必须在 49(14.6 除以 0.3)个选通信号间隔时间内扫描;如果 GSM 信号的完整帧长为 4.615 ms，那么总的测量时间就等于 49 个选通信号间隔乘以 4.615 ms 等于 226 ms。这与后面所说的视频选通技术相比在速度上有了很大的提高。X 系列信号分析仪和 PSA 系列频谱分析仪均具有本振选通功能。

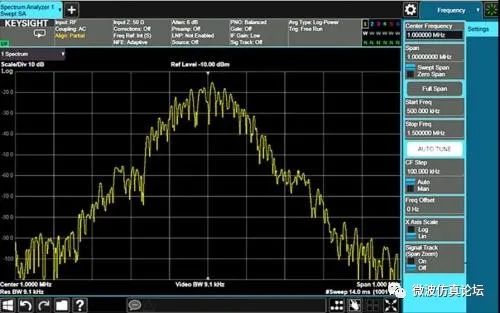
图 2-41. GSM 信号频谱

视频选通

一些频谱仪(包括 Keysight 8560、8590 和E S A 系列)采用了视频选通的信号分析技术。这种情况下，当选通信号处于截止状态时视频电压被关闭或为“负无穷大”。检波器设置为峰值检波，扫描时间的设置必须保证选通信号在每个显示点或信号收集单元内至少出现一次，从而确保峰值检波器能够获得相应时间间隔内的真实数据，否则会出现没有数据值的迹线点，进而导致不完整的显示频谱。因此，最小扫描时间 = 显示点数 N x 突发脉冲的时间周期。例如，在 GSM 测量中，完整帧长为 4.615 ms，假设 ESA 频谱仪设置为缺省显示点数 401，那么对于 GSM 视频选通测量的最小扫描时间是 401 x 4.615 ms = 1.85 s。

有些 TDMA 格式的周期时间长达 90 ms，导致如果使用视频选通技术需要很长的扫描时间。现在，您已经知道典型的模拟频谱分析仪的工作原理，以及部分重要功能特性的使用方法，接下来要讨论的是当使用数字技术替代某些模拟电路时，对频谱分析仪的性能有何改善。

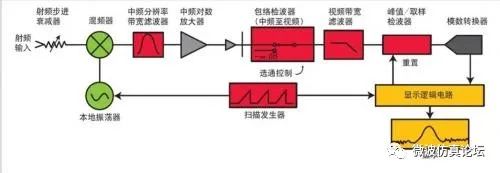
图 2-42. 具有视频选通的频谱分析仪的结构框图

原文标题：干货!一文精通频谱仪原理[20220428]

文章出处：【微信公众号：电磁兼容EMC】欢迎添加关注!文章转载请注明出处。

审核编辑：汤梓红