和求最大深度一个套路?
111.二叉树的最小深度
题目地址:https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例:
给定二叉树[3,9,20,null,null,15,7],

返回它的最小深度 2.
思路
看完了这篇104.二叉树的最大深度,再来看看如何求最小深度。
直觉上好像和求最大深度差不多,其实还是差不少的。
遍历顺序上依然是后序遍历(因为要比较递归返回之后的结果),但在处理中间节点的逻辑上,最大深度很容易理解,最小深度可有一个误区,如图:
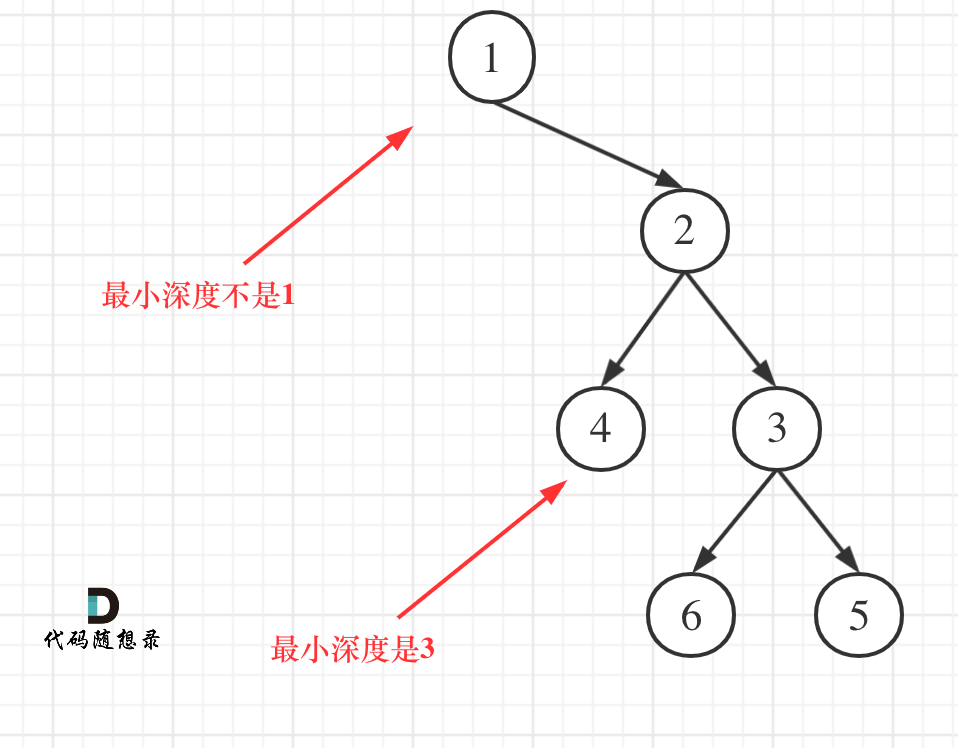
这就重新审题了,题目中说的是:最小深度是从根节点到最近叶子节点的最短路径上的节点数量。,注意是叶子节点。
什么是叶子节点,左右孩子都为空的节点才是叶子节点!
递归法
来来来,一起递归三部曲:
- 确定递归函数的参数和返回值
参数为要传入的二叉树根节点,返回的是int类型的深度。
代码如下:
intgetDepth(TreeNode*node)
- 确定终止条件
终止条件也是遇到空节点返回0,表示当前节点的高度为0。
代码如下:
if(node==NULL)return0;
- 确定单层递归的逻辑
这块和求最大深度可就不一样了,一些同学可能会写如下代码:
intleftDepth=getDepth(node->left);
intrightDepth=getDepth(node->right);
intresult=1+min(leftDepth,rightDepth);
returnresult;
这个代码就犯了此图中的误区:

如果这么求的话,没有左孩子的分支会算为最短深度。
所以,如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。
代码如下:
intleftDepth=getDepth(node->left);//左
intrightDepth=getDepth(node->right);//右
//中
//当一个左子树为空,右不为空,这时并不是最低点
if(node->left==NULL&&node->right!=NULL){
return1+rightDepth;
}
//当一个右子树为空,左不为空,这时并不是最低点
if(node->left!=NULL&&node->right==NULL){
return1+leftDepth;
}
intresult=1+min(leftDepth,rightDepth);
returnresult;
遍历的顺序为后序(左右中),可以看出:求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。
整体递归代码如下:
classSolution{
public:
intgetDepth(TreeNode*node){
if(node==NULL)return0;
intleftDepth=getDepth(node->left);//左
intrightDepth=getDepth(node->right);//右
//中
//当一个左子树为空,右不为空,这时并不是最低点
if(node->left==NULL&&node->right!=NULL){
return1+rightDepth;
}
//当一个右子树为空,左不为空,这时并不是最低点
if(node->left!=NULL&&node->right==NULL){
return1+leftDepth;
}
intresult=1+min(leftDepth,rightDepth);
returnresult;
}
intminDepth(TreeNode*root){
returngetDepth(root);
}
};
精简之后代码如下:
classSolution{
public:
intminDepth(TreeNode*root){
if(root==NULL)return0;
if(root->left==NULL&&root->right!=NULL){
return1+minDepth(root->right);
}
if(root->left!=NULL&&root->right==NULL){
return1+minDepth(root->left);
}
return1+min(minDepth(root->left),minDepth(root->right));
}
};
精简之后的代码根本看不出是哪种遍历方式,所以依然还要强调一波:如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。
迭代法
相对于104.二叉树的最大深度,本题还可以使用层序遍历的方式来解决,思路是一样的。
如果对层序遍历还不清楚的话,可以看这篇:二叉树:层序遍历登场!
需要注意的是,只有当左右孩子都为空的时候,才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
代码如下:(详细注释)
classSolution{
public:
intminDepth(TreeNode*root){
if(root==NULL)return0;
intdepth=0;
queueque;
que.push(root);
while(!que.empty()){
intsize=que.size();
depth++;//记录最小深度
for(inti=0;i< size; i++) {
TreeNode* node = que.front();
que.pop();
if(node->left)que.push(node->left);
if(node->right)que.push(node->right);
if(!node->left&&!node->right){//当左右孩子都为空的时候,说明是最低点的一层了,退出
returndepth;
}
}
}
returndepth;
}
};
其他语言版本
Java
classSolution{
/**
*递归法,相比求MaxDepth要复杂点
*因为最小深度是从根节点到最近**叶子节点**的最短路径上的节点数量
*/
publicintminDepth(TreeNoderoot){
if(root==null){
return0;
}
intleftDepth=minDepth(root.left);
intrightDepth=minDepth(root.right);
if(root.left==null){
returnrightDepth+1;
}
if(root.right==null){
returnleftDepth+1;
}
//左右结点都不为null
returnMath.min(leftDepth,rightDepth)+1;
}
}
classSolution{
/**
*迭代法,层序遍历
*/
publicintminDepth(TreeNoderoot){
if(root==null){
return0;
}
Dequedeque=newLinkedList<>();
deque.offer(root);
intdepth=0;
while(!deque.isEmpty()){
intsize=deque.size();
depth++;
for(inti=0;i< size; i++) {
TreeNode poll = deque.poll();
if(poll.left==null&&poll.right==null){
//是叶子结点,直接返回depth,因为从上往下遍历,所以该值就是最小值
returndepth;
}
if(poll.left!=null){
deque.offer(poll.left);
}
if(poll.right!=null){
deque.offer(poll.right);
}
}
}
returndepth;
}
}
Python
递归法:
classSolution:
defminDepth(self,root:TreeNode)->int:
ifnotroot:
return0
ifnotroot.leftandnotroot.right:
return1
min_depth=10**9
ifroot.left:
min_depth=min(self.minDepth(root.left),min_depth)#获得左子树的最小高度
ifroot.right:
min_depth=min(self.minDepth(root.right),min_depth)#获得右子树的最小高度
returnmin_depth+1
迭代法:
classSolution:
defminDepth(self,root:TreeNode)->int:
ifnotroot:
return0
que=deque()
que.append(root)
res=1
whileque:
for_inrange(len(que)):
node=que.popleft()
#当左右孩子都为空的时候,说明是最低点的一层了,退出
ifnotnode.leftandnotnode.right:
returnres
ifnode.leftisnotNone:
que.append(node.left)
ifnode.rightisnotNone:
que.append(node.right)
res+=1
returnres审核编辑 :李倩
-
节点
+关注
关注
0文章
220浏览量
24595 -
函数
+关注
关注
3文章
4352浏览量
63261 -
二叉树
+关注
关注
0文章
74浏览量
12425
原文标题:二叉树的最小深度!
文章出处:【微信号:TheAlgorithm,微信公众号:算法与数据结构】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
机器人看点:宇树科技王兴兴回上海母校 加速商业化落地 宇树机器人二手租赁火爆
BP神经网络与深度学习的关系
宇树科技在物联网方面
嵌入式学习-飞凌嵌入式ElfBoard ELF 1板卡-初识设备树之设备树组成和结构
飞凌嵌入式ElfBoard ELF 1板卡-初识设备树之设备树组成和结构
MCU最小系统电路设计指南

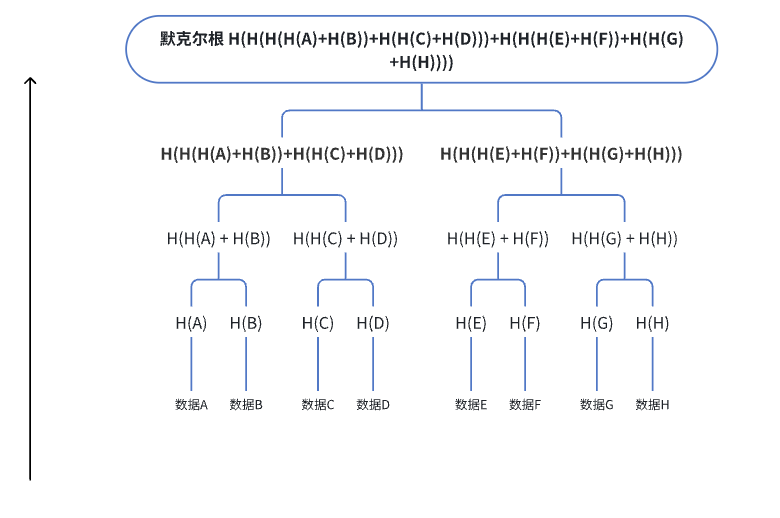
什么是默克尔树(Merkle Tree)?如何计算默克尔根?
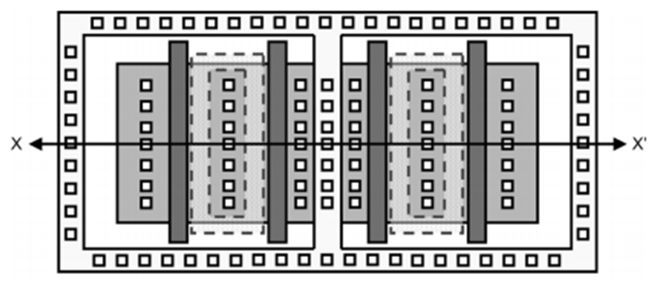
多叉指MOSFET器件静电防护鲁棒性提升技巧
示波器怎么设置存储深度?
原理图设计里两颗重要的树(国产EDA)
圣诞树灯电路图分享




 二叉树的最小深度
二叉树的最小深度











评论