1、为什么要重视电源噪声问题
芯片内部有成千上万个晶体管,这些晶体管组成内部的门电路、组合逻辑、寄存器、计 数器、延迟线、状态机、以及其他逻辑功能。随着芯片的集成度越来越高,内部晶体管数 越来越大。芯片的外部引脚数有限,为一个晶体管提供单独的供电引脚是不现实的。芯 片的外部电源引脚提供给内部晶体管一个公共的供电节点, 因此内部晶体管状态的转换必 然引起电源噪声在芯片内部的传递。
对内部各个晶体管的操作通常由内核时钟或片内外设时钟同步, 但是由于内部延时的 差别,各个晶体管的状态转换不可能是严格同步的,当某些晶体管已完成了状态转换,另 一些晶体管可能仍处于转换过程中。芯片内部处于高电平的门电路会把电源噪声传递到其 他门电路的输入部分。如果接受电源噪声的门电路此时处于电平转换的不定态区域,那么电 源噪声可能会被放大,并在门电路的输出端产生矩形脉冲干扰,进而引起电路的逻辑错误。芯片外部电源引脚处的噪声通过内部门电路的传播,还可能会触发内部寄存器产生状态转换。
除了对芯片本身工作状态产生影响外,电源噪声还会对其他部分产生影响。比如电源噪 声会影响晶振、PLL、DLL 的抖动特性,AD 转换电路的转换精度等。
由于最终产品工作温度的变化以及生产过程中产生的不一致性,如果是由于电源系统产 生的问题,电路将非常难调试,因此最好在电路设计之初就遵循某种成熟的设计规则,使电 源系统更加稳健。
2、电源系统噪声余分析
绝大多数芯片都会给出一个正常工作的电压范围,这个值通常是±5%。例如:对于 3.3V 电压,为满足芯片正常工作,供电电压在 3.13V 到 3.47V 之间,或 3.3V±165mV。对于 1.2V 电压,为满足芯片正常工作,供电电压在 1.14V 到 1.26V 之间,或 1.2V±60mV。这些限 制可以在芯片 datasheet 中的 recommended operating conditions 部分查到。这些限制要考 虑两个部分,第一是稳压芯片的直流输出误差,第二是电源噪声的峰值幅度。老式的稳压芯 片的输出电压精度通常是±2.5%,因此电源噪声的峰值幅度不应超过±2.5%。当然随着芯片 工艺的提高,现代的稳压芯片直流精度更高,可能会达到±1%以下,TI 公司的开关电源芯 片 TPS54310 精度可达±1%,线性稳压源 AMS1117 可达±0.2%。但是要记住,达到这样 的精度是有条件的,包括负载情况,工作温度等限制。因此可靠的设计还是以±2.5%这个值 更把握些。如果你能确保所用的芯片安装到电路板上后能达到更高的稳压精度,那么你可以 为你的这款设计单独进行噪声余计算。本文着重电源部分设计的原理说明,电源噪声余 将使用±2.5%这个值。
电源噪声余计算非常简单,方法如下:
比如芯片正常工作电压范围为 3.13V~3.47V 之间,稳压芯片标称输出 3.3V。安装到 电路板上后,稳压芯片输出 3.36V。那么容许电压变化范围为 3.47-3.36=0.11V=110mV。稳 压芯片输出精度±1%,即±3.36*1%=±33.6 mV。电源噪声余为 110-33.6=76.4 mV。
计算很简单,但是要注意四个问题:
第一,稳压芯片输出电压能精确的定在 3.3V 么?外围器件如电阻电容电感的参数也不 是精确的,这对稳压芯片的输出电压有影响,所以这里用了 3.36V 这个值。在安装到电路板上之前,你不可能预测到准确的输出电压值。
第二, 工作环境是否符合稳压芯片手册上的推荐环境?器件老化后参数还会和芯片手 册上的一致么?
第三,负载情况怎样?这对稳压芯片的输出电压也有影响。
第四,电源噪声最终会影响到信号质。而信号上的噪声来源不仅仅是电源噪声,反射 串扰等信号完整性问题也会在信号上叠加噪声,不能把所有噪声余都分配给电源系统。所 以,在设计电源噪声余的时候要留有余地。
另一个重要问题是:不同电压等级,对电源噪声余要求不一样,按±2.5%计算的话, 1.2V 电压等级的噪声余只有 30mV。这是一个很苛刻的限制,设计的时候要谨慎些。模 拟电路对电源的要求更高。电源噪声影响时钟系统,可能会引起时序匹配问题。因此必须重 视电源噪声问题。
3、电源噪声是如何产生的?
电源系统的噪声来源有三个方面:
第一,稳压电源芯片本身的输出并不是恒定的,会有一定的波纹。这是由稳压芯片自身 决定的,一旦选好了稳压电源芯片,对这部分噪声我们只能接受,无法控制。
第二,稳压电源无法实时响应负载对于电流需求的快速变化。稳压电源芯片通过感知其 输出电压的变化,调整其输出电流,从而把输出电压调整到额定输出值。多数常用的稳压源 调整电压的时间在 ms~us 级。因此,对于负载电流变化频率在直流到几百 KHz 之间时,稳 压源可以很好的做出调整,保持输出电压的稳定。当负载瞬态电流变化频率超出这一范围时, 稳压源的电压输出会出现跌落,从而产生电源噪声。现在,微处理器的内核及外设的时钟频 率已超过了 600 MHz,内部晶体管电平转换时间下降到 800 ps 以下。这要求电源分配系 统必须在直流到 1GHz 范围内都能快速响应负载电流的变化, 但现有稳压电源芯片不可能 满足这一苛刻要求。我们只能用其他方法补偿稳压源这一不足,这涉及到后面要讲的电源去耦。
第三,负载瞬态电流在电源路径阻抗和地路径阻抗上产生的压降。PCB 板上任何电气 路径不可避免的会存在阻抗,不论是完整的电源平面还是电源引线。对于多层板,通常提供 一个完整的电源平面和地平面,稳压电源输出首先接入电源平面,供电电流流电源平面, 到达负载电源引脚。地路径和电源路径类似,只不过电流路径变成了地平面。完整平面的阻 抗很低,但确实存在。如果不使用平面而使用引线,那么路径上的阻抗会更高。另外,引脚 及焊盘本身也会有寄生电感存在,瞬态电流流此路径必然产生压降,因此负载芯片电源引 脚处的电压会随着瞬态电流的变化而波动,这就是阻抗产生的电源噪声。在电源路径表现为 负载芯片电源引脚处的电压轨道塌陷, 在地路径表现为负载芯片地引脚处的电位和参考地 电位不同 (注意,这和地弹不同,地弹是指芯片内部参考地电位相对于板级参考地电位的 跳变)
4、电容退耦的两种解释
采用电容退耦是解决电源噪声问题的主要方法。这种方法对提高瞬态电流的响应速度, 降低电源分配系统的阻抗都非常有效。
对于电容退耦, 很多资料中都有涉及, 但是阐述的角度不同。有些是从局部电荷存 储 (即储能)的角度来说明,有些是从电源分配系统的阻抗的角度来说明,还有些资料的说明更为混乱,一会提储能,一会提阻抗,因此很多人在看资料的时候感到有些迷惑。其实, 这两种提法,本质上是相同的,只不过看待问题的视角不同而已。为了让大家有个清楚的认 识,本文分别介绍一下这两种解释。
4.1 从储能的角度来说明电容退耦原理。
在制作电路板时, 通常会在负载芯片周围放置很多电容, 这些电容就起到电源退耦作 用。其原理可用图 1 说明。
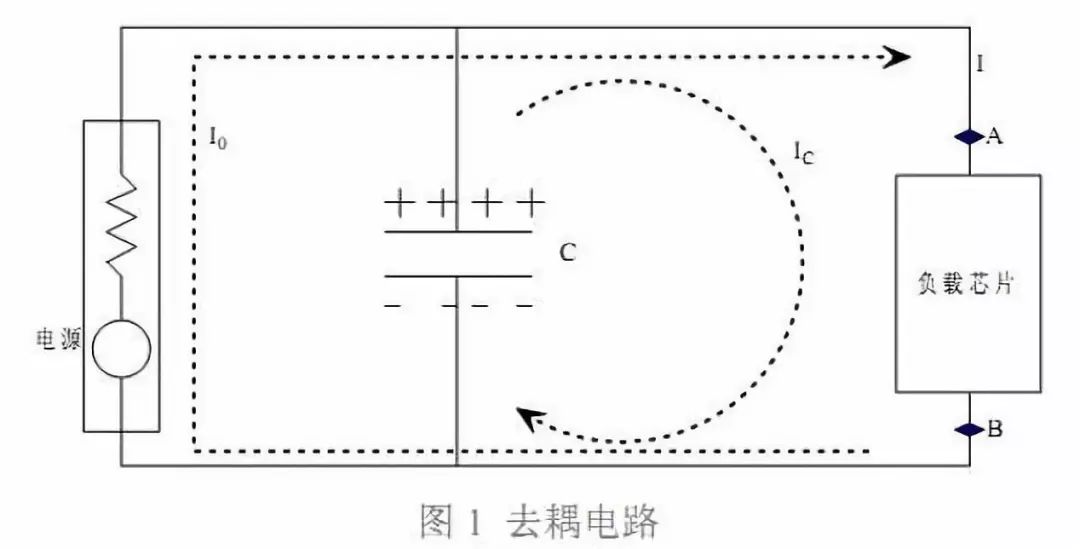
当负载电流不变时,其电流由稳压电源部分提供,即图中的 I0,方向如图所示。此时 电容两端电压与负载两端电压一致,电流 Ic 为 0,电容两端存储相当数的电荷,其电荷 数和电容有关(C=Q/U)。当负载瞬态电流发生变化时,由于负载芯片内部晶体管电平 转换速度极快,必须在极短的时间内为负载芯片提供足够的电流。但是稳压电源无法很快 响应负载电流的变化,因此,电流 I0不会马上满足负载瞬态电流要求,因此负载芯片电压 会降低。但是由于电容电压与负载电压相同,因此电容两端存在电压变化。对于电容来说电 压变化必然产生电流,此时电容对负载放电,电流 Ic 不再为 0,为负载芯片提供电流。根 据电容等式:
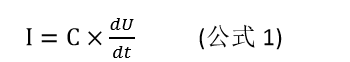
只要电容 C 足够大,只需很小的电压变化,电容就可以提供足够大的电流,满足负 载瞬态电流的要求。这样就保证了负载芯片电压的变化在容许的范围内。这里,相当于电容 预先存储了一部分电能,在负载需要的时候释放出来,即电容是储能元件。储能电容的存在 使负载消耗的能得到快速补充,因此保证了负载两端电压不至于有太大变化,此时电容担 负的是局部电源的角色。
从储能的角度来理解电源退耦,非常直观易懂,但是对电路设计帮助不大。从阻抗的角 度理解电容退耦,能让我们设计电路时有章可循。实际上,在决定电源分配系统的去耦电容 的时候,用的就是阻抗的概念。
4.2 从阻抗的角度来理解退耦原理。
将图 1 中的负载芯片拿掉,如图 2 所示。从 AB 两点向左看过去,稳压电源以及电容退耦系统一起,可以看成一个复合的电源系统。这个电源系统的特点是:不论 AB 两点间 负载瞬态电流如何变化,都能保证 AB 两点间的电压保持基本稳定,即 AB 两点间电压变 化很小。
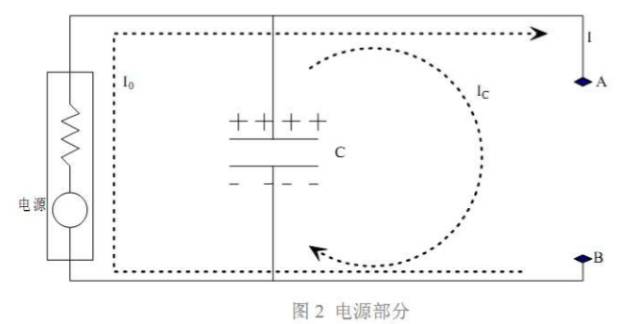
我们可以用一个等效电源模型表示上面这个复合的电源系统,如图 3
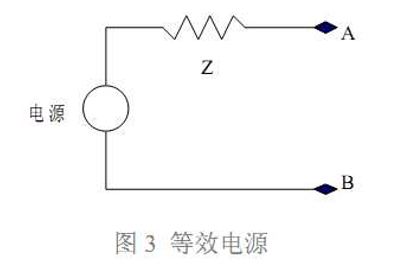
对于这个电路可写出如下等式:

我们的最终设计目标是,不论 AB 两点间负载瞬态电流如何变化,都要保持 AB 两点 间电压变化范围很小,根据公式 2,这个要求等效于电源系统的阻抗 Z 要足够低。在图 2 中,我们是通过去耦电容来达到这一要求的,因此从等效的角度出发,可以说去耦电容降低 了电源系统的阻抗。另一方面,从电路原理的角度来说,可得到同样结论。电容对于交流信 号呈现低阻抗特性,因此加入电容,实际上也确实降低了电源系统的交流阻抗(1/jwc)。
从阻抗的角度理解电容退耦,可以给我们设计电源分配系统带来极大的方便。实际上, 电源分配系统设计的最根本的原则就是使阻抗最小。最有效的设计方法就是在这个原则指 导下产生的。
5、实际电容的特性
正确使用电容进行电源退耦,必须了解实际电容的频率特性。理想电容器在实际中是不存在的,这就是为什么常听到“电容不仅仅是电容”的原因。
实际的电容器总会存在一些寄生参数,这些寄生参数在低频时表现不明显,但是高频情 况下,其重要性可能会超过容值本身。图 4 是实际电容器的 SPICE 模型,图中,ESR 代表 等效串联电阻,ESL 代表等效串联电感或寄生电感,C 为理想电容。
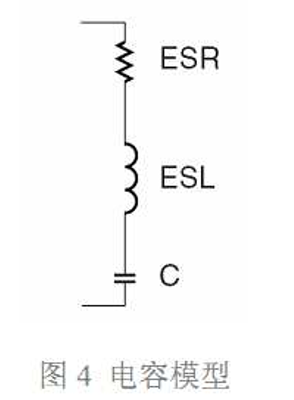
等效串联电感(寄生电感)无法消除,只要存在引线,就会有寄生电感。这从磁场能 变化的角度可以很容易理解,电流发生变化时,磁场能发生变化,但是不可能发生能跃 变,表现出电感特性。寄生电感会延缓电容电流的变化,电感越大,电容充放电阻抗就越大, 反应时间就越长。等效串联电阻也不可消除的,很简单,因为制作电容的材料不是超导体。讨论实际电容特性之前,首先介绍谐振的概念。对于图 4 的电容模型,其复阻抗为:
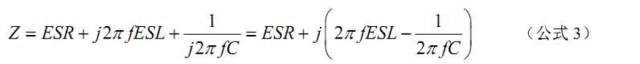
当频率很低时,2πf ESL < 1/ 2πfC,整个电容器表现为电容性,
当频率很高时,2πf ESL > 1/ 2πfC,电容器此时表现为电感性,因此“高频时电容不再 是电容” ,而呈现为电感。当

此时容性阻抗矢与感性阻抗之差为 0,电容的总阻抗最小,表现为纯电阻特性。该频 率点就是电容的自谐振频率。自谐振频率点是区分电容是容性还是感性的分界点, 高于谐 振频率时, “电容不再是电容” , 因此退耦作用将下降。因此,实际电容器都有一定的 工作频率范围,只有在其工作频率范围内,电容才具有很好的退耦作用,使用电容进行电源 退耦时要特别关注这一点。寄生电感(等效串联电感)是电容器在高于自谐振频率点之后退 耦功能被消弱的根本原因。图 5 显示了一个实际的 0805 封装 0.1uF 陶瓷电容,其阻抗随 频率变化的曲线。
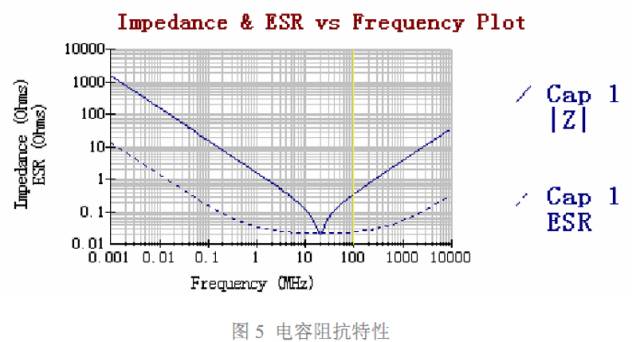
电容的自谐振频率值和它的电容值及等效串联电感值有关,使用时可查看器件手册,了 解该项参数,确定电容的有效频率范围。下面列出了 AVX 生产的陶瓷电容不同封装的各项 参数值。
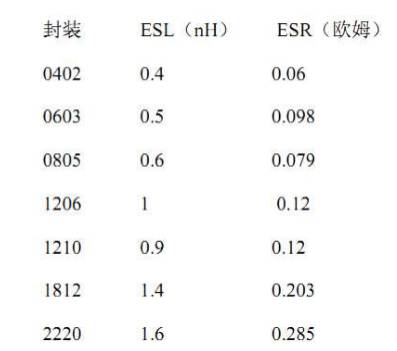
电容的等效串联电感和生产工艺和封装尺寸有关,同一个厂家的同种封装尺寸的电容, 其等效串联电感基本相同。通常小封装的电容等效串联电感更低,宽体封装的电容比窄体封 装的电容有更低的等效串联电感。
既然电容可以看成 RLC 串联电路,因此也会存在品质因数,即 Q 值,这也是在使用电 容时的一个重要参数。
电路在谐振时容抗等于感抗,所以电容和电感上两端的电压有效值必然相等,电容上的 电压有效值 UC=I*1/ωC=U/ωCR=QU,品质因数 Q=1/ωCR,这里 I 是电路的总电流。电感 上的电压有效值 UL=ωL*I=ωL*U/R=QU, 品质因数 Q=ωL/R。因为:UC=UL 所以 Q=1/ω CR=ωL/R。电容上的电压与外加信号电压 U 之比 UC/U=(I*1/ωC)/RI=1/ωCR=Q。电感上 的电压与外加信号电压 U 之比 UL/U=ωLI/RI=ωL/R=Q。从上面分析可见,电路的品质因数 越高,电感或电容上的电压比外加电压越高。
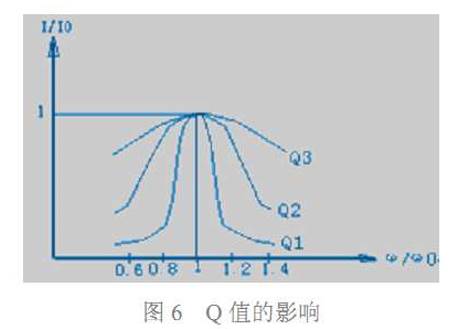
Q 值影响电路的频率选择性。当电路处于谐振频率时,有最大的电流,偏离谐振频率时 总电流小。我们用 I/I0 表示通过电路的电流与谐振电路中电流的比值,即相对变化率。ω/ω0 表示频率偏离谐振频率程度。图 6 显示了 I/I0 与ω/ω0关系曲线。这里有三条曲线, 对应三个不同的 Q 值,其中有 Q1>Q2>Q3。从图中可看出当外加信号频率 ω 偏离电路的 谐振频率 ω0 时,I/I0 均小于 1。Q 值越高在一定的频偏下电流下降得越快,其谐振曲线 越尖锐。也就是说电路的选择性是由电路的品质因素 Q 所决定的,Q 值越高选择性越好。在电路板上会放置一些大的电容,通常是坦电容或电解电容。这类电容有很低的 ESL,但是 ESR 很高,因此 Q 值很低,具有很宽的有效频率范围,非常适合板级电源滤波。
6、电容的安装谐振频率
上一节介绍的是电容自身的参数, 当电容安装到电路板上后, 还会引入额外的寄生参 数,从而引起谐振频率的偏移。充分理解电容的自谐振频率和安装谐振频率非常重要,在计 算系统参数时,实际使用的是安装谐振频率,而不是自谐振频率,因为我们关注的是电容安 装到电路板上之后的表现。
电容在电路板上的安装通常包括一小段从焊盘拉出的引出线,两个或更多的过孔。我们 知道,不论引线还是过孔都存在寄生电感。寄生电感是我们主要关注的重要参数,因为它对 电容的特性影响最大。电容安装后,可以对其周围一小片区域有效去耦,这涉及到去耦半径 问题,本文后面还要详细讲述。现在我们考察这样一种情况,电容要对距离它 2 厘米处的 一点去耦,这时寄生电感包括哪几部分。首先,电容自身存在寄生电感。从电容到达需要去 耦区域的路径上包括焊盘、一小段引出线、过孔、2 厘米长的电源及地平面,这几个部分都 存在寄生电感。相比较而言,过孔的寄生电感较大。可以用公式近似计算一个过孔的寄生电 感有多大。 公式为
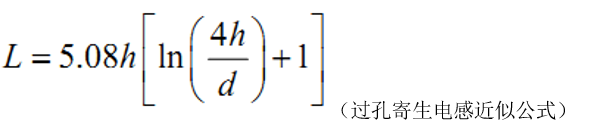
其中:L 是过孔的寄生电感,单位是 nH。h 为过孔的长度,和板厚有关,单位是英寸。d 为过孔的直径,单位是英寸。下面就计算一个常见的过孔的寄生电感,看看有多大,以便 有一个感性认识。设过孔的长度为 63mil(对应电路板的厚度 1.6 毫米,这一厚度的电路板 很常见) ,过孔直径 8mil,根据上面公式得:
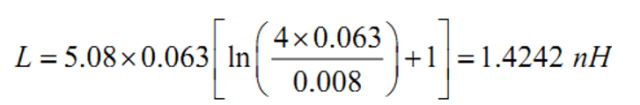
这一寄生电感比很多小封装电容自身的寄生电感要大, 必须考虑它的影响。过孔的直 径越大,寄生电感越小。过孔长度越长,电感越大。下面我们就以一个 0805 封装 0.01uF 电容为例,计算安装前后谐振频率的变化。参数如下:容值:C=0.01uF。电容自身等效 串联电感:ESL=0.6 nH。安装后增加的寄生电感:Lmount=1.5nH。
电容的自谐振频率:
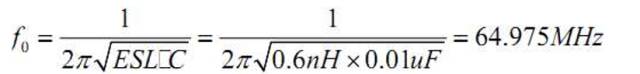
安装后的总寄生电感:0.6+1.5=2.1nH。注意,实际上安装一个电容至少要两个过孔,寄 生电感是串联的,如果只用两个过孔,则过孔引入的寄生电感就有 3nH。但是在电容的 一端都并联几个过孔,可以有效小总的寄生电感,这和安装方法有关。
安装后的谐振频率为:
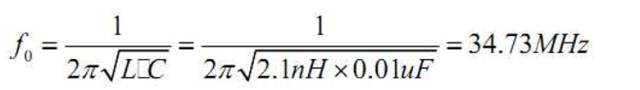
可见,安装后电容的谐振频率发生了很大的偏移,使得小电容的高频去耦特性被消弱。在进行电路参数设计时,应以这个安装后的谐振频率计算,因为这才是电容在电路板上的实 际表现。
安装电感对电容的去耦特性产生很大影响,应尽小。实际上,如何最大程度的小 安装后的寄生电感,是一个非常重要的问题,本文后面还要专门讨论。
7、局部去耦设计方法
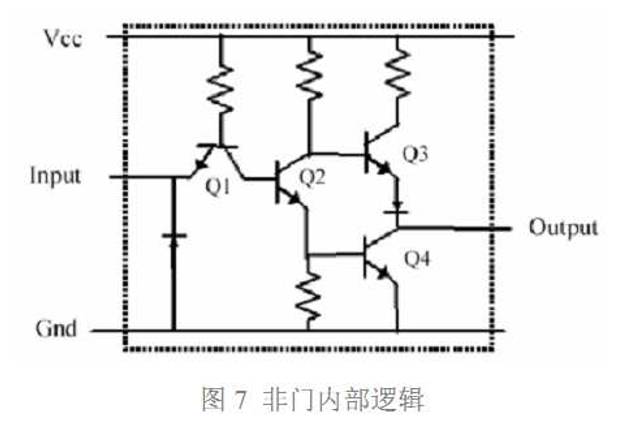
我们从一个典型逻辑电路入手,讨论局部退耦设计方法。图 7 是典型的非门(NOT GATE) 电路。当输入(Input)低电平时,Q1 打开,拉低 Q2 的基极,因此 Q4 的基极被拉低, Q3 打开,输出(Output)高电平。
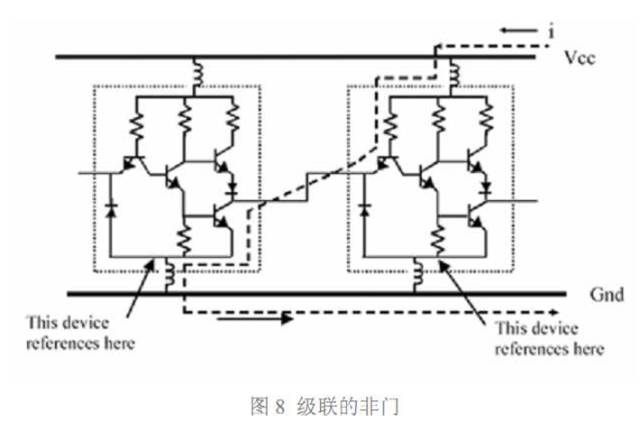
实际电路设计中,器件之间相互连接构成完整系统,因此器件之间必然存在相互影响。作为例子,我们级联两个非门,如图 8 所示,看看两个器件之间怎样相互影响。理想的情 况应该是:第一个非门输入逻辑低电平(逻辑 0) ,其输出为高电平,第二个非门输入为 第一个的输出,也为高电平,因此第二个非门输出低电平。
为保证逻辑电路能正常工作,表征电路逻辑状态的电平值必须落在一定范围内。比如对 于 3.3V 逻辑,高电平大于 2V 为逻辑 1,低电平小于 0.8V 为逻辑 0。当逻辑门电路的输 入电平处于上述范围内时,电路能保证对输入逻辑状态的正确判断。当电平值处于 0.8V 到 2V 之间时,则不能保证对输入逻辑状态的正确判断,对于本例的非门来说,其输出可能是 逻辑 0,也可能是逻辑 1,或者处于不定态。因此输入电平超出规定范围时,可能发生逻辑 错误。
逻辑电路在设计时采用了很多技术来保证器件本身不会发生这样的错误。但是,当器件 安装到电路板上,板级系统的其他因素仍可能导致类似错误的发生。图 8 中级联的两个非 门共用电源端 Vcc 和接地端 GND。Vcc 到个非门供电引脚间都会存在寄生电感,个非 门的地引脚到 GND 之间也同样存在寄生电感。在实际板级电路中设计中, 寄生电感不可 避免,电源平面、地平面、过孔、焊盘、连接焊盘的引出线都会引入额外的寄生电感。图 8 已画出了电源端和地端的寄生电感。当第一个非门输入高电平,其输出低电平。此时将会 形成图中虚线所示的电流通路,第一个非门接地处寄生电感上的电压为:
V=L*di/dt
这里 i 为逻辑转换过程形成的瞬态电流。如果电路转换过程非常快(高速器件内部晶 体管转换时间已降到了皮秒级) ,di/dt 将是个很大的值,即使很小的寄生电感 L 也会 在电感两端感应出很大的电压 V。对于一些大规模逻辑芯片,接地引脚是内部非常多的晶 体管共用的,这些晶体管同时开关的话,将产生很大的瞬态电流,再加上极快的转换时间, 寄生电感上的感应电压更大。此时第一个非门的输出信号电平为:非门本身低电平电压+寄 生电感上的电压。如果这一值接近 2V,可能会被第二个非门判断为逻辑 1,从而发生逻辑 错误。
寄生电感可能引起电路逻辑错误,那么如何解决这一问题?
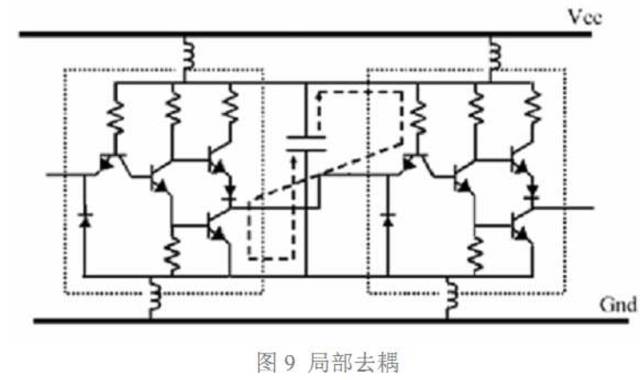
图 9 展示了一种解决方法。把电容紧邻器件放置,跨接在电源引脚和地引脚之间。正 常时,电容充电,存储一部分电荷。当非门发生翻转瞬间,电容放电,形成瞬间的浪涌电流, 方向如图 9 中虚线所示。这样电路转换所需的瞬态电流不必再由 VCC 提供,电容相当于局 部小电源。因此电源端和地端的寄生电感被旁路掉了,寄生电感在这一瞬间没有电流流过, 因而也不存在感应电压,这就保证了第一个非门输出信号的逻辑电平值的正确性。
所需电容可能不是一个,通常是两个或多个电容并联放置,小电容本身的串联电 感,进而小电容充放电回路的阻抗。电容的摆放、安装距离、安装方法、电容选择等 问题,本文后面会详细介绍。
很多芯片制造商在参考设计中给出的都是这种局部去耦方式, 但并不是说这种方 式就是最优的。芯片商关心的是如何提高他所提供的特定器件的性能,也就是说,着眼 点在器件本身,并没有从整个电路系统的角度来处理电源去耦的问题。有时你会发现, 对一个的电源和地引脚都单独去耦是不现实的,可能是空间限制,放不下如此多的电容,也可能是成本限制。因此对于板级集成的工程师来说,除了要熟悉局部去耦的方法 外,还要深入研究如何从整个电源分配系统的角度进行电源去耦设计。
8、从电源系统的角度进行去耦设计
先插一句题外话,很多人在看资料时会有这样的困惑,有的资料上说要对个电源 引脚加去耦电容,而另一些资料并不是按照个电源引脚都加去偶电容来设计的,只是 说在芯片周围放置多少电容,然后怎么放置,怎么打孔等等。那么到底哪种说法及做法 正确呢?我在刚接触电路设计的时候也有这样的困惑。其实,两种方法都是正确的,只 不过处理问题的角度不同。看过本文后,你就彻底明白了。
上一节讲了对引脚去耦的方法,这一节就来讲讲另一种方法,从电源系统的角度进 行去耦设计。该方法本着这样一个原则:在感兴趣的频率范围内, 使整个电源分配 系统阻抗最低。其方法仍然是使用去耦电容。
电源去耦涉及到很多问题:总的电容多大才能满足要求?如何确定这个值?选 择那些电容值?放多少个电容?选什么材质的电容?电容如何安装到电路板上?电容 放置距离有什么要求?下面分别介绍。
8.1 著名的 Target Impedance(目标阻抗)
目标阻抗(Target Impedance)定义为:
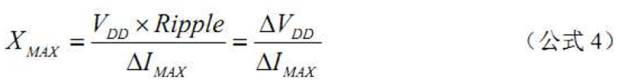
其中:Vdd 为要进行去耦的电源电压等级,常见的有 5V、3.3V、1.8V、1.26V、1.2V 等。Ripple 为允许的电压波动,在电源噪声余一节中我们已阐述过了,典型值为 2.5%。
∆IMAX 为负载芯片的最大瞬态电流变化。
该定义可解释为:能满足负载最大瞬态电流供应,且电压变化不超过最大容许波动 范围的情况下,电源系统自身阻抗的最大值。超过这一阻抗值,电源波动将超过容许范 围。如果你对阻抗和电压波动的关系不清楚的话,请回顾“电容退耦的两种解释”一节。
对目标阻抗有两点需要说明
1 目标阻抗是电源系统的瞬态阻抗,是对快速变化的电流表现出来的一种阻抗特性。
2 目标阻抗和一定宽度的频段有关。在感兴趣的整个频率范围内,电源阻抗都不 能超过这个值。阻抗是电阻、电感和电容共同作用的结果,因此必然与频率有关。感兴 趣的整个频率范围有多大?这和负载对瞬态电流的要求有关。顾名思义,瞬态电流是指 在极短时间内电源必须提供的电流。如果把这个电流看做信号的话, 相当于一个阶跃信号, 具有很宽的频谱,这一频谱范围就是我们感兴趣的频率范围。
如果暂时不理解上述两点,没关系,继续看完本文后面的部分,你就明白了。
8.2 需要多大的电容
有两种方法确定所需的电容。第一种方法利用电源驱动的负载计算电容。这种 方法没有考虑 ESL 及 ESR 的影响,因此很不精确,但是对理解电容的选择有好处。第二种方法就是利用目标阻抗(Target Impedance)来计算总电容,这是业界通用的 方法,得到了广泛验证。你可以先用这种方法来计算,然后做局部微调,能达到很好的 效果,如何进行局部微调,是一个更高级的话题。下面分别介绍两种方法。
方法一:利用电源驱动的负载计算电容
设负载(容性)为 30pF,要在 2ns 内从 0V 驱动到 3.3V,瞬态电流为:
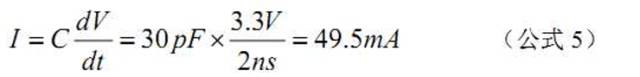
如果共有 36 个这样的负载需要驱动,则瞬态电流为:36*49.5mA=1.782A。假设容 许电压波动为:3.3*2.5%=82.5 mV,所需电容为
C=I*dt/dv=1.782A*2ns/0.0825V=43.2nF
说明:所加的电容实际上作为抑制电压波纹的储能元件,该电容必须在 2ns 内为 负载提供 1.782A 的电流, 同时电压下降不能超过 82.5 mV, 因此电容值应根据 82.5 mV 来计算。记住:
电容放电给负载提供电流,其本身电压也会下降,但是电压下降的不能超过 82.5 mV(容许的电压波纹) 。这种计算没什么实际意义,之所以放在这里说一下,是为了 让大家对去耦原理认识更深。
方法二:利用目标阻抗计算电容(设计思想很严谨,要吃透)
为了清楚的说明电容的计算方法,我们用一个例子。要去耦的电源为 1.2V,容 许电压波动为 2.5%,最大瞬态电流 600mA,
第一步:计算目标阻抗
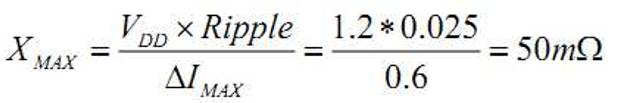
第二步:确定稳压电源频率响应范围。
和具体使用的电源片子有关,通常在 DC 到几百 kHz 之间。这里设为 DC 到 100kHz。在 100kHz 以下时,电源芯片能很好的对瞬态电流做出反应,高于 100kHz 时, 表现为很高的阻抗,如果没有外加电容,电源波动将超过允许的 2.5%。为了在高于 100kHz 时仍满足电压波动小于 2.5%要求,应该加多大的电容?
第三步:计算 bulk 电容
当频率处于电容自谐振点以下时,电容的阻抗可近似表示为:
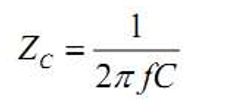
频率 f 越高,阻抗越小,频率越低,阻抗越大。在感兴趣的频率范围内,电容的 最大阻抗不能超过目标阻抗,因此使用 100kHz 计算(电容起作用的频率范围的最低频率,对应电容最高阻抗)。
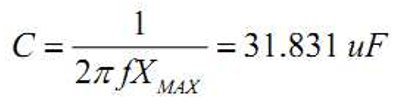
当频率处于电容自谐振点以上时,电容的阻抗可近似表示为:
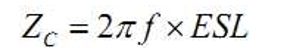
频率 f 越高,阻抗越大,但阻抗不能超过目标阻抗。假设 ESL 为 5nH,则最高有 效频率为:
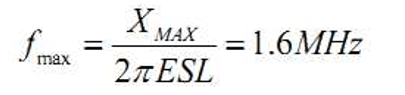
如果希望电源系统在 500MHz 以下时都能满足电压波动要求,就必须控制电容的 寄生电感。必须满足 2πf×Lmax≤XMAX ,所以有:
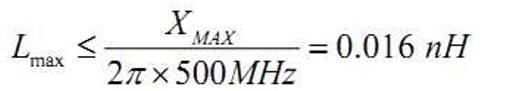
假设使用 AVX 公司的 0402 封装陶瓷电容,寄生电感约为 0.4nH,加上安装到电 路板上后过孔的寄生电感(本文后面有计算方法)假设为 0.6nH,则总的寄生电感为 1 nH。为了满足总电感不大于 0.16 nH 的要求,我们需要并联的电容个数为:1/0.016=62.5 个,因此需要 63 个 0402 电容。
为了在 1.6MHz 时阻抗小于目标阻抗,需要电容为:

因此个电容的电容为 1.9894/63=0.0316 uF。
综上所述,对于这个系统,我们选择 1 个 31.831 uF 的大电容和 63 个 0.0316 uF 的小电容即可满足要求。
注意:以上基于目标阻抗(Target Impedance)的计算,只是为了说明这种方法的 基本原理,实际中不能这样简单的计算就了事,因为还有很多问题需要考虑。学习的重 点是这种方法的核心思想。
8.3 相同容值电容的并联
使用很多电容并联能有效地小阻抗。63 个 0.0316 uF 的小电容 (个电容 ESL 为 1 nH)并联的效果相当于一个具有 0.159 nH ESL 的 1.9908 uF 电容。
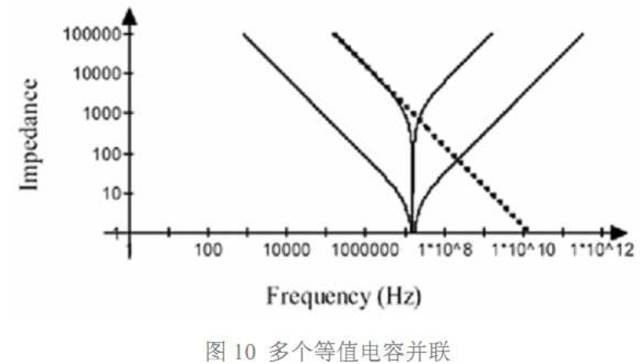
单个电容及并联电容的阻抗特性如图 10 所示。并联后仍有相同的谐振频率,但是 并联电容在一个频率点上的阻抗都小于单个电容。
但是,从图中我们看到,阻抗曲线呈 V 字型,随着频率偏离谐振点,其阻抗仍然 上升的很快。要在很宽的频率范围内满足目标阻抗要求,需要并联大的同值电容。这 不是一种好的方法,造成极大地浪费。有些人喜欢在电路板上放置很多 0.1uF 电容,如 果你设计的电路工作频率很高,信号变化很快,那就不要这样做,最好使用不同容值的 组合来构成相对平坦的阻抗曲线。
8.4 不同容值电容的并联与反谐振(Anti-Resonance)
容值不同的电容具有不同的谐振点。图 11 画出了两个电容阻抗随频率变化的曲线。
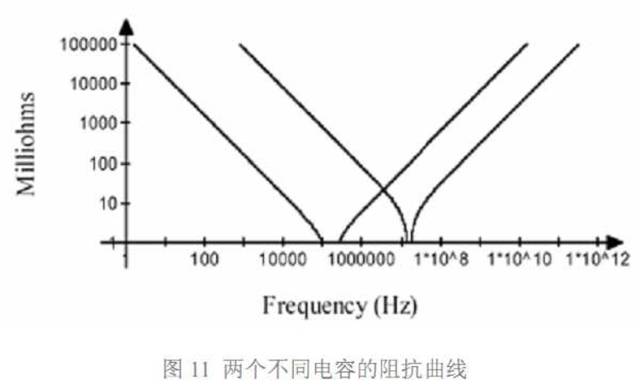
左边谐振点之前,两个电容都呈容性,右边谐振点后,两个电容都呈感性。在两个谐振 点之间,阻抗曲线交叉,在交叉点处,左边曲线代表的电容呈感性,而右边曲线代表的电容 呈容性,此时相当于 LC 并联电路。对于 LC 并联电路来说,当 L 和 C 上的电抗相等时, 发生并联谐振。因此,两条曲线的交叉点处会发生并联谐振,这就是反谐振效应,该频率点 为反谐振点。电导 G=jwc2+1/jwL1,未考虑 ESR
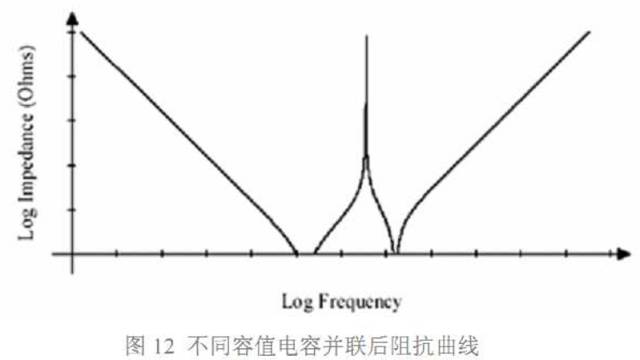
两个容值不同的电容并联后, 阻抗曲线如图 12 所示。从图 12 中我们可以得出两个结论:
a 不同容值的电容并联, 其阻抗特性曲线的底部要比图 10 阻抗曲线的底部平坦得多 (虽 然存在反谐振点,有一个阻抗尖峰) ,因而能更有效地在很宽的频率范围内小阻抗。
b 在反谐振(Anti-Resonance)点处,并联电容的阻抗值无限大,高于两个电容任何一个单 独作用时的阻抗。并联谐振或反谐振现象是使用并联去耦方法的不足之处。
在并联电容去耦的电路中, 虽然大多数频率值的噪声或信号都能在电源系统中找到低 阻抗回流路径,但是对于那些频率值接近反谐振点的,由于电源系统表现出的高阻抗,使得 这部分噪声或信号能无法在电源分配系统中找到回流路径,最终会从 PCB 上发射出去 (空气也是一种介质,波阻抗只有几百欧姆) ,从而在反谐振频率点处产生严重的 EMI 问题。因此,并联电容去耦的电源分配系统一个重要的问题就是:合理的选择电容,尽可能 的压低反谐振点处的阻抗。
8.5 ESR 对反谐振(Anti-Resonance)的影响
Anti-Resonance 给电源去耦带来麻烦,但幸运的是,实际情况不会图 12 显示的那么糟 糕。实际电容除了 LC 之外,还存在等效串联电感 ESR,因此,反谐振点处的阻抗也不会是 无限大的。实际上,可以通过计算得到反谐振点处的阻抗为
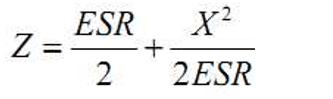
其中,X 为反谐振点处单个电容的阻抗虚部(均相等) 。现代工艺生产的贴片电容,等效串联阻抗很低,因此就有办法控制电容并联去耦时反谐振点处的阻抗。等效串联电感 ESR 使 整个电源分配系统的阻抗特性趋于平坦。
8.6 怎样合理选择电容组合
前面我们提到过,瞬态电流的变化相当于阶跃信号,具有很宽的频谱。因而,要对这一 电流需求补偿,就必须在很宽的频率范围内提供足够低的电源阻抗。但是,不同电容的有效 频率范围不同,这和电容的谐振频率有关(严格来说应该是安装后的谐振频率) ,有效频 率范围(电容能提供足够低阻抗的频率范围)是谐振点附近一小段频率。因此要在很宽的频 率范围内提供足够低的电源阻抗,就需要很多不同电容的组合。
你可能会说,只用一个容值,只要并联电容数足够多,也能达到同样低的阻抗。的确 如此,但是在实际应用中你可以算一下,多数时候,所需要的电容数很大。真要这样做的 话,可能你的电路板上密密麻麻的全是电容。既不专业,也没必要。
选择电容组合,要考虑的问题很多,比如选什么封装、什么材质、多大的容值、容值的 间隔多大、主时钟频率及其各次谐波频率是多少、信号上升时间等等,这需要根据具体的设 计来专门设计。
通常,用钽电容或电解电容来进行板级低频段去耦。电容的计算方法前面讲过了,需 要提醒一点的是,最好用几个或多个电容并联以小等效串联电感。这两种电容的 Q 值很 低,频率选择性不强,非常适合板级滤波。
高频小电容的选择有些麻烦,需要分频段计算。可以把需要去耦的频率范围分成几段, 一段单独计算,用多个相同容值电容并联达到阻抗要求,不同频段选择的不同的电容值。但这种方法中,频率段的划分要根据计算的结果不断调整。
一般划分 3 到 4 个频段就可以了,这样需要 3 到 4 个容值等级。实际上,选择的容 值等级越多,阻抗特性越平坦,但是没必要用非常多的容值等级,阻抗的平坦当然好,但是 我们的最终目标是总阻抗小于目标阻抗,只要能满足这个要求就行。
在某个等级中到底选择那个容值,还要看系统时钟频率。前面讲过,电容的并联存在反 谐振,设计时要注意,尽不要让时钟频率的各次谐波落在反谐振频率附近。比如在零点几 微法等级上选择 0.47、0.22、0.1 还是其他值,要计算以下安装后的谐振频率再来定。
还有一点要注意,容值的等级不要超过 10 倍。比如你可以选类似 0.1、0.01 、0.001 这样的组合。因为这样可以有效控制反谐振点阻抗的幅度, 间隔太大, 会使反谐振点阻 抗很大。
当然这不是绝对的,最好用软件看一下,最终目标是反谐振点阻抗能满足要求。
高频小电容的选择,要想得到最优组合,是一个反复迭代寻找最优解的过程。最好的办 法就是先粗略计算一下大致的组合,然后用电源完整性仿真软件做仿真,再做局部调整,能 满足目标阻抗要求即可,这样直观方便,而且控制反谐振点比较容易。而且可以把电源平面 的电容也加进来,联合设计。
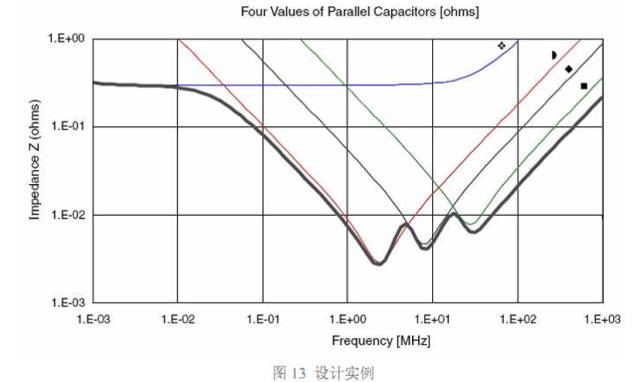
图 13 是一个电容组合的例子。这个组合中使用的电容为:2 个 680uF 钽电容, 7 个 2.2uF 陶瓷电容(0805 封装) ,13 个 0.22uF 陶瓷电容(0603 封装) ,26 个 0.022uF 陶 瓷电容(0402 封装) 。图中,上部平坦的曲线是 680uF 电容的阻抗曲线,其他三个容值的 曲线为图中的三个 V 字型曲线,从左到右一次为 2.2uF、0.22uF、0.022uF。总的阻抗曲线 为图中底部的粗包络线。
这个组合实现了在 500kHz 到 150MHz 范围内保持电源阻抗在 33 毫欧以下。到 500MHz 频率点处,阻抗上升到 110 毫欧。从图中可见,反谐振点的阻抗控制得很低。
小电容的介质一般常规设计中都选则陶瓷电容。NP0 介质电容的 ESR 要低得多,对于 有更严格阻抗控制的局部可以使用,但是注意这种电容的 Q 值很高,可能引起严重的高频 振铃,使用时要注意。
封装的选择,只要加工能力允许,当然越小越好,这样可以得到更低的 ESL,也可以留 出更多的布线空间。但不同封装,电容谐振频率点不同,容值范围也不同,可能影响到最终 的电容数。因此,电容封装尺寸、容值要联合考虑。总之最终目标是,用最少的电容达到 目标阻抗要求,轻安装和布线的压力。
8.7 电容的去耦半径
电容去耦的一个重要问题是电容的去耦半径。大多数资料中都会提到电容摆放要尽靠 近芯片,多数资料都是从小回路电感的角度来谈这个摆放距离问题。确实,小电感是一 个重要原因,但是还有一个重要的原因大多数资料都没有提及,那就是电容去耦半径问题。
如果电容摆放离芯片过远,超出了它的去耦半径,电容将失去它的去耦的作用。
理解去耦半径最好的办法就是考察噪声源和电容补偿电流之间的相位关系。当芯片对电 流的需求发生变化时,会在电源平面的一个很小的局部区域内产生电压扰动,电容要补偿这 一电流(或电压),就必须先感知到这个电压扰动。信号在介质中传播需要一定的时间,因 此从发生局部电压扰动到电容感知到这一扰动之间有一个时间延迟。同样,电容的补偿电流 到达扰动区也需要一个延迟。因此必然造成噪声源和电容补偿电流之间的相位上的不一致。特定的电容,对与它自谐振频率相同的噪声补偿效果最好,我们以这个频率来衡这种相位 关系。设自谐振频率为 f,对应波长为λ,补偿电流表达式可写为:
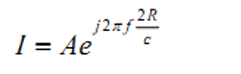
其中,A 是电流幅度,R 为需要补偿的区域到电容的距离,C 为信号传播速度。
当扰动区到电容的距离达到λ/4 时,补偿电流的相位为π ,和噪声源相位刚好差 180 度,即完全反相。此时补偿电流不再起作用,去耦作用失效,补偿的能无法及时送达。为 了能有效传递补偿能,应使噪声源和补偿电流的相位差尽可能的小,最好是同相位的。距 离越近,相位差越小,补偿能传递越多,如果距离为 0,则补偿能百分之百传递到扰动 区。这就要求噪声源距离电容尽可能的近,要远小于λ/4 。实际应用中,这一距离最好控 制在λ/40~λ/50 之间,这是一个验数据。
例如:0.001uF 陶瓷电容,如果安装到电路板上后总的寄生电感为 1.6nH,那么其安装 后的谐振频率为 125.8MHz,谐振周期为 7.95ps。假设信号在电路板上的传播速度为 166ps/inch,则波长为 47.9 英寸。电容去耦半径为 47.9/50=0.958 英寸,大约等于 2.4 厘 米。
本例中的电容只能对它周围 2.4 厘米范围内的电源噪声进行补偿,即它的去耦半径 2.4 厘米。不同的电容,谐振频率不同,去耦半径也不同。对于大电容,因为其谐振频率很低, 对应的波长非常长,因而去耦半径很大,这也是为什么我们不太关注大电容在电路板上放置 位置的原因。对于小电容,因去耦半径很小,应尽可能的靠近需要去耦的芯片,这正是大多 数资料上都会反复强调的,小电容要尽可能近的靠近芯片放置。
8.8 电容的安装方法
电容的摆放
对于电容的安装,首先要提到的就是安装距离。容值最小的电容,有最高的谐振频率, 去耦半径最小,因此放在最靠近芯片的位置。容值稍大些的可以距离稍远,最外层放置容值 最大的。但是,所有对该芯片去耦的电容都尽靠近芯片。下面的图 14 就是一个摆放位置 的例子。本例中的电容等级大致遵循 10 倍等级关系。
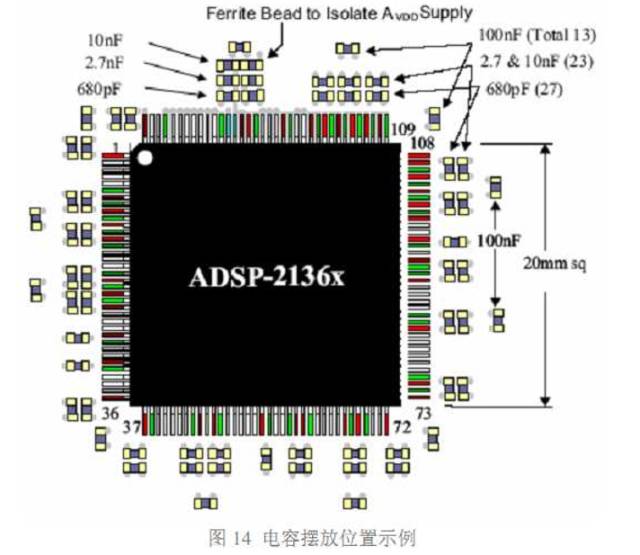
还有一点要注意,在放置时, 最好均匀分布在芯片的四周,对一个容值等级都要这 样。通常芯片在设计的时候就考虑到了电源和地引脚的排列位置,一般都是均匀分布在芯片 的四个边上的。因此,电压扰动在芯片的四周都存在,去耦也必须对整个芯片所在区域均 匀去耦。如果把上图中的 680pF 电容都放在芯片的上部,由于存在去耦半径问题,那么就 不能对芯片下部的电压扰动很好的去耦。
电容的安装
在安装电容时,要从焊盘拉出一小段引出线,然后通过过孔和电源平面连接,接地端也 同样。这样流电容的电流回路为:电源平面->过孔->引出线->焊盘->电容->焊盘->引出>过 孔->地平面,图 15 直观的显示了电流的回流路径。
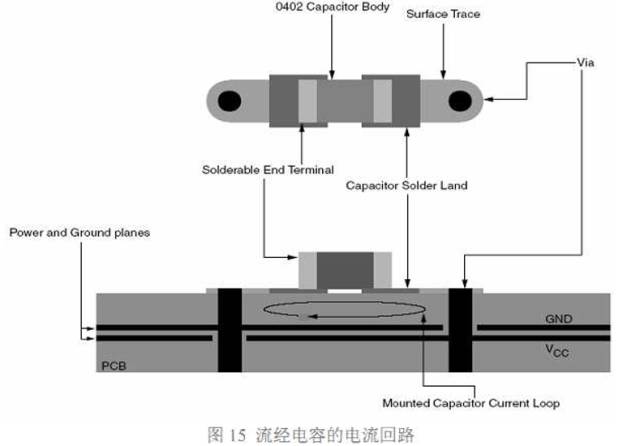
放置过孔的基本原则就是让这一环路面积最小,进而使总的寄生电感最小。图 16 显示 了几种过孔放置方法。
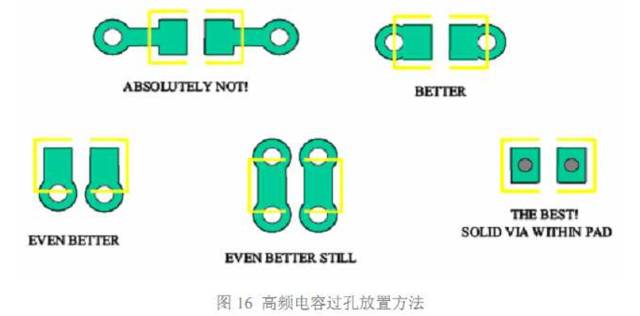
第一种方法从焊盘引出很长的引出线然后连接过孔,这会引入很大的寄生电感,一定要 避免这样做,这时最糟糕的安装方式。
第二种方法在焊盘的两个端点紧邻焊盘打孔,比第一种方法路面积小得多,寄生电感也 较小,可以接受。
第三种在焊盘侧面打孔,进一步小了回路面积,寄生电感比第二种更小,是比较好的 方法。
第四种在焊盘两侧都打孔,和第三种方法相比,相当于电容一端都是通过过孔的并联接入电源平面和地平面,比第三种寄生电感更小,只要空间允许,尽用这种方法。
最后一种方法在焊盘上直接打孔,寄生电感最小,但是焊接是可能会出现问题,是否使 用要看加工能力和方式。
推荐使用第三种和第四种方法。
需要强调一点:有些工程师为了节省空间,有时让多个电容使用公共过孔。任何情况下都不 要这样做。最好想办法优化电容组合的设计,少电容数。
由于印制线越宽,电感越小,从焊盘到过孔的引出线尽加宽,如果可能,尽和焊盘 宽度相同。这样即使是 0402 封装的电容,你也可以使用 20mil 宽的引出线。引出线和过 孔安装如图 17 所示,注意图中的各种尺寸。
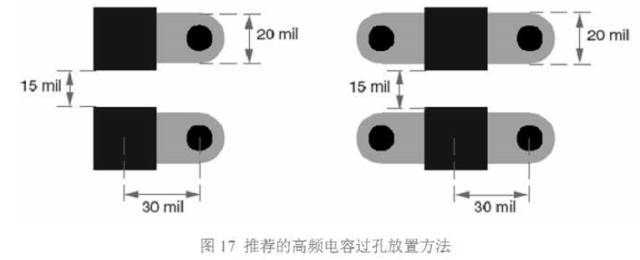
对于大尺寸的电容,比如板级滤波所用的钽电容,推荐用图 18 中的安装方法。

9 结束语
电源系统去耦设计要把引脚去耦和电源平面去耦结合使用已达到最优设计。时钟、 PLL、 DLL 等去耦设计要使用引脚去耦,必要时还要加滤波网络,模拟电源部分还要使用磁珠等进 行滤波。针对具体应用选择退耦电容的方法也很流行,如在电路板上发现某个频率的干扰较 大,就要专门针对这一频率选择合适的电容,改进系统设计。总之,电源系统的设计和具体 应用密切相关,不存在放之四海皆准的具体方案。关键是掌握基本的设计方法,具体情况具 体分析,才能很好的解决电源去耦问题。
原文标题:电源完整性设计的8大总结[20220506]
文章出处:【微信公众号:电磁兼容EMC】欢迎添加关注!文章转载请注明出处。
审核编辑:汤梓红
-
芯片
+关注
关注
457文章
51345浏览量
428244 -
晶体管
+关注
关注
77文章
9796浏览量
139067 -
电源噪声
+关注
关注
3文章
152浏览量
17535
原文标题:电源完整性设计的8大总结[20220506]
文章出处:【微信号:EMC_EMI,微信公众号:电磁兼容EMC】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
信号完整性为什么写电源完整性?
电源完整性基础知识
电源完整性基础知识





 电源完整性设计基础知识
电源完整性设计基础知识












评论