最大子序和，贪心解法

53. 最大子序和

力扣题目链接：https://leetcode-cn.com/problems/maximum-subarray

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例: 输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释:连续子数组[4,-1,2,1] 的和最大，为 6。

暴力解法

暴力解法的思路，第一层for 就是设置起始位置，第二层for循环遍历数组寻找最大值

时间复杂度：O(n^2) 空间复杂度：O(1)

classSolution{
public:
intmaxSubArray(vector<int>&nums){
intresult=INT32_MIN;
intcount=0;
for(inti=0;i< nums.size(); i++) { //设置起始位置
count=0;
for(intj=i;j< nums.size(); j++) { //每次从起始位置i开始遍历寻找最大值
count+=nums[j];
result=count>result?count:result;
}
}
returnresult;
}
};

以上暴力的解法C++勉强可以过，其他语言就不确定了。

贪心解法

贪心贪的是哪里呢？

如果 -2 1 在一起，计算起点的时候，一定是从1开始计算，因为负数只会拉低总和，这就是贪心贪的地方！

局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。

全局最优：选取最大“连续和”

局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。

从代码角度上来讲：遍历nums，从头开始用count累积，如果count一旦加上nums[i]变为负数，那么就应该从nums[i+1]开始从0累积count了，因为已经变为负数的count，只会拖累总和。

这相当于是暴力解法中的不断调整最大子序和区间的起始位置。

那有同学问了，区间终止位置不用调整么？如何才能得到最大“连续和”呢？

区间的终止位置，其实就是如果count取到最大值了，及时记录下来了。例如如下代码：

if(count>result)result=count;

这样相当于是用result记录最大子序和区间和（变相的算是调整了终止位置）。

如动画所示：

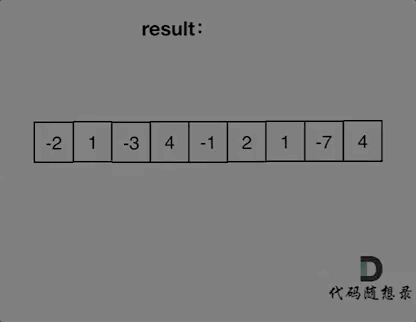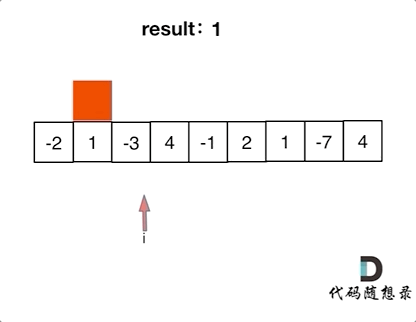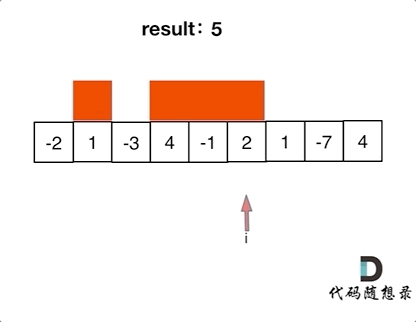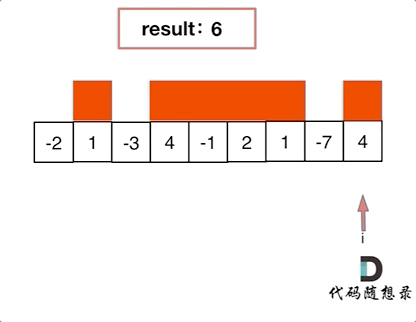53.最大子序和

红色的起始位置就是贪心每次取count为正数的时候，开始一个区间的统计。

那么不难写出如下C++代码（关键地方已经注释）

classSolution{
public:
intmaxSubArray(vector<int>&nums){
intresult=INT32_MIN;
intcount=0;
for(inti=0;i< nums.size(); i++) {
            count += nums[i];
            if(count>result){//取区间累计的最大值（相当于不断确定最大子序终止位置）
result=count;
}
if(count<= 0)count=0;//相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
}
returnresult;
}
};

时间复杂度：O(n) 空间复杂度：O(1)

当然题目没有说如果数组为空，应该返回什么，所以数组为空的话返回啥都可以了。

不少同学认为 如果输入用例都是-1，或者 都是负数，这个贪心算法跑出来的结果是0， 这是又一次证明脑洞模拟不靠谱的经典案例，建议大家把代码运行一下试一试，就知道了，也会理解 为什么 result 要初始化为最小负数了。

动态规划

当然本题还可以用动态规划来做，当前「代码随想录」主要讲解贪心系列，后续到动态规划系列的时候会详细讲解本题的dp方法。

那么先给出我的dp代码如下，有时间的录友可以提前做一做：

classSolution{
public:
intmaxSubArray(vector<int>&nums){
if(nums.size()==0)return0;
vector<int>dp(nums.size(),0);//dp[i]表示包括i之前的最大连续子序列和
dp[0]=nums[0];
intresult=dp[0];
for(inti=1;i< nums.size(); i++) {
            dp[i] = max(dp[i - 1]+nums[i],nums[i]);//状态转移公式
if(dp[i]>result)result=dp[i];//result保存dp[i]的最大值
}
returnresult;
}
};

时间复杂度：O(n) 空间复杂度：O(n)

总结

本题的贪心思路其实并不好想，这也进一步验证了，别看贪心理论很直白，有时候看似是常识，但贪心的题目一点都不简单！

后续将介绍的贪心题目都挺难的，哈哈，所以贪心很有意思，别小看贪心！

其他语言版本

Java

classSolution{
publicintmaxSubArray(int[]nums){
if(nums.length==1){
returnnums[0];
}
intsum=Integer.MIN_VALUE;
intcount=0;
for(inti=0;i< nums.length; i++){
            count += nums[i];
            sum = Math.max(sum, count); //取区间累计的最大值（相当于不断确定最大子序终止位置）
if(count<= 0){
count=0;//相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
}
}
returnsum;
}
}

//DP方法
classSolution{
publicintmaxSubArray(int[]nums){
intans=Integer.MIN_VALUE;
int[]dp=newint[nums.length];
dp[0]=nums[0];
ans=dp[0];

for(inti=1;i< nums.length; i++){
            dp[i] = Math.max(dp[i-1]+nums[i],nums[i]);
ans=Math.max(dp[i],ans);
}

returnans;
}
}

Python

classSolution:
defmaxSubArray(self,nums:List[int])->int:
result=-float('inf')
count=0
foriinrange(len(nums)):
count+=nums[i]
ifcount>result:
result=count
ifcount<= 0:
count=0
returnresult

Go

funcmaxSubArray(nums[]int)int{
maxSum:=nums[0]
fori:=1;i< len(nums);i++{
ifnums[i]+nums[i-1]>nums[i]{
nums[i]+=nums[i-1]
}
ifnums[i]>maxSum{
maxSum=nums[i]
}
}
returnmaxSum
}

--- EOF ---

审核编辑 ：李倩