关于彩色图像高斯反向投影基于OpenCV的C++代码

彩色图像高斯反向投影

一：介绍

图像反向投影的最终目的是获取ROI然后实现对ROI区域的标注、识别、测量等图像处理与分析，是计算机视觉与人工智能的常见方法之一。图像反向投影通常是彩色图像投影效果会比灰度图像效果要好，原因在于彩色图像带有更多对象细节信息，在反向投影的时候更加容易判断、而转为灰度图像会导致这些细节信息丢失、从而导致分割失败。最常见的是基于图像直方图特征的反向投影。我们这里介绍一种跟直方图反向投影不一样的彩色图像反向投影方法，通过基于高斯的概率分布公式（PDF）估算，反向投影得到对象区域，该方法也可以看做最简单的图像分割方法。缺点是对象颜色光照改变和尺度改变不具备不变性特征。所以需要在光照度稳定情况下成像采集图像数据。 在这种情况下使用的高斯概率密度公式为：

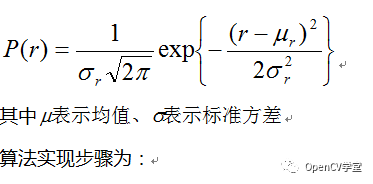
1. 输入模型M，对M的每个像素点（R,G,B）计算I=R+G+B r=R/I, g=G/I, b=B/I

2. 根据得到权重比例值，计算得到对应的均值 与标准方差

3. 对输入图像的每个像素点计算根据高斯公式计算P(r)与P(g)的乘积

4. 归一化之后输出结果，即为最终基于高斯PDF的反向投影图像

二：算法步骤与代码实现

1. 首先加载模型图像与测试图像

2. 根据模型图像计算得到每个通道对应的均值与标准方差参数

3. 根据参数方差计算每个像素点的PDF值

4. 归一化概率分布图像-即为反向投影图像，显示

5. 根据Mask得到最终颜色模型对象分割

完整的基于OpenCV的C++代码如下：

1. #include

2. #include

3. #include

5. using namespace cv;

6. using namespace std;

8. int main(int argc, char** argv) {

9. // 加载模型图像与测试图像

10. Mat src = imread("D:/gloomyfish/gc_test.png");

11. Mat model = imread("D:/gloomyfish/gm.png");

12. if (src.empty() || model.empty()) {

13. printf("could not load image... ");

14. return -1;

15. }

16. imshow("input image", src);

18. // 对每个通道 计算高斯PDF的参数

19. // 有一个通道不计算，是因为它可以通过1-r-g得到

20. // 无需再计算

21. Mat R = Mat::zeros(model.size(), CV_32FC1);

22. Mat G = Mat::zeros(model.size(), CV_32FC1);

23. int r = 0, g = 0, b = 0;

24. float sum = 0;

25. for (int row = 0; row < model.rows; row++) {

26. uchar* current = model.ptr(row);

27. for (int col = 0; col < model.cols; col++) {

28. b = *current++;

29. g = *current++;

30. r = *current++;

31. sum = b + g + r;

32. R.at(row, col) = r / sum;

33. G.at(row, col) = g / sum;

34. }

35. }

37. // 计算均值与标准方差

38. Mat mean, stddev;

39. double mr, devr;

40. double mg, devg;

41. meanStdDev(R, mean, stddev);

42. mr = mean.at(0, 0);

43. devr = mean.at(0, 0);

45. meanStdDev(G, mean, stddev);

46. mg = mean.at(0, 0);

47. devg = mean.at(0, 0);

49. int width = src.cols;

50. int height = src.rows;

52. // 反向投影

53. float pr = 0, pg = 0;

54. Mat result = Mat::zeros(src.size(), CV_32FC1);

55. for (int row = 0; row < height; row++) {

56. uchar* currentRow = src.ptr(row);

57. for (int col = 0; col < width; col++) {

58. b = *currentRow++;

59. g = *currentRow++;

60. r = *currentRow++;

61. sum = b + g + r;

62. float red = r / sum;

63. float green = g / sum;

64. pr = (1 / (devr*sqrt(2 * CV_PI)))*exp(-(pow((red - mr), 2)) / (2 * pow(devr, 2)));

65. pg = (1 / (devg*sqrt(2 * CV_PI)))*exp(-(pow((green - mg),2)) / (2 * pow(devg, 2)));

66. sum = pr*pg;

67. result.at(row, col) = sum;

68. }

69. }

71. // 归一化显示高斯反向投影

72. Mat img(src.size(), CV_8UC1);

73. normalize(result, result, 0, 255, NORM_MINMAX);

74. result.convertTo(img, CV_8U);

75. Mat segmentation;

76. src.copyTo(segmentation, img);

78. // 显示

79. imshow("backprojection demo", img);

80. imshow("segmentation demo", segmentation);

82. waitKey(0);

83. return 0;

84. }

三：测试图像与效果演示

蓝色矩形框为模型，整个图像为测试图像

反向投影结果

分割提取结果

四：总结

大家看了这个例子总是有点怪怪的，总会想起点什么，如果你能想起点什么的话就是GMM，高斯混合模型，高斯混合模型正是在此基础上进一步演化而来。

审核编辑 ：李倩