形式化方法背后的动因和关键技术及行业应用

系列简介：形式化方法在计算机和软件工程学科中作为一个学科分支，正在越来越多地进入工业界诸多实践领域。以DO-333适航标准为代表的工业标准，亦对软件开发过程明确提出了采用形式化方法的要求。为此，结合上海控安形式化方法技术团队历年来在航空、航天和轨交等领域的成功应用经验，本专题将围绕“形式化方法”特别是形式化方法的工程化应用，组织一系列文章，探讨形式化方法背后的动因和关键技术及行业应用。

01

传统软件工程面临的困难

自从1968年“软件工程”这个学科概念提出以来，软件工程的研究和实践有效地解决了软件的质量和研制效率问题。但是传统软件工程中存在的大量依赖人工的活动和主观性判断等过程和技术，给软件带来了日趋明显的可信问题。我们以工业领域最常见的 “V”字模型为例探讨传统软件工程中的一些局限性。

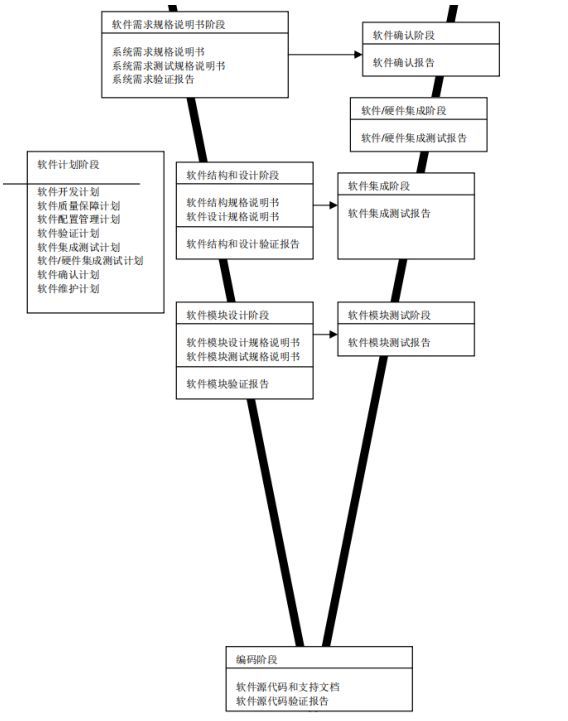
图1 常见于工业标准的V字模型

按照V模型的软件开发过程，我们可以看到，即使是工业界较为推崇的V模型，其描述的软件研制过程仍然存在明显的局限性和风险：

（1）软件研制过程中文档的准确性

软件需求普遍以自然语言来撰写需求文档。由于自然语言天然的二义性和模糊性，造成文档难以精确描述软件预期功能和性能。设计文档采用图形化描述，往往缺乏严格的语法和语义。此类中间产物的缺陷往往持续传递至代码和测试阶段，部分深层次问题几乎始终无法探测。

（2）软件研制过程对主观活动的依赖性

软件研制过程中，各阶段的转换及产物之间的一致性，严重依赖人工判断。例如设计文档是否与需求文档中功能和行为描述一致，往往通过人工审查和比对来进行。

（3）软件研制过程的严谨性

软件研制过程中的中间产物，缺乏严格分析手段。例如，自然语言撰写的需求文档难以被严格分析。设计文档刻画的系统架构，通过简单的仿真进行而缺少对系统行为深层次的验证，例如死锁等安全隐患难以揭示。

尽管业界和学术界在软件工程理论和实践中取得了丰硕成果，软件质量问题始终是行业的一大难题。2017年11月28日 俄罗斯“联盟-2.1B”火箭发射失败，软件错误导致19颗卫星烧毁。波音737MAX机型的控制软件对人机控制优先级的错误设计，导致2018年和2019年两次恶性坠机事件。

随着软件产品对社会生产生活的重要性日趋上升，如何改善并发展现有的软件工程方法，使其能对软件的安全可信提供更为可靠的保障，成为了工业界和学术界普遍关心的问题。在此背景下，形式化方法以其严谨的数学理论基础和不断发展的技术手段，被视为一种极有潜力的解决方案。

02

形式化方法发展历史

在20世纪60年代，Floyd、Hoare和Manna等试图用数学方法来证明程序的正确性并发展成了各种程序验证方法。随后软件工程界认识到了数学方法的巨大潜力，形式化方法一词开始传播开来。1969-1972年之间， C.A.R Hoare撰写了"计算机编程的公理基础"和"数据表示的正确性证明"两篇开创性的论文，并提出了规格说明的概念。

在形式语义与形式化建模以及形式化规约的基础上，将计算机系统的分析与验证问题转化为逻辑推理问题或者形式模型的判断问题，用定理证明工具/求解器或者某个形式模型的原型工具来进行验证。交互式定理证明需要用户与计算机相互协助来进行形式化证明。最常用的证明辅助是Coq和Isabelle，均有在空客等航空领域项目中成功应用的记录。

模型检验的基本思想是通过遍历系统的状态空间以验证系统模型是否满足给定的关键性质，并在不满足性质时给出具体反例路径。例如在航空等安全攸关领域，常用于分析系统是否满足给定的功能需求或安全性质。较有代表性的工具包括SPIN、UPPAAL和 PRISM等，在工业界尤其是在硬件系统的分析与验证上取得了很大的成功。

关于形式化验证的定理证明、模型检测等方法，特别是在轨交、航空、航天和汽车电子及工业控制等行业的成功应用以及相关工具的研发，我们将在后续的文章中作更为深入和系统化的探讨。

03

形式化方法的简介

形式化方法(Formal Methods)是一种基于数学的开发软件系统的方法学，它提供了一种数学化的框架，在此框架之下开发者可以通过定义系统和验证系统的方式，以系统化的手段逐步开发软件。

从广义上讲，形式化方法是指将离散数学的方法用于解决软件工程领域的问题，主要包括建立精确的数学模型以及对模型的分析活动。狭义地讲，形式化方法是运用形式化语言，进行形式化的规格描述、模型推理和验证的方法。

通常来说，形式化方法强调了对软件预期功能和行为的“描述（specify）”和“验证（verify）”。描述强调通过精确的形式化语言刻画软件，验证则强调通过数学手段严格地分析软件是否是一致的、是否满足给定的性质等。由此我们可以认为，形式化方法包含两项目主要分支，形式化规格说明技术和形式化验证技术。这两种技术都是基于数学基础，例如集合论、逻辑和代数理论等，如图3所示。

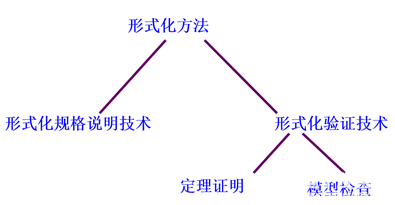
图3 形式方法的构成

形式化规格说明技术可以视为一种对软件形式化建模的过程。一般来说，形式化建模需要有特定的形式化语言，此类语言基本上可以分为下述类型：

基于模型的语言

此类形式化语言基本思想是利用一些已知特性的数学抽象来为目标软件系统的状态特征和行为特征构造模型，包括域、元组、集合等。Z、VDM，B等都是面向模型的语言。

代数方法语言

代数方法仅使用带有等词的一阶逻辑的表示，而不引入通常的数学对象。常见的代数方法有Larch等。

进程代数语言

进程代数提供了描述并发系统所需的并行复合，选择，顺序复合等语句。并可通过等式推理（equatioanl reasoning）的方法来验证系统满足某些性质。常见的进程代数语言有CSP等。

形式化验证就是基于已建立的形式化规格说明的基础上，对所描述系统的相关性质进行分析以评判系统是否满足期望的性质，尽可能地发现其中的不一致性、模糊性、不完备性等错误。形式化验证的主要技术包括定理和模型检测。

定理证明技术是形式方法的核心，定理证明系统是由一个形式语言和推理机制构成的形式系统。推理机制由公理和推理规则组成。通常的定理证明过程需要工具的支持。使用定理证明技术，我们可以对用户期望的或系统应具有的性质进行证明，以消除规格说明中的模糊性、不一致性、不安全性等。

模型检测是一种自动验证系统正确性的方法。模型检测器的输入通常是一个系统的有限状态模型以及一组用时态逻辑表达的系统预期的性质。通过搜索有限状态模型所有的可能事件序列来判定系统性质是否得到满足。由于系统的模型是有限的，因此系统状态空间的搜索能终止。假如系统的性质成立，则模型检测器输出一个肯定结果。如果性质不满足，则系统输出一个以状态序列表示的反例。

一个最简单的例子：

假如在一个飞行器中有一款控制软件，需要完成飞行控制行为。其中某条功能为“求一个给定正数的非负数平方根”。我们用形式化语言Z来描述这条软件功能，如图4所示。

图4 模式SquareRootSpec

其中的E形框称为模式框架 (Schema Box)，可以近似看作一个“操作”，顶部的标识符 SquareRootSpec 称为模式名称，中间水平线起分隔作用，水平线上部称为声明部分，水平线下面是谓词部分，由若干个谓词组成，这些谓词通过联结词“∧”形成一个完整的谓词。该例中将radicand? 和squareroot! 都声明为实数类型，分别为输入变量和输出变量。

从这个例子可以看出，形式化语言刻画软件功能时，更多地是通过一种数学上的“抽象”来精确描述待开发的软件。在这个例子里，求平方根的细节过程并不是重点要刻画的对象，而是通过“squareroot!2= radicand?”这个等式来表达一种“关系”，即“待求的非负数平方根，其平方一定等于被开方数”。对于软件来说，这种关系是必然的、唯一的，而代码实现求解的方式则是多样的。

上面这个例子里，若我们把Z语言撰写的模式看作是一个“软件需求的形式化描述”，那么我们就可以对这个形式化的需求做进一步的分析验证。假定，我们想表达的是“求一个给定正数的非负数平方根”，但是写需求的人员，误将要输出的非负数平方根变量squareroot!写成了负数平方根，即整个谓词部分变成了“radicand?≥0 ∧ squareroot! 2= radicand? ∧squareroot!<0”。此时我们该如何发现这个缺陷呢？

假定需求分析过程中，我们还有一位需求检查者。检查者可以通过数学证明的方式来发现这个缺陷。例如，检查者可以在谓词表达式之后插入一个断言“squareroot! ≥0”。此时，谓词表达式应该满足这个断言。

通过数学证明的方式，显然可以发现，“radicand?≥0 ∧ squareroot! 2= radicand? ∧squareroot!<0”是无法推出“squareroot! ≥0”的，即原先撰写的谓词与给定的断言相矛盾。

上面的例子是一个非常简单的示例，仅用于说明最简单的形式化描述和分析过程。在我们后续的推文中，我们将陆续深入阐释形式化建模和形式化验证的相关技术以及其行业应用。

审核编辑：符乾江