HASH哈希游戏开发（技术方案）：开放寻址法详解

什么是哈希开放寻址法？

开放寻址法，就是当发生哈希冲突时，重新找到空闲的位置，然后插入元素。寻址方式有多种，常用的有线性寻址、二次方寻址、双重哈希寻址：

​线性寻址​，当需要插入元素的位置被占用时，顺序向后寻址，如果到数组最后也没找到一个空闲位置，则从数组开头寻址，直到找到一个空闲位置插入数据。线性寻址的每次寻址步长是1，寻址公式​​hash(key)+n​​（n是寻址的次数）。 ​二次方寻址​，就是线性寻址的总步长的二次方，即​​hash(key)+n^2​​。 ​双重哈希寻址​，顾名思义就是多次哈希直到找到一个不冲突的哈希值。

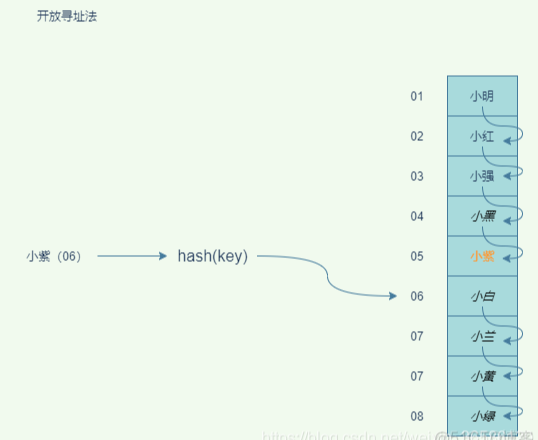
采用开放寻址法解决哈希冲突，又该如何查找元素和删除元素呢？

查找元素的过程和插入元素类似，用相同的寻址方式，寻址的同时比对key或者value是否相等，相等则认为元素存在，不相等则继续寻址，​如果探测到空闲位置依然没有找到则认为该元素不存在​。

删除有些特别，​不能单纯的把要删除的元素设置为空​，因为在查找元素的过程中探测到的空闲位置是删除元素的位置，就会使得查找元素的寻址算法失效，本来存在的元素误判定为不存在。该如何解决这个问题呢？

​只需要删除元素不是物理删除而是逻辑删除​。给删除的元素做上delete标记，当查询元素寻址时遇到delete标记的位置时不会停下来而是​继续向后探测​，但是在插入元素寻址遇到delete标记的位置就会把应该删除的元素替换掉。

三种寻址方式都有着明显的不足：

线性寻址，寻址的性能虽然元素个数的增多逐步下降，最坏时间复杂度是O(n)。 二次方寻址，寻址的次数比线性寻址较低了，但是会因为步长是二次方，所以需要较长的数组长度，内存利用率可能较低。 双重哈希寻址，多次哈希可能会浪费时间，需要优质的哈希函数做支撑。

而整个开放寻址法的不足也很明显：

插入、查找、删除都需要寻址。 数组中元素越多，空闲位置越少，哈希冲突越剧烈。所以装载因子不能太大，要及时扩容减小冲突，但是数组内存利用率较低。

看似开放寻址法有挺多问题，但是也有一些优点：

数据都存储在数组中，可以有效地利用 CPU 缓存加快查询速度。 而且，这种方法实现的哈希表，序列化也简单，不像链表还要考虑指针。

总结而得，当数据量比较小、装载因子小的时候，适合采用开放寻址法。这也是 Java 中​​ThreadLocal​​​内部类​​ThreadLocalMap​​使用开放寻址法解决散列冲突的原因。

审核编辑：符乾江