新冠大流行给世界带来了巨大的改变,全球科学家和研究人员在研制有效的疫苗。他们正在做的就是从广阔的样本空间中近似地收紧可能性范围,并尽力得到一些有效解。近似在我们的生活中发挥了重要作用。以在线食品配送为例,我们经常从网上订购食物,享受快速送达的服务。但你想过这些 app 后端运行的什么算法让快递员在更短时间内抵达目的地吗?答案是近似算法。这类问题就是「旅行商问题」。
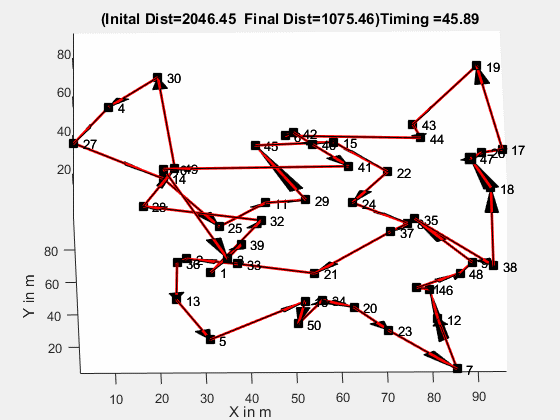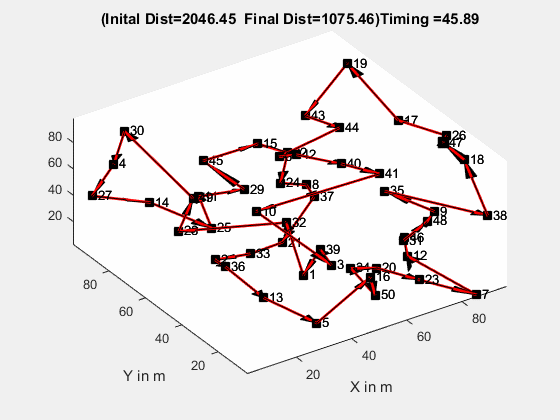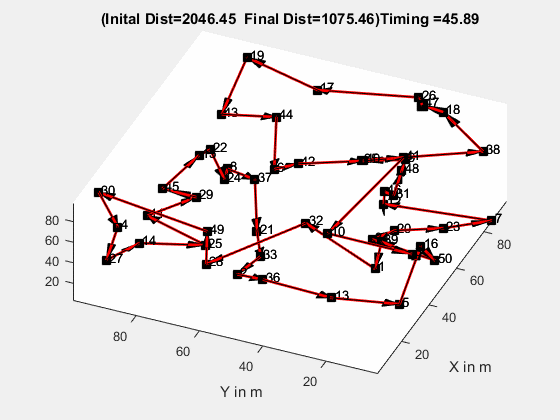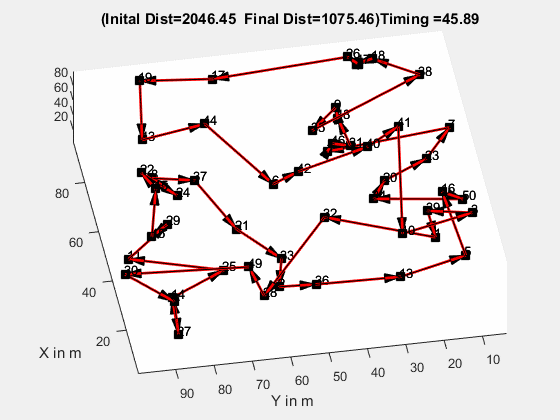
食品配送:旅行商问题的现实应用。本文将介绍近似算法及其对某些标准问题的适用性,以及哪些因素会影响到特定算法的选择。什么是近似算法?近似算法是一种处理优化问题 NP 完全性的方式,它无法确保最优解。近似算法的目标是在多项式时间内尽可能地接近最优值。它虽然无法给出精确最优解,但可以将问题收敛到最终解的近似值。其目标满足以下三个关键特性:
能够在多项式时间内高效运行;
能够给出最优解;
对于每个问题实例均有效。
背景数学表达式的评估常伴随常量、变量分析和方程的阶,可用于衡量近似的复杂度。此类评估将问题分解为 P 和 NP 难问题。P 问题和 NP 问题的策略P 问题是指可以在多项式时间内求解的问题。NP 表示不确定性多项式时间(nondeterministic polynomial time),NP 问题是指在多项式时间内近似验证答案的问题。但目前人们发现,很多此类问题需要指数时间才能求解。
P 和 NP 策略。真正的争论在于 P=NP 还是 P≠NP。之前的一些研究证明这两种都是对的。如果一个问题是多项式次方,则存在多个最优算法。因此,在 NP 完全问题中,存在两种方法找到近优解,然后选择最适合的算法。如果输入的大小比较小,则具备指数运行时间的算法可能会比较适合。其次,通过用近似算法替代确定性算法,我们仍然能够在多项式时间内找到近优解。近似算法的复杂度可以从输入大小和近似因子中推断出来。接下来,我们通过一些示例,深入探索这些算法如何应用到现实问题中。分区问题(Partition Problem)在计算机科学领域,该问题的定义是:给定多重正整数集 X,它可以被分割为两个元素之和相等的子集 X1 和 X2,即每个子集的数值之和与另一个子集相等。
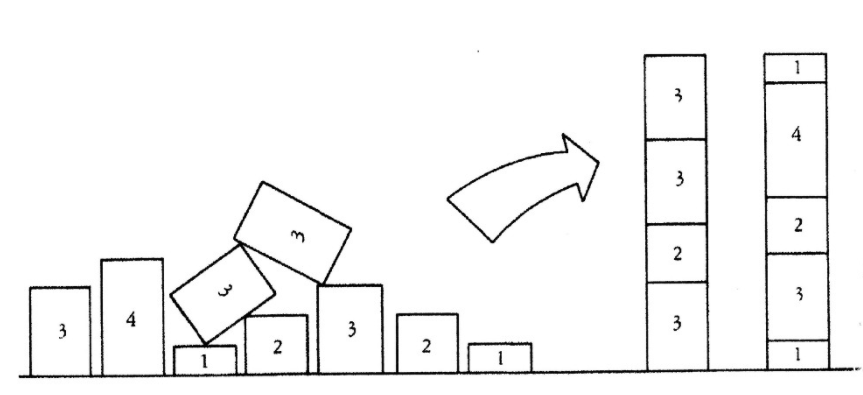
例如,X={3,4,1,3,3,2,3,2,1} 可以被分割为 X1={3,3,2,3} 和 X2={4,2,3,1,1},二者的数值之和都是 11。类似地,X={1,3,1,2,1,2} 可以被分成 X1={2,1,1,1} 和 X2={3,2},两个子集的数值之和都是 5。有趣的是,这不是唯一解。X1={1,3,1} 和 X2={2,1,2} 的数值之和也为 5,这表明存在多个可能的子集。这就是 NP 完全问题,存在伪多项式时间动态规划解,可获得该问题的近优解。方法和决定步骤现在,我们开始分析这个问题,把它分解成数个单独的标准问题。这里,我们想要找出多重集的元素之和相等的子集,那么该问题就可以分解成以下两个问题:
子集和问题:子集 X 的元素之和等于数字 W。
多路数字分割:给定整数参数 W,确定如何将 X 分割成 W 个等额子集。
近似算法如上所述,将分区问题分解为多路分割与子集和问题后,我们就可以考虑为这些问题而开发的算法,包括:贪婪数字分割(Greedy number Partitioning)该算法循环遍历所有数字,将每个数字分配给总和最小的子集。如果数字未以排序方式排列,则其运行时复杂度为 O(n),近似率约为 3/2。其 Python 伪代码如下:
def find_partition(numbers):"""Separate the available numbers into two eqal sum series.Args:numbers: collection of numbers, for example list of integers.Returns:Two lists of numbers."""X = []Y = []sum_X = 0sum_Y = 0for n in sorted(numbers, reverse=True):if sum_X < sum_Y:X.append(n)sum_X = sum_X + nelse:Y.append(n)sum_Y = sum_Y + nreturn (X, Y)
将数字排序,则运行时复杂度增加到 O(n logn),近似率增加到 7/6。如果数字在 [0,1] 范围内均匀分布,则近似率约为 1 + O(log logn/n)。
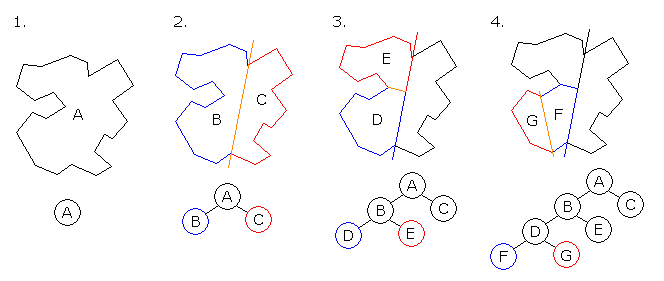
分区问题图示。上图用二叉树的形式展示所有分区。树的根部表示集合中的最大数,每一级对应输入数字,每个独立分支对应不同的子集。遍历这些集合需要深度优先遍历(depth-first traversal),所需的空间复杂度为 O(n),时间复杂度为 O(2^n)。适用性:该算法可以根据情况进行修改,以便改善运行时复杂度。每一级的首要目标是构建一个分支,将当前数字分配给总和最小的子集。首先通过贪婪数字分割找出总和,然后切换到优化,得到全多项式时间近似解。Karmarkar-Karp 算法Karmarkar-Karp 算法指以降序方式排列数字的最大差分方法,该方法将差值替换掉原来的数字不断放进集合中。其 Java 伪代码实现如下:
int karmarkarKarpPartition(int[] baseArr) {// create max heapPriorityQueue heap = new PriorityQueue(baseArr.length, REVERSE_INT_CMP);for (int value : baseArr) {heap.add(value);}while (heap.size() > 1) {int val1 = heap.poll();int val2 = heap.poll();heap.add(val1 - val2);}return heap.poll();}
该算法包含输入集 S 和参数 k。将 S 分割成 k 个子集,使这些子集中的数字总和相等,从而构建期望输出。该算法包含如下关键步骤:
以降序方式排列数字;
用差值替换掉原来的数字,直到只有一个数字;
采用回溯算法,完成分区。
适用性:该算法通过构建二叉树来假设分区。每一级表示一对数字,左侧的分支表示用差值替换数字,右侧的分支表示将差值放置在同一个子集中。该算法先通过最大差分求得解,然后继续寻找更好的近似解。它所需的空间复杂度为 O(n),但最糟糕的情况下所需的时间复杂度可能会达到 O(2^n)。装箱问题装箱问题有多种现实应用。例如,如何从根本上改善印度的垃圾管理系统。这个问题就可以通过装箱问题来解决,帮助当局决定 x 量的垃圾需要多少个垃圾箱。
在计算机科学领域中,该问题可用于多种内存管理技术。在该算法中,我们可以通过去除冗余和最小化空间浪费来包装不同形状和大小的对象。例如:给定一个包含 n 个项的集合,每个项的大小分别为 s1,s2,。.,sn (0《=si《=1, 1《=i《=n),如何将它们装进最少数量的箱子?经典方法:1. 邻近适应算法 (Next Fit):查看当前项是否适合当前箱子。如果适合,则将物品放置在箱子里,否则开启一个新的箱子。我们来看一个示例:项是 0.5, 0.7, 0.5, 0.2, 0.4, 0.2, 0.5, 0.1, 0.6,箱子大小均为 1。
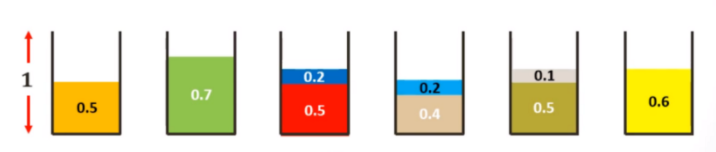
基于邻近适应算法的装箱解决方案(M = 箱子总数 = 6)。2. 最先匹配法 (First Fit):按顺序浏览箱子,在第一个箱中放置新的项,直到放不下再启用新的箱子。我们来看一个示例:项是 0.5, 0.7, 0.5, 0.2, 0.4, 0.2, 0.5, 0.1, 0.6,箱子的大小均为 1。
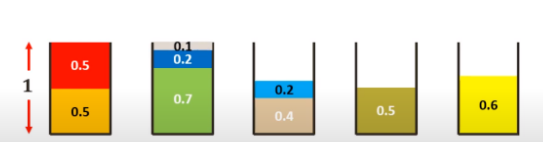
基于最先匹配法的装箱解决方案(M = 箱子总数 = 5)。3. 最优匹配法 (Best Fit):按顺序浏览箱子,将每一个新的项放在最适合的箱子里。如果不适合,则创建一个新的箱子。我们来看一个示例:项是 0.5, 0.7, 0.5, 0.2, 0.4, 0.2, 0.5, 0.1, 0.6,箱子的大小均为 1。
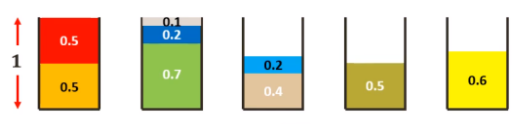
基于最优匹配法的装箱解决方案(M = 箱子总数 = 5)。该方法的输出与最先匹配法相同,但该方法的优点是实现速度比 FFD 快,即时间复杂度为 O(nlogn)。自然方法:如果我们提前知道所有项的大小,那么自然的解决方案就是首先按照从大到小排序,然后应用以下启发式方法:
最先匹配递减法
最优匹配递减法
假设有相同的示例 0.7, 0.6, 0.5, 0.5, 0.5, 0.4, 0.2, 0.2, 0.1,则排序为 0.7, 0.6, 0.5, 0.5, 0.5, 0.4, 0.2, 0.2, 0.1。
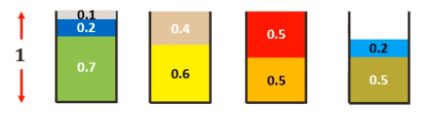
优化方法(M = 箱子总数 = 4)。
审核编辑:郭婷
-
计算机
+关注
关注
19文章
7500浏览量
88029 -
python
+关注
关注
56文章
4797浏览量
84727
原文标题:什么是近似算法?它适用于哪些问题?这篇文章给你答案
文章出处:【微信号:vision263com,微信公众号:新机器视觉】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
言必信电源滤波器的适用性:不仅仅局限于用电稳定且消耗小的器材

706-512B-010分体雷达液位计适用于哪些液体
回路电流法和节点电压法适用范围
如何保障光伏发电装置的安全性和适用性

热门研华工控机:除了研华工控610l,研华还有哪些产品适用性高?
论RISC-V的MCU中UART接口的重要性
M5_4芯接头便捷性怎么样

鸿蒙系统三防平板电脑突出的性能和环境的适用性
电子镇流器热保护器:优势和适用性分析
直线模组的适用性





 近似算法及对某些标准问题的适用性
近似算法及对某些标准问题的适用性












评论