教你如何利用傅里叶变换干漂亮的事

今天分享一篇关于傅立叶变换理解的文章，先来一张动图。

这篇文章可以说是介绍傅里叶变换最清晰通俗的，没有之一，直接把你当做小学生来讲，通过大量的动画不但告诉你傅里叶变换是什么，还告诉你傅里叶变换能干什么。

难能可贵的是，你可以通过手动绘制图案和拖动滑块来加深读傅里叶变换的理解。

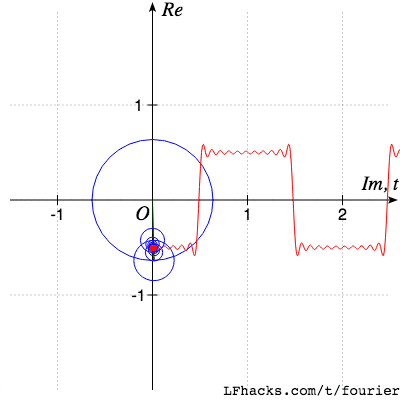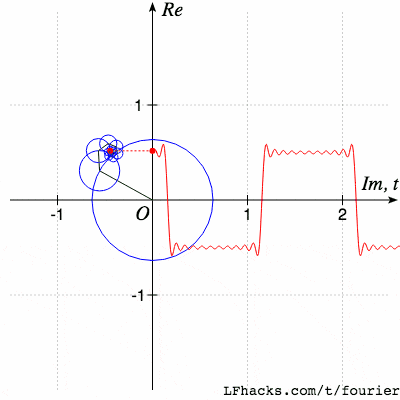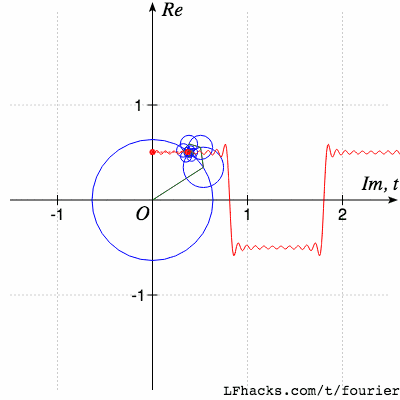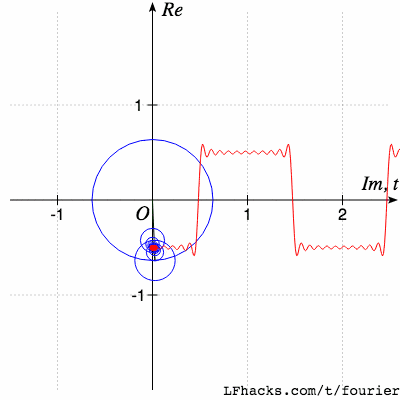
傅里叶变换是一种在各个领域都经常使用的数学工具。这个网站将为你介绍傅里叶变换能干什么，为什么傅里叶变换非常有用，以及你如何利用傅里叶变换干漂亮的事。就像下面这样：

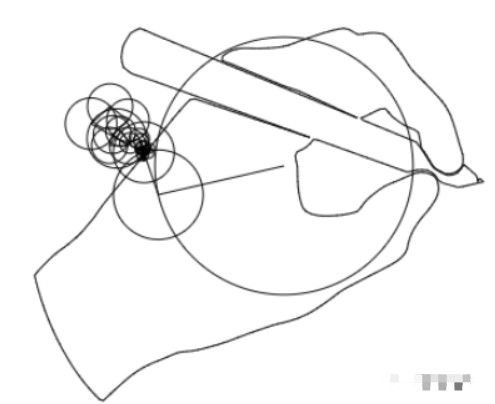
我将为你解释这个动画是如何工作的，沿途为你详细地解释傅里叶变换！ 这次旅途结束后，你将会掌握下面这些知识：

什么是傅里叶变换

傅里叶变换的一些实际用途

傅立叶变换的一些很酷的用法（虽然有些没有实际意义）

我们现在暂时不提那些复杂的数学公式。傅里叶背后的数学原理十分有趣，但最好还是先从它的实际应用开始，以及为什么要使用它。如果你想了解更多，下面提供了一些进一步的阅读建议！

一、傅里叶变换是什么

简而言之，傅里叶变换把一个输入信号分解成一堆正弦波的叠加。就像大多数数学方法一样，这个名字来自一个名叫傅立叶的人。

让我们从一些简单的例子开始，然后继续前进。首先，我们来看看什么是波 —— 波随着时间的推移，一直按照某一规律变化。 这是一个波的例子：

这个波可以分解为两个正弦波的叠加。也就是说，当我们将两个正弦波相加时，就会得到原来的波。

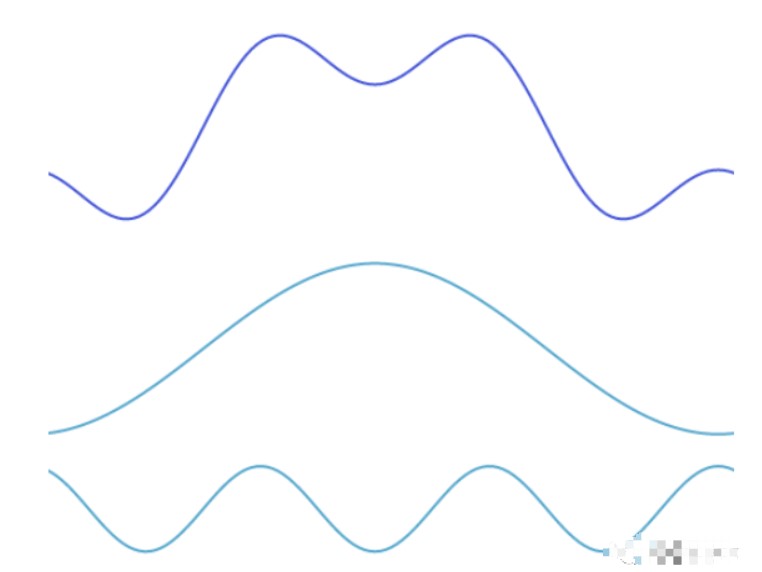
傅里叶变换可以让我们从一个复杂的波形里面，把构成这个波的单个正弦波分离出来。在这个例子中，你几乎可以通过“脑补”完成这一操作。

为什么？事实证明，现实世界中的许多事物间的互相交互，都是基于正弦波。我们通常将这种波的快慢的性质，称为波的频率。

最明显的例子就是声音 —— 当我们听到声音时，我们听不到那条波浪线，但我们听到构成声音的正弦波的不同频率。

能够在计算机上区分这两个音调，我们就可以了解一个人实际可以听到的内容。我们可以理解声音的高低，或弄清楚这个波包含了什么音符。

一些波看起来不像由正弦波构成，我们也可以用这个分解的过程来进行分析。 我们来看看这个家伙吧。这个波称为方波。

虽然看起来不太可能，但它确实也可以分解成正弦波。

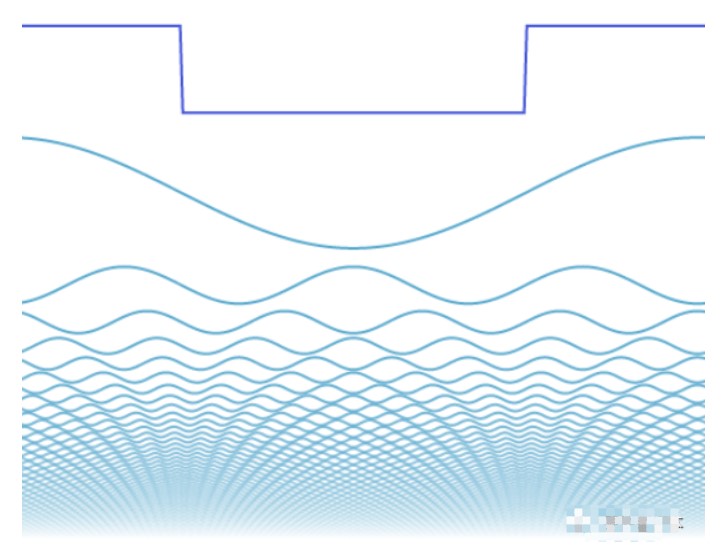
这次我们需要很多 —— 理论上是无限多的正弦波来完美地表达一个方波。随着我们加入越来越多的正弦波，叠加出的波形就越来越接近方波。

在视觉上，你会注意到前几个正弦波的叠加可以在结果中产生最大差异。滑块滑到一半时，就有一些方波的样子了，但它看起来摇摆不定。加上更多小的正弦波，组合出的波形看起来就平坦了。

当播放这个波形时，你会发现使用的正弦波少时，声音听起来更低沉一些。这是因为我们把高频率的成分去掉了。

这一过程可以用来处理任何有周期的波。试一试，画一个你喜欢的波形吧。

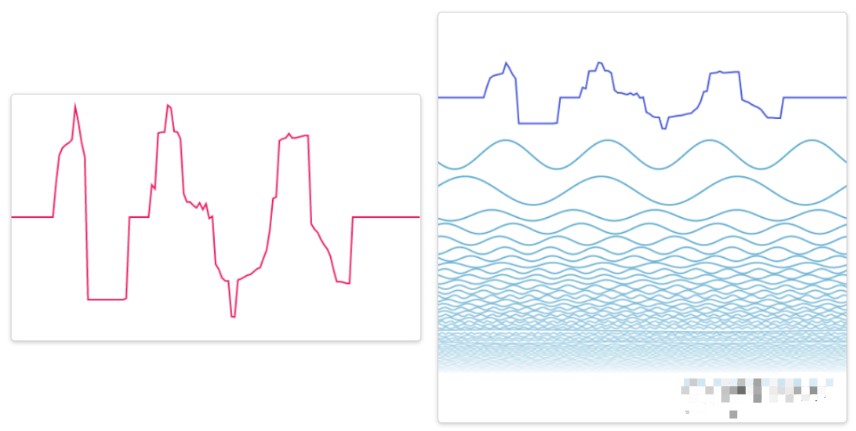
随便画一个波形都能用多个正弦波表示 和上一个方波类似，除了有些额外的摆动之外，滑块移动到中间位置，生成的波形就很接近你画的了。 我们可以利用这个事实：使用傅里叶变换，我们可以把音频中最重要的成分表达出来，并且得到和原始声音非常接近的波形。

在计算机中，波形以一系列数据点的形式来存储。

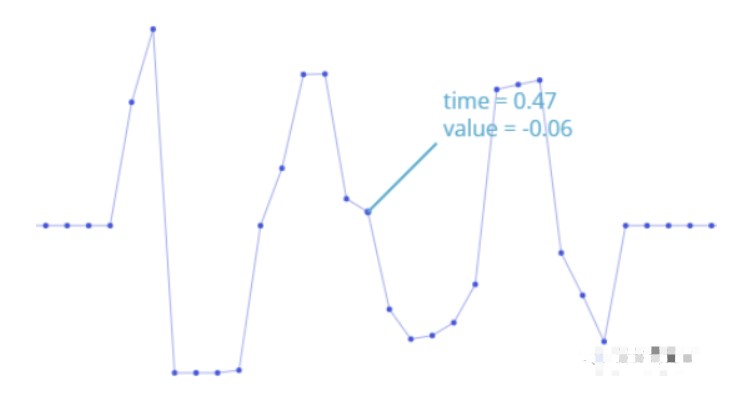
我们可以做的是，将声音表示为一堆正弦波。然后可以通过忽略掉较小幅度的高频成分来压缩声音。尽管得出的波形与原始波形不一样，但是听起来将会和原始声音很接近。

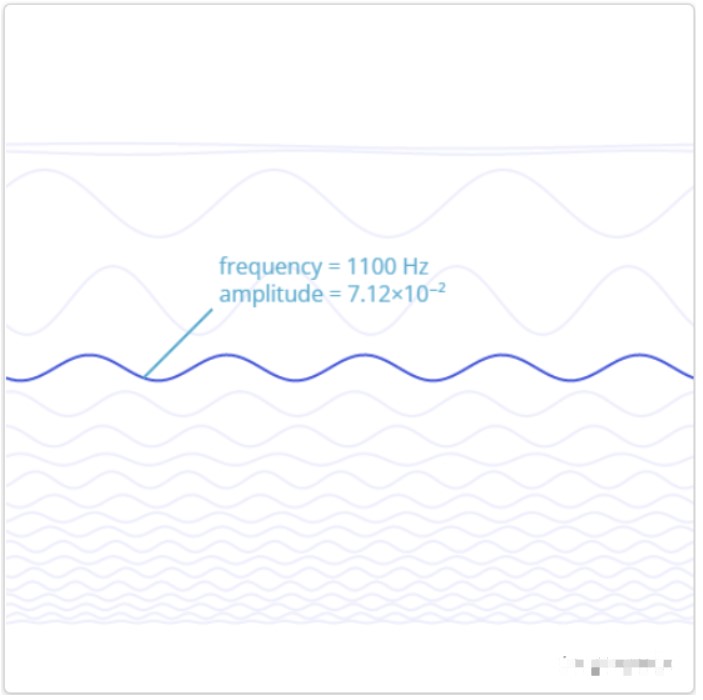
这基本上就是MP3做的事情。MP3除此之外还可以更聪明地知道需要保留哪些频率以及扔掉哪些频率。

所以在这种情况下，我们可以使用傅里叶变换来理解波的基本属性，然后我们可以将它用于数据的压缩之类的事情。

好的，现在让我们深入了解傅立叶变换。下一部分看起来很酷，也让你更加了解傅立叶变换的作用。但大多只是“看起来”很酷。

二、周转圆

在开始时，我介绍了傅里叶变换可以将事物分成正弦波。但更酷的是，它产生的正弦波不仅仅是一般的正弦波，它们都是“三维”的正弦波。你可以称之为“复杂的”正弦曲线，或者，“螺旋”。

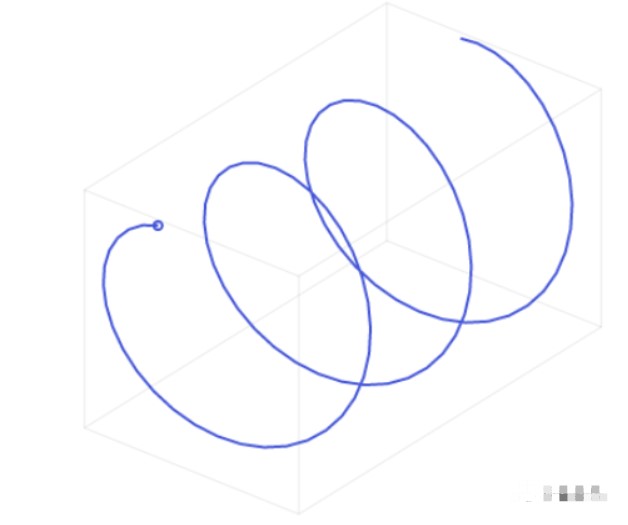
如果我们从侧面看，它们看起来像正弦波。但是，从正面看，它们看起来像圆圈。

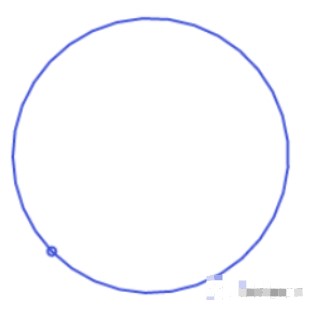
到目前为止，我们所做的一切只需要常规的2D正弦波。当我们对2D波进行傅里叶变换时，“复杂的”部分被忽略了，所以我们最终也只能得到正弦波。 但是我们可以使用3D正弦波来制作看起来很有趣的东西，就像这个：

这里发生了什么事情呢？ 我们可以将一个手绘图理解为一个3D的形状，因为点的位置在随时间移动。如果你想象一个人正在绘制一只手，那么这三个维度就代表了某一时刻铅笔尖的位置。除了x和y维度告诉我们笔尖的位置，还有一个时间维度。

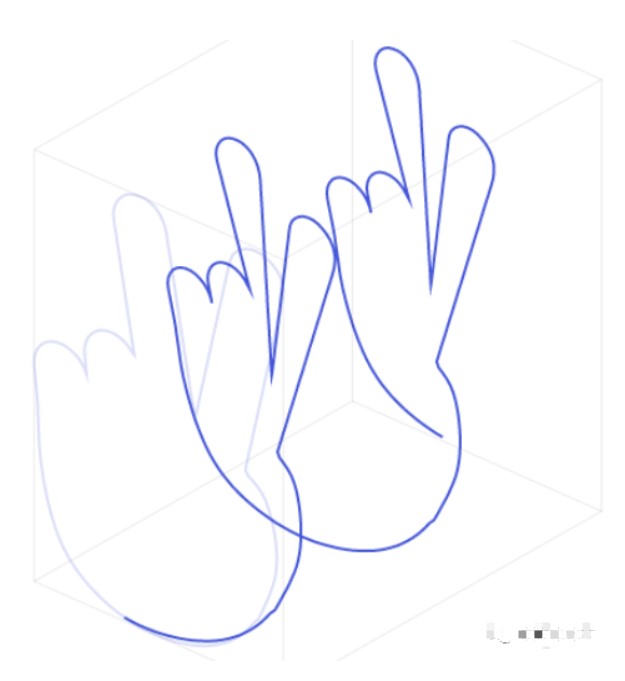
现在我们有一个3D的形状，我们不能使用常规2D正弦波把它表示出来。无论我们添加多少2D正弦波，我们都永远不会得到3D。所以我们需要些别的东西。

我们可以使用的是之前的3D螺旋正弦波。如果我们添加很多这些螺旋，得到的东西就看起来像我们的3D形状。

请记住，当我们从前面看它们时，这些波浪看起来像圆圈。围绕另一个圆圈移动的圆圈图案，被称为“周转圆”。

同样，你会发现，对于大多数形状，我们可以用很少的圆圈很好地近似表达它们，要保存一个形状，我们不必保存形状上所有的点。

这个方法可以应用于实际数据吗？答案是可以！实际上，我们有另一种称为SVG的数据格式，比我们在这里绘制图案更好用一些。所以目前，我们只是制作了些炫酷的小GIF。

然而，还有另一种类型的视觉数据使用傅里叶变换。

三、JPEG

您知道傅里叶变换也可以用于图像吗？事实上，我们一直在使用它，因为JPEG就是这样工作的！我们将相同的原理应用于图像 - 将某些东西分成一堆正弦波，然后只存储重要的正弦波。

现在我们正在处理图像，我们需要一种不同类型的正弦波。我们需要有一些东西，无论我们有什么图像，我们都可以把这些正弦波加起来，回到我们原来的图像。

要做到这一点，我们的每个正弦波也将是图像。现在，我们不再使用波浪线，而是带有黑白部分的图像。为了表示波浪的大小，每个图像将具有或多或少的对比度。

我们也可以使用它们以相同的方式表示颜色，但现在让我们从黑白图像开始。为了表示无色图像，我们需要一些水平波图像，

还有一些垂直的波图案。

就其本身而言，只有水平和垂直图像还不足以表达出我们可以看到的图像。我们还需要一些额外的图案，将两者相乘。

要得到一个8x8分辨率的图像，这里是我们需要的所有小图案。

如果我们把这些小图案的对比度调整到适当的值，然后将它们相加，我们就可以得出任意图像。

让我们从一个字母"A"开始。它非常小，但我们需要它很小，否则我们最终会得到太多其他的图像。

随着我们添加越来越多的这些图案，我们最终得到的东西越来越接近实际图像。我觉得你只要添加很少一部分图案，就能看出字母“A”的样子来。

对于实际的JPEG图像来说，这就是基本原理，剩下的只有一些额外的细节。图像被分解为8x8块，每个块分别进行分解。我们使用一组频率来确定每个像素的亮度或暗度，然后是另外两组用于颜色，一组用于红绿色，另一组用于蓝黄色。我们为每个块使用的频率个数决定了JPEG图像的品质。

这是一个实际的JPEG图像，放大后我们可以看到细节。当我们改变JPEG品质水平时，可以观察出画质的区别。

四、结论 让我们回顾一下：

傅里叶变换让我们输入一个事物，并将其分解为不同频率的成分

频率告诉我们有关数据的一些基本属性

并且可以通过仅存储重要的成分来压缩数据

我们还可以用傅里叶变换的原理，通过一堆圆圈制作看起来很酷的动画

这只是表面上的一些浅层次应用。傅里叶变换是一个非常强大的工具，因为将事物分解成不同频率是十分重要的分析方法。它们被用于许多领域，包括电路设计，移动网络信号，磁共振成像（MRI）和量子物理！

审核编辑：刘清