挺久没写动态规划相关的题目了,本文我带大家复习一下动态规划相关问题的一系列解题套路,然后着重讨论一下动态规划穷举时不同视角的问题。
动态规划解题组合拳
首先,前文我的刷题心得讲了,我们刷的算法问题的本质是「穷举」,动态规划问题也不例外,你必须想办法穷举所有可能的解,然后从中筛选出符合题目要求的解。
另外,动态规划问题穷举的过程中会出现重叠子问题导致的冗余计算,所以前文动态规划核心套路框架中告诉你如何一步一步把暴力穷举解法优化成效率更高的动态规划解法。
然而,想要写出暴力解需要依据状态转移方程,状态转移方程是动态规划的解题核心,可不是那么容易想出来的。不过,前文动态规划设计:数学归纳法告诉你,思考状态转移方程的一个基本方法是数学归纳法,即明确dp函数或数组的定义,然后使用这个定义,从已知的「状态」中推导出未知的「状态」。
还没完,比如高楼扔鸡蛋问题中对dp函数/数组的定义不见得是唯一的,不同的定义会导致状态转移方程发生变化,解题效率也有高低之分,所以我们应该给dp函数尽可能想出更合适的定义来解题。
接下来就是本文要着重探讨的问题了:就算dp函数/数组的定义相同,如果你使用不同的「视角」进行穷举,效率也不见得是相同的。
关于穷举「视角」的问题,前文回溯算法穷举视角:子集划分问题讲了回溯算法中不同的穷举视角导致的不同解法,其实这种视角的切换在动态规划类型问题中依然存在。前文对排列的举例非常有助于你理解穷举视角的问题,这里再简单提一下。
排列问题的两种视角
我们先回顾一下以前学过的排列组合知识:
1、P(n, k)(也有很多书写成A(n, k))表示从n个不同元素中拿出k个元素的排列(Permutation/Arrangement);C(n, k)表示从n个不同元素中拿出k个元素的组合(Combination)总数。
2、「排列」和「组合」的主要区别在于是否考虑顺序的差异。
3、排列和组合总数的计算公式如下:
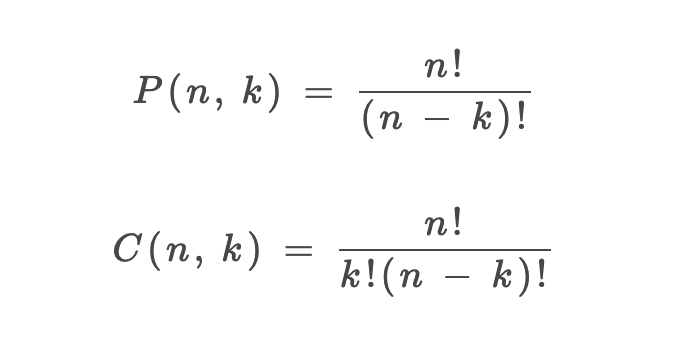
好,现在我问一个问题,这个排列公式P(n, k)是如何推导出来的?为了搞清楚这个问题,我需要讲一点组合数学的知识。
排列组合问题的各种变体都可以抽象成「球盒模型」,P(n, k)就可以抽象成下面这个场景:

即,将n个标记了不同序号的球(标号为了体现顺序的差异),放入k个标记了不同序号的盒子中(其中n >= k,每个盒子最终都装有恰好一个球),共有P(n, k)种不同的方法。
现在你来,往盒子里放球,你怎么放?其实有两种视角。
首先,你可以站在盒子的视角,每个盒子必然要选择一个球。
这样,第一个盒子可以选择n个球中的任意一个,然后你需要让剩下k - 1个盒子在n - 1个球中选择:
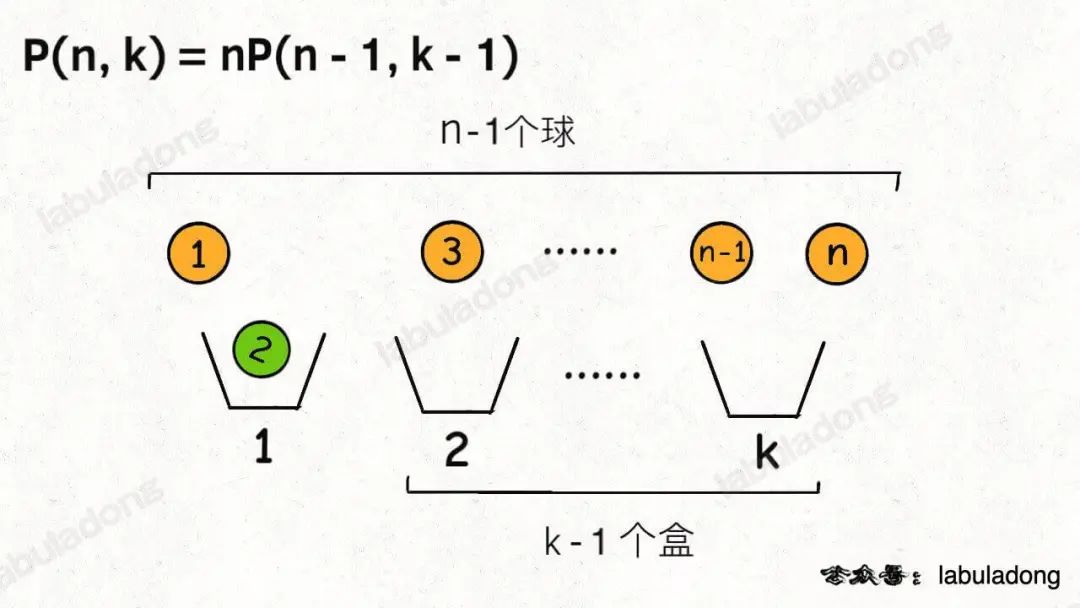
另外,你也可以站在球的视角,因为并不是每个球都会被装进盒子,所以球的视角分两种情况:
1、第一个球可以不装进任何一个盒子,这样的话你就需要将剩下n - 1个球放入k个盒子。
2、第一个球可以装进k个盒子中的任意一个,这样的话你就需要将剩下n - 1个球放入k - 1个盒子。
结合上述两种情况,可以得到:
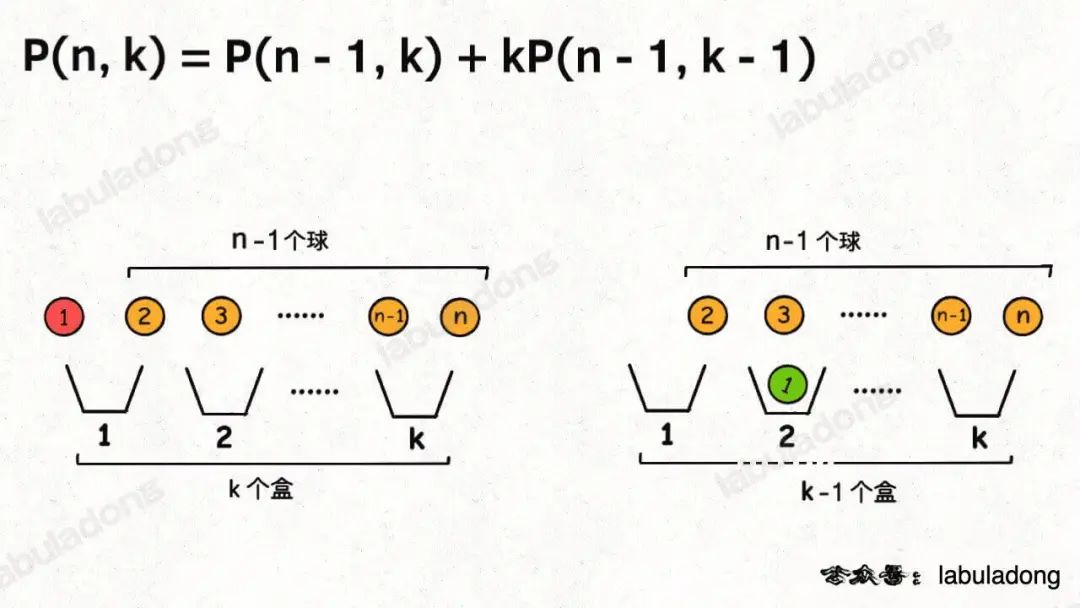
你看,两种视角得到两个不同的递归式,但这两个递归式解开的结果都是我们熟知的阶乘形式:
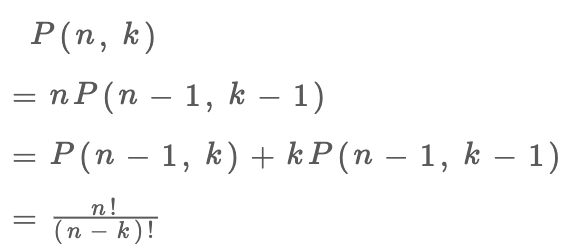
至于如何解递归式,涉及数学的内容比较多,这里就不做深入探讨了,有兴趣的读者可以自行学习组合数学相关知识。
当然,以上只是纯数学的推导,P(n, k)的计算结果也仅仅是一个数字,所以以上两种穷举视角从数学上讲没什么差异。但从编程的角度来看,如果让你计算出来所有排列结果,那么两种穷举思路的代码实现可能会产生性能上的差异,因为有的穷举思路难免会使用额外的 for 循环拖慢效率,这也是前文回溯算法穷举视角:子集划分问题主要探讨的。
本文不讲回溯算法和排列组合,不过请你记住这个例子,待会会把这种穷举视角的差异运用到动态规划题目当中。
例题分析
看一下力扣第 115 题「不同的子序列」:给你输入一个字符串s和一个字符串t,请你计算在s的子序列中t出现的次数。比如题目给的例子,输入s = "babgbag", t = "bag",算法返回 5:

函数签名如下:
intnumDistinct(Strings,Stringt);
你要数一数s的子序列中有多少个t,说白了就是穷举嘛,那么首先想到的就是能不能把原问题分解成规模更小的子问题,然后通过子问题的答案推导出原问题的答案。
首先,我们可以这样定义一个dp函数:
//定义:s[i..]的子序列中 t[j..]出现的次数为 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj)
这道题对dp函数的定义很简单直接,题目让你求出现次数,那你就定义函数返回值为出现次数就可以。
有了这个dp函数,题目想要的结果是dp(s, 0, t, 0),base case 也很容易写出来,解法框架如下:
intnumDistinct(Strings,Stringt){
returndp(s,0,t,0);
}
//定义:s[i..]的子序列中 t[j..]出现的次数为 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
//basecase1
if(j==t.length()){
//t已经全部匹配完成
return1;
}
//basecase2
if(s.length()-i< t.length() - j) {
// s[i..]比 t[j..]还短,必然没有匹配的子序列
return0;
}
//...
}
好,接下来开始思考如何利用这个dp函数将大问题分解成小问题,即如何写出状态转移方程进行穷举。
回顾一下之前讲的排列组合的「球盒模型」,这里是不是很类似?t中的若干字符就好像若干盒子,s中的若干字符就好像若干小球,你需要做的就是给所有盒子都装一个小球。
所以这里就有两种穷举思路了,分别是站在t的视角(盒子选择小球)和站在s的视角(小球选择盒子)。
视角一,站在t的角度进行穷举:
我们的原问题是求s[0..]的所有子序列中t[0..]出现的次数,那么可以先看t[0]在s中的什么位置,假设s[2], s[6]是字符t[0],那么原问题转化成了在s[2..]和s[6..]的所有子序列中计算t[1..]出现的次数。
写成比较偏数学的形式就是状态转移方程:
--定义:s[i..]的子序列中 t[j..]出现的次数为 dp(s, i, t, j)
dp(s,i,t,j)=SUM(dp(s,k+1,t,j+1)wherek>=iands[k]==t[j])
翻译成代码大致就是这个思路:
//定义:s[i..]的子序列中 t[j..]出现的次数为 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
intres=0;
//在s[i..]中寻找k,使得s[k]==t[j]
for(intk=i;k< s.length(); k++) {
if(s.charAt(k)==t.charAt(j)){
//累加结果
res+=dp(s,k+1,t,j+1);
}
}
returnres;
}
这个思路应该不难理解吧,当然还可以加上备忘录消除重叠子问题,最终解法如下:
//备忘录
int[][]memo;
intnumDistinct(Strings,Stringt){
//初始化备忘录为特殊值-1
memo=newint[s.length()][t.length()];
for(int[]row:memo){
Arrays.fill(row,-1);
}
returndp(s,0,t,0);
}
//定义:s[i..]的子序列中 t[j..]出现的次数为 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
//basecase1
if(j==t.length()){
return1;
}
//basecase2
if(s.length()-i< t.length() - j) {
return0;
}
//查备忘录防止冗余计算
if(memo[i][j]!=-1){
returnmemo[i][j];
}
intres=0;
//执行状态转移方程
//在s[i..]中寻找k,使得s[k]==t[j]
for(intk=i;k< s.length(); k++) {
if(s.charAt(k)==t.charAt(j)){
//累加结果
res+=dp(s,k+1,t,j+1);
}
}
//存入备忘录
memo[i][j]=res;
returnres;
}
这道题就解决了,不过效率不算很高,我们可以粗略估算一下这个算法的时间复杂度上界,其中M, N分别代表s, t的长度,算法的「状态」就是dp函数参数i, j的组合:
带备忘录的动态规划算法的时间复杂度
=子问题的个数x函数本身的时间复杂度
=「状态」的个数x函数本身的时间复杂度
=O(MN)*O(M)
=O(N*M^2)
当然,因为 for 循环的复杂度不总是 O(M) 且子问题个数肯定小于 O(MN),所以这是复杂度的粗略上界。不过根据前文算法时空复杂度使用指南的描述,这个上界还是说明这个算法的复杂度有些偏高。主要高在哪里呢?对「状态」的穷举已经有了memo备忘录的优化,所以 O(MN) 的复杂度是必不可少的,关键问题出在dp函数中的 for 循环。
是否可以优化掉dp函数中的 for 循环呢?可以的,这就需要另一种穷举视角来解决这个问题。
视角二,站在s的角度进行穷举:
我们的原问题是计算s[0..]的所有子序列中t[0..]出现的次数,可以先看看s[0]是否能匹配t[0],如果不匹配,那没得说,原问题就可以转化为计算s[1..]的所有子序列中t[0..]出现的次数;
但如果s[0]可以匹配t[0],那么又有两种情况,这两种情况是累加的关系:
1、让s[0]匹配t[0],那么原问题转化为在s[1..]的所有子序列中计算t[1..]出现的次数。
2、不让s[0]匹配t[0],那么原问题转化为在s[1..]的所有子序列中计算t[0..]出现的次数。
为啥明明s[0]可以匹配t[0],还不让它俩匹配呢?主要是为了给s[0]之后的元素匹配的机会,比如s = "aab", t = "ab",就有两种匹配方式:a_b和_ab。
把以上思路写成状态转移方程:
//定义:s[i..]的子序列中 t[j..]出现的次数为 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
if(s[i]==t[j]){
//匹配,两种情况,累加关系
returndp(s,i+1,t,j+1)+dp(s,i+1,t,j);
}else{
//不匹配,在s[i+1..]的子序列中计算t[j..]的出现次数
returndp(s,i+1,t,j);
}
}
依照这个思路,再加个备忘录消除重叠子问题,可以写出如下解法:
int[][]memo;
intnumDistinct(Strings,Stringt){
//初始化备忘录为特殊值-1
memo=newint[s.length()][t.length()];
for(int[]row:memo){
Arrays.fill(row,-1);
}
returndp(s,0,t,0);
}
//定义:s[i..]的子序列中 t[j..]出现的次数为 dp(s, i, t, j)
intdp(Strings,inti,Stringt,intj){
//basecase1
if(j==t.length()){
return1;
}
//basecase2
if(s.length()-i< t.length() - j) {
return0;
}
//查备忘录防止冗余计算
if(memo[i][j]!=-1){
returnmemo[i][j];
}
intres=0;
//执行状态转移方程
if(s.charAt(i)==t.charAt(j)){
//匹配,两种情况,累加关系
res+=dp(s,i+1,t,j+1)+dp(s,i+1,t,j);
}else{
//不匹配,在s[i+1..]的子序列中计算t[j..]的出现次数
res+=dp(s,i+1,t,j);
}
//结果存入备忘录
memo[i][j]=res;
returnres;
}
这个解法中dp函数递归的次数,即状态i, j的不同组合的个数为 O(MN),而dp函数本身没有 for 循环,即时间复杂度为 O(1),所以算法总的时间复杂度就是 O(MN),比刚才的解法要好一些,你提交这个解法代码,耗时明显比刚才的解法少一些。
至此,这道题就分析完了。我们分别站在t的视角和s的视角运用dp函数的定义进行穷举,得出两种完全不同但都是正确的状态转移逻辑,不过两种逻辑在代码实现上有效率的差异。
那么不妨进一步思考一下,什么样的动态规划题目可能产生「穷举视角」上的差异?换句话说,什么样的动态规划问题能够抽象成经典的「球盒模型」呢?
--- EOF ---
审核编辑 :李倩
-
函数
+关注
关注
3文章
4333浏览量
62726 -
数组
+关注
关注
1文章
417浏览量
25974
原文标题:论动态规划穷举的两种视角
文章出处:【微信号:TheAlgorithm,微信公众号:算法与数据结构】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
AMC1204有两种封装,SOIC-8和SOIC-16,功能一样吗?为什么要推出两种封装?
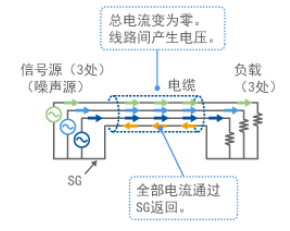
两种电缆类型的特点及优势
晶闸管的阻断状态有两种是什么
接地保护分为哪两种方式
plc与传感器的两种连接方式
wdm设备的两种传输方式
充电桩为什么有直流与交流两种接口?
800G光模块的两种主流封装
GYFTA、GYFTY两种光缆的区别
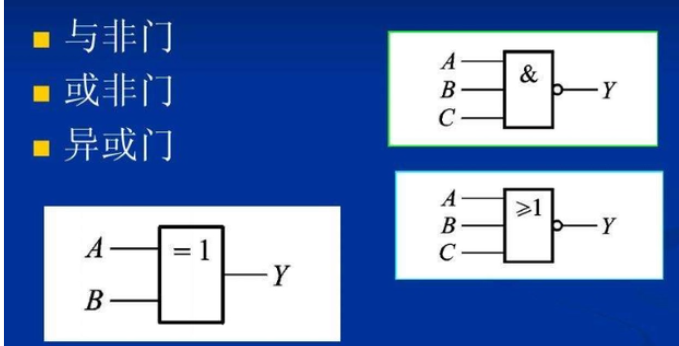
异或门两种常见的实现方式




 论动态规划穷举的两种视角
论动态规划穷举的两种视角











评论