现代 IRST(红外瞄准和跟踪)传感器可以有效跟踪敌方目标(在意大利,我们拥有出色的 Skyward-G,由 Selex Galileo 开发)。然而,达到目标的问题仍然悬而未决。在本文中,我们提出了一种自动跟踪算法,其中目标执行回避随机游走;另一方面,算法的收敛(即到达/摧毁目标)是一个确定性的过程。
一点历史
根据一个著名的轶事,在 1980 年代,斯德哥尔摩委员会没有将诺贝尔奖授予美国著名物理学家 R. Dicke,因为他将几年的职业生涯致力于实现红外传感器用于研究/跟踪/杀死移动目标。更准确地说,红外搜索和跟踪 (IRST) 传感器检测飞机废气发出的红外辐射。1950 年代使用的第一个模型相当原始,旋转自由度降低。对此类探测器后续发展的一个显着贡献来自越南战争,这也归功于迪克的开创性工作:新一代传感器看到了美国响尾蛇导弹上的光。
维纳滤波器和 IRST 传感器
IRST 传感器是飞机尾气发出的红外辐射的探测器。众所周知,任何热物体都会发射红外范围内的电磁辐射。如果这种发射类似于在温度T处处于热力学平衡状态的黑体,如果λ是发射辐射的波长,我们有位移定律:

其中λ max是发射功率最大的波长值。从这个方程可以看出,这个大小与温度成反比。在IRST传感器的实现中,需要参考一个温度范围(T 1 ,T 2),使波长落在红外波段。为了更清楚,在图 1 中,我们报告了作为无量纲变量hν / kT函数的发射功率趋势,其中h是普朗克常数,k是玻尔兹曼常数,ν = c /λ 是发射频率辐射 ( c是光速)。从温度升高时绘制的曲线族中,我们看到随着温度升高,发射峰向高频移动。
从操作上讲,IRST 传感器是一种热像仪,能够检测 2 之间波长范围的红外辐射。5 × 10 -8和 11 × 10 -8厘米。然而,主要问题是由于电磁场在红外范围内在地球大气层中传播的能力很差。更准确地说,红外光子被大气中存在的水蒸气分子吸收。因此,为了获得良好的效率,它们运行的距离不得超过指定的阈值。此外,为了对目标图像进行可能的软件重建,需要为系统配备维纳滤波器。1如果不是这样,一群鸟很可能被误认为是敌机。
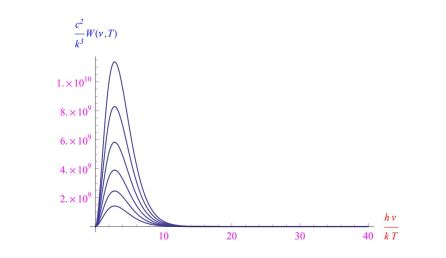
图 1:黑体在温度T的热平衡中发射的功率密度趋势(对于该量的不同值)作为无量纲变量hν / kT的函数
动态设置
地面参考系
动态设置跟踪问题意味着编写运动微分方程或应用牛顿第二定律。因此,有必要指定一个惯性参考系。由于飞机速度比表征地球运动(绕轴自转、绕太阳公转)的相应运动学量高几个数量级,因此可以非常近似地认为我们的星球是“静止的”。因此,让我们假设一个由笛卡尔坐标轴组成的 Oxyz 三元组作为参考系统 ,假设地球中心的原点为球形;x 轴在赤道平面内并朝向脚 格林威治子午线(脚是子午线与赤道平面的交点)。在这种情况下,飞机的地理坐标(纬度和经度)和高度可以很容易地转换为笛卡尔坐标(x,y,z)。
时间分辨率和飞机机动性
在这种动态场景中, 配备 IRST 传感器的攻击者(导弹)A 必须检测目标(战斗机)B。必须快速连续执行检测,以便能够将其速度矢量指向瞬时位置的目标。如果Δt 是表征上述序列的最小时间间隔,则检测到的轨迹是真实轨迹中的一段。后者显然是微分几何意义上的平滑曲线。还必须考虑单个车辆的机动性。为此,我们用 ( δt) A 和 ( δt) B表示 分别为 A 和 B 的机动时间。由于战斗机比导弹更机动,我们预计以下双重不等式:

换句话说,目标的航向变化(即规避机动)在攻击者的时间尺度上是瞬时的,并且与Δt相比都小到可以忽略不计。这种情况表明忽略上述时间尺度。这相当于假设两架飞机都具有无限机动性。最后,为了使问题在数学上更易于管理,我们执行通过 Δ t → 0 的限制的操作。这相当于直接考虑真实轨迹,将单个车辆通过一个质点进行模式化以忽略旋转自由度。这种方法可能看起来不切实际,但它构成了解决所提出问题的第一个近似步骤。
IRST 运动学
首先,我们观察到追击并不自动意味着可达性:攻击者 A 可以无限期地追击目标 B,但从未到达目标 B。在任何情况下,重要的是通过以下方式数学表达以下条件逐步进行。在图 2 中,我们报告了飞机在通用时刻 t相对于地面参考系统的位置,其中 D ( t ) 是 距离向量,其模数是上述时刻 A 点和 B 点之间的欧几里得距离。 但是让我们通过指定图中的符号来尝试更清楚。
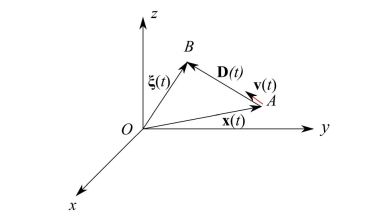
图 2:飞机相对于指定的地面三元组的瞬时位置
这里,ξ ( t ) 是目标的位置向量,即从原点向目标瞬时位置标记的向量:
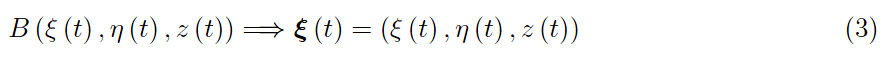
我们用希腊字母来区分它们与拉丁同音字,我们将用它来表示 A 的坐标。实际上,后者位于
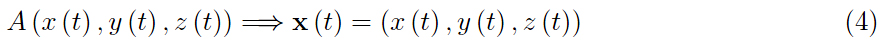
我们不知道目标的坐标,但是追击的条件是通过强加 A 的速度矢量始终指向 B 的瞬时位置来表达的(换句话说,攻击者没有预料到目标的移动) 。 从向量演算中,我们知道两个向量是平行且等价的当且仅当它们是成比例的并且比例的标量是非负的:
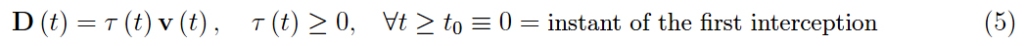
这个等式定义了“距离”向量:

其模块是:
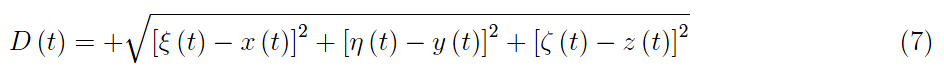
根据等式 5,我们有:

τ (t)的运动学意义 由此而来:这个量是用速度 v ( t ) 行进距离 D ( t ) 所需的时间。很明显,A 到达 B 当且仅当存在一个瞬间 t * 使得 D ( t * ) = 0 或相同的 τ ( t *) = 0。以下条件由等式 5 表示,而可达性是一个更强的条件,在某种意义上,除了前一个条件之外,在函数 τ (t) 的有限处存在零。 顺便说一句,如果正函数的唯一零在无穷远处,则相应的成就是渐近的(即,必须经过无穷大的时间)。如果

攻击者不能接近最小距离。这些考虑提出了以下定义: τ ( t ) 是碰撞时间。我们注意到这个大小不能从运动学数据中确定。相反,它必须是先验的,然后才能确定我们正在建模的战争冲突的结果。根据等式 5 并考虑到等式 6,可得出:
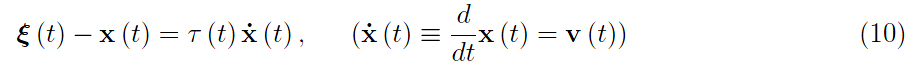
该方程可以逐个分量地写出(根据坐标轴 x、y、z),得到一阶微分方程组:

其中,连同初始条件
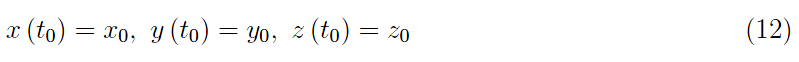
它唯一地确定了解决方案,从而确定了攻击者的轨迹。我们称 (11) 跟踪方程或追踪方程。为了在Mathematica计算环境中执行模拟, 最好在二维中工作,抑制系统 (11) 的第三个方程(我们将立即得出的结论推广到通常的三维)。所以让我们重写:
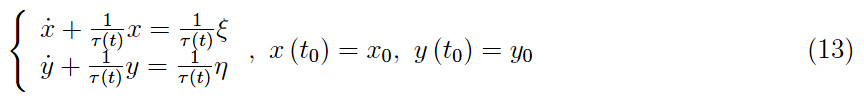
(13) 型微分方程的特点在于解具有初始瞬态 ,然后让位于稳态解。换言之,在初始阶段之后,追踪轨迹经历了稳定。例如,在图 3 中,显示了一些跟踪帧,但没有实现,因为我们使用 τ ( t ) = τ 0 》 0。由于初始条件的特定选择,在这种情况下,没有初始瞬态,并且跟踪轨迹本身就是一个圆。我们观察到存在追逐,因为攻击者的速度矢量(蓝点)朝向目标的瞬时位置(红点)。
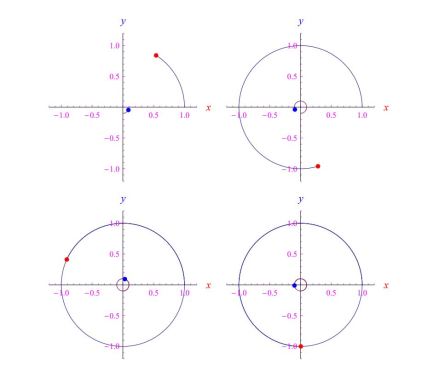
图 3:红点穿过指定的圆周,而蓝点跟随红点,因为速度矢量指向红点的瞬时位置。很明显,蓝色永远不会变成红色,因为我们设置了 τ (t) = τ0 》 0。
在图 4 中,我们报告了一些带有初始瞬态的追逐帧。如您所见,轨迹非常具有启发性。我们可以假设以下类型的线性定律,而不是考虑函数 τ ( t ) 相同地恒定(并且为正):
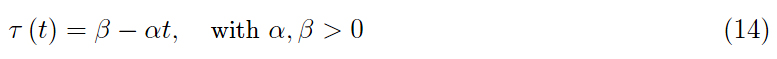
其成就时刻为 t * = β / α。 α = 10 , β = 0的前一种情况(循环 跟踪)。2,整合跟踪方程,我们得到图5的帧。在更现实的场景中,目标以随机模式执行规避机动或执行随机游走。众所周知,后者是维纳过程。2Mathematica 计算环境允许快速实施此过程。准确地说,通过一个数组的插值,它的元素是白噪声假定的值,我们得到一个在数学分析意义上实际上是时间函数的量。换句话说,进入跟踪方程 (13) 的目标坐标被视为通常的函数,因此可以通过 Mathematica 执行 它们的积分,从而知道跟踪的轨迹。在图 6 中,我们报告了随机游走中目标的一些追踪/实现帧,而在图 7 中,绘制了两架飞机的速度。目标是清晰的白噪声。
结论
追踪方程(11)作用于攻击者速度矢量的方向和方向。另一方面, 函数τ ( t ) 作用于该向量的模,即,作用于标量函数v ( t )。
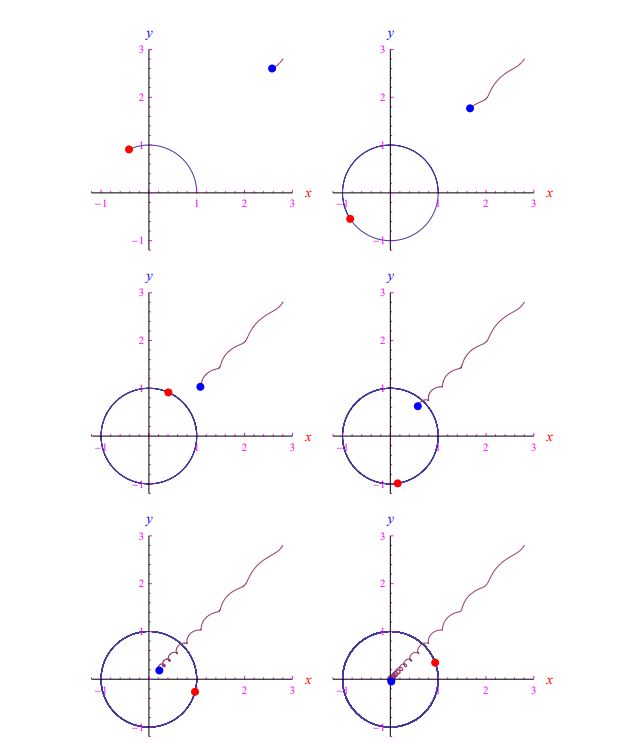
图 4:术语“瞬态”描述了一条曲线,直到它停留在半径 1/√401 的圆周上。
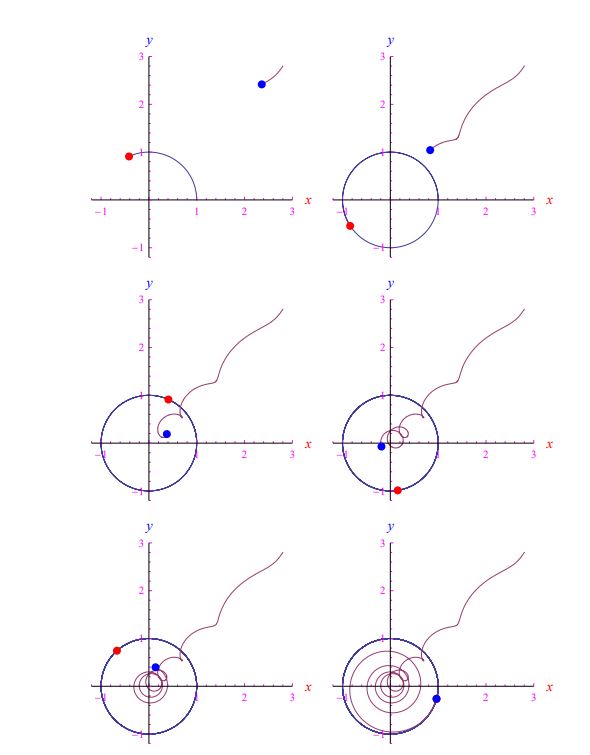
图 5:攻击者在时间t * = 50(无量纲单位)后到达目标。
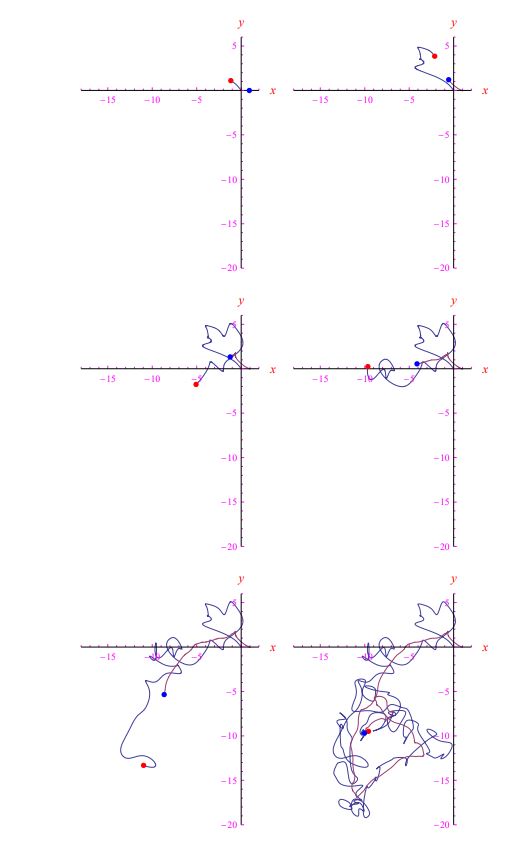
图 6:攻击者在时间t * = 200(无量纲单位)后到达目标。
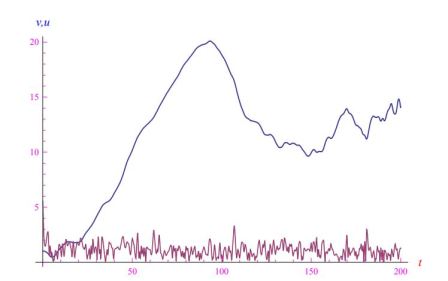
图 7:速度与时间(无量纲单位)
由此可见,追击是由攻击者通过 ξ (t) 决定的,而碰撞是由 τ (t) 决定的。我们的算法是一个有趣的计算实验,可以更好地理解 IRST 运动学。
审核编辑:郭婷
-
传感器
+关注
关注
2554文章
51700浏览量
758543 -
滤波器
+关注
关注
161文章
7919浏览量
179506
发布评论请先 登录
相关推荐
步进电机基础(8.2)-步进电机的问题解决方案-降低振动噪音的解决方法 相关资料分享
IPTV系统中的FPGA供电问题解决方案
altium_designer_Summer09出现的问题解决方案
手机快充的噪声问题解决方案资料下载

N76E003的EEPROM问题解决方案:使用Data Flash模拟EEPROM

C2000 F28004x系列MCU PLL锁相失败问题解决方案





 自动跟踪算法的追踪问题解决方案
自动跟踪算法的追踪问题解决方案










评论