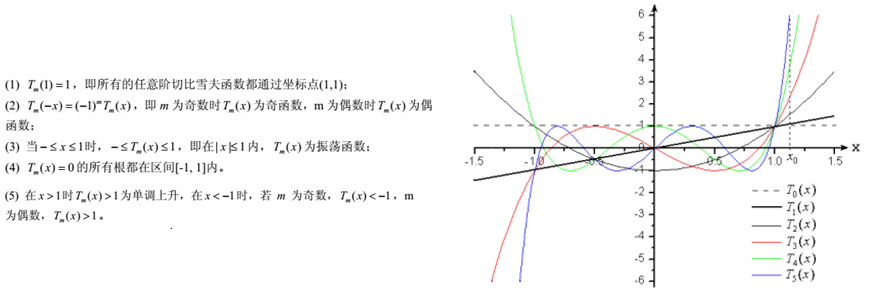
(1)等副瓣电平;
(2)在相同副瓣电平和相同阵列长度下主瓣最窄,为最佳阵列;
(3)单元数过多时,阵列两端单元激励幅度跳变大,使馈电困难。一般在雷达系统中,为了使其具有较高的抗干扰、抗反辐射导弹的能力,往往要求雷达天线的副瓣尽量低,而采用道尔夫-切比雪夫综合法以及进一步的泰勒综合法等设计的阵列天线就可以实现低副瓣。最早,道尔夫(C.L.Dolph)利用切比雪夫函数来逼近天线阵列的阵因子函数,得到了这种严谨规范的综合方法。而且,经过前人研究,当天线单元N≤13时,切比雪夫阵列从中间到两端的激励分布是单调减小的;而当N>13时,阵列两端单元的激励开始出现跳变。所以对于大型阵列来说一般不宜采用切比雪夫方法综合阵列。所以下面的Matlab程序正常工作在天线单元数N为3到13这个范围内。关于如何采用切比雪夫多项式去设计阵因子的具体技术步骤,另一篇文章较为详细地介绍了,此处不再赘述,大家可以在文尾或评论区查看。下面是可以综合设计天线单元从3到13单元的切比雪夫综合法的Matlab程序:|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 |
|
----END 上文提到的另一篇文章。
阵列天线综合之切比雪夫低副瓣阵列设计 MATLAB(作者:OLIVERMAHOUT)
相控阵天线中,直线阵列作为重要的一种,有着极为广泛的应用。切比雪夫低副瓣阵列设计是一种典型的设计方法。
切比雪夫方法主要是实现低副瓣、窄波束:
其产生的核心如下:
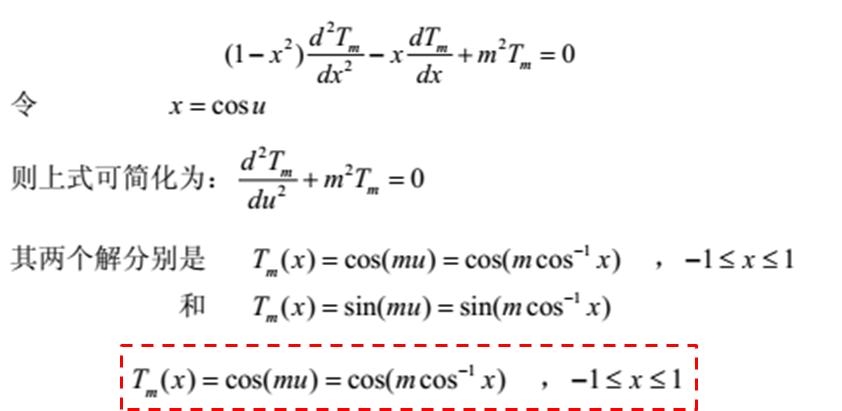
我的理解:因为能量守恒,所有副瓣都一样的时候,能量会更多的集中在副瓣中,
主瓣最大增益也不会改变,这样就可以使主瓣窄,副瓣电平降低。G=4πS/λ2
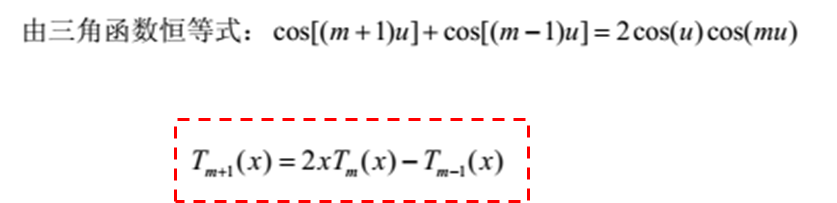
结合切比雪夫函数,可以得到:
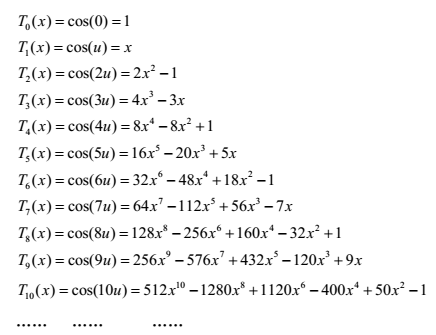

当具体应用时,解决方案如下:

话不多说,其Matlab中的程序如下:

1
% 2019-11
% 切比雪夫低副瓣阵列馈电设计_1.0 (端射阵)
close all;
clear
% digits(3);
% 参数设置
lamda = 1; % 波长
d = lamda * 0.6; % d为阵元间距
theta0 = (120/180)*pi; % 扫描角度
theta = 0: 0.01 : pi; % Θ为方向角
u = pi*d*(cos(theta)-cos(theta0))/lamda;
%T = Chebyshev; % T为切比雪夫恒等式系数矩阵
N = 10; % N为直线阵的阵元数量,M为一侧的单元数(对称)
R0dB = 26; % R0dB为副瓣电平
if (mod(N,2)==0)
M = N / 2;
parity = 0; % parity为奇偶性,0为偶数
else
M = (N+1)/2;
parity = 1;
end
% 导入切比雪夫多项式
syms x;
T = [
1;
x;
2*x^2-1;
4*x^3-3*x;
8*x^4-8*x^2+1;
16*x^5-20*x^3+5*x;
32*x^6-48*x^4+18*x^2-1;
64*x^7-112*x^5+56*x^3-7*x;
128*x^8-256*x^6+160*x^4-32*x^2+1;
256*x^9-576*x^7+432*x^5-120*x^3+9*x;
512*x^10-1280*x^8+1120*x^6-400*x^4+50*x^2-1
];
% 换算副瓣电平R0
R0 = 10 ^ (R0dB / 20);
% 计算x0
x0 = ((R0 + sqrt(R0^2 -1))^(1/(N-1)) + (R0 - sqrt(R0^2 -1))^(1/(N-1))) * 1/2;
% 定义馈电幅度矩阵I
I = sym('I', [1 M]);
% 计算展开的方向图表达式
S = T(2) * I(1);
for k = 2 : M
S = S + T(2*k) * I(k);
end
%collect(S,x)
%vpa(S)
S_po = coeffs(S,x); % 含电流的方向图多项式系数
T_po = sym2poly(T(N)); % 标准的方向图多项式系数(反向了)
T_PO = zeros(1,M);
for k = 1 : M
T_PO(k) = T_po(2*k-1);
S_po(k) = S_po(k)/x0^(2*k-1);
end
% T_PO
% vpa(S_po)
% 系数比较求出电流大小
eq = sym('eq',[M 1]); % 系数比较恒等式
for k = 1 : M
eq(k) = S_po(k) == T_PO(M+1-k);
end
vpa(eq)
I_st = solve(eq);
I_ce = struct2cell(I_st);
i = zeros(M,1); % 最终的电流矩阵
for k = 1 : M
i(k) = I_ce{k,1};
i(k) = i(k);
end
for k = 2 : M
i(k) = i(k)/i(1); % 电流归一化
end
i(1) = 1; i
i=[1;0.89;0.706;0.485;0.357]; % 用来检验的数据
% 计算最终的阵因子
S_all = zeros(1,length(theta));
for k = 1 : M
S_all = S_all + i(k)*cos((2*k-1)*u);
end
SS = S_all;
% 画图 —— 直角坐标系
S_max = max(S_all); % 归一化处理
S_all = 20*log10(abs(S_all/S_max)); % 取分贝值
figure('NumberTitle', 'off', 'Name', 'S Parameter (dB) - Cartesian');
theta_ = theta * 180 / pi;
plot(theta_,S_all,'k','LineWidth',1.5);
grid off
xlabel(' heta (°)','FontSize',13);
ylabel('|S| dB','FontSize',12);
axis([0 182 -50 2]);
box on
% 画图 —— 极坐标系
figure('NumberTitle', 'off', 'Name', 'S Parameter (dB) - Polar');
S_pol = SS / max(SS);
polarplot(theta,S_all,'k','LineWidth',1.5);
thetalim([0 180]);
rmin = min(S_all);
rmax = max(S_all);
rlim([-50 rmax]);

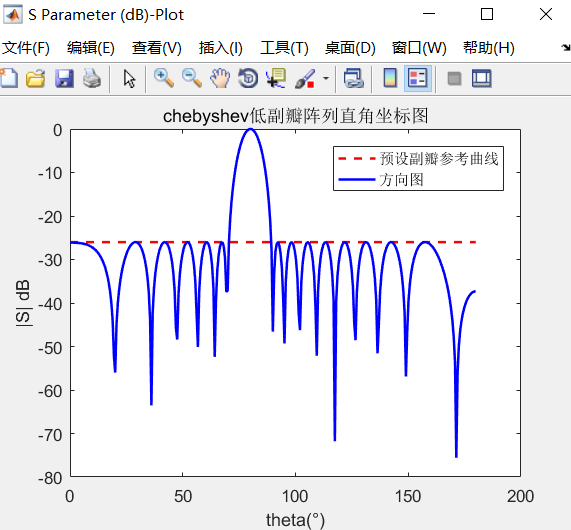
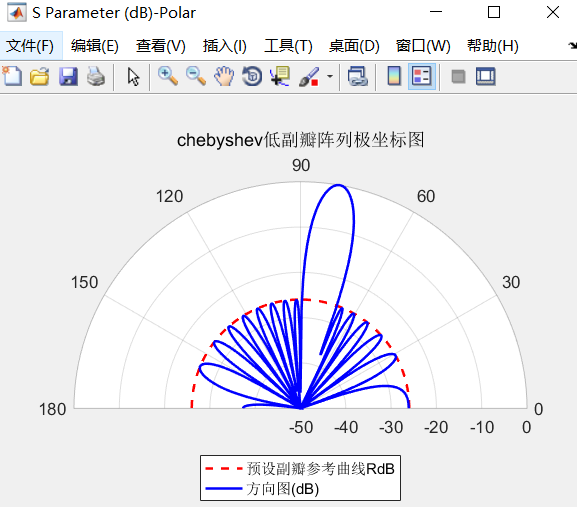
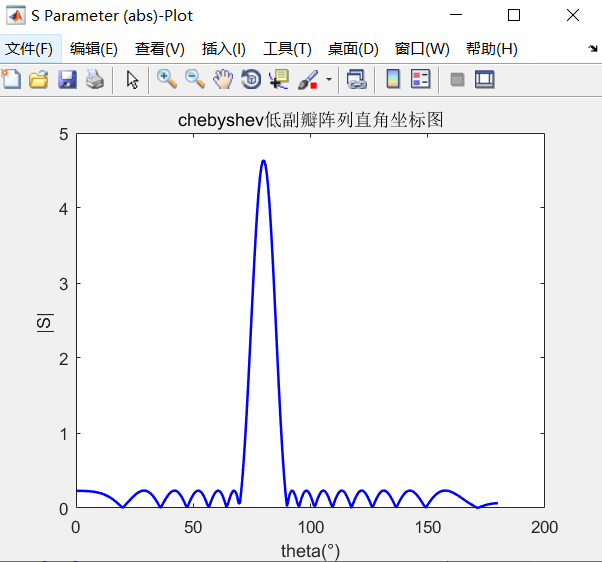
上述测试的N=10的10个阵列,侧射阵(θ=0),副瓣电平SLL=26dB,结果如下:
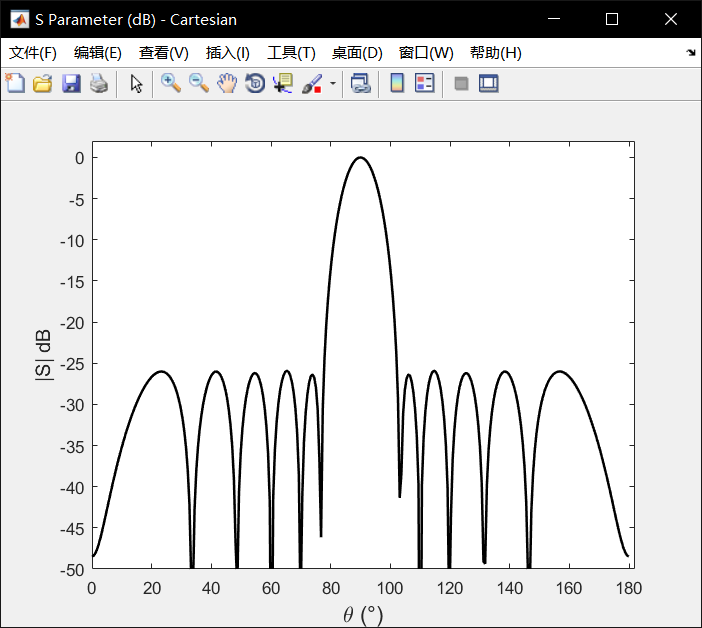
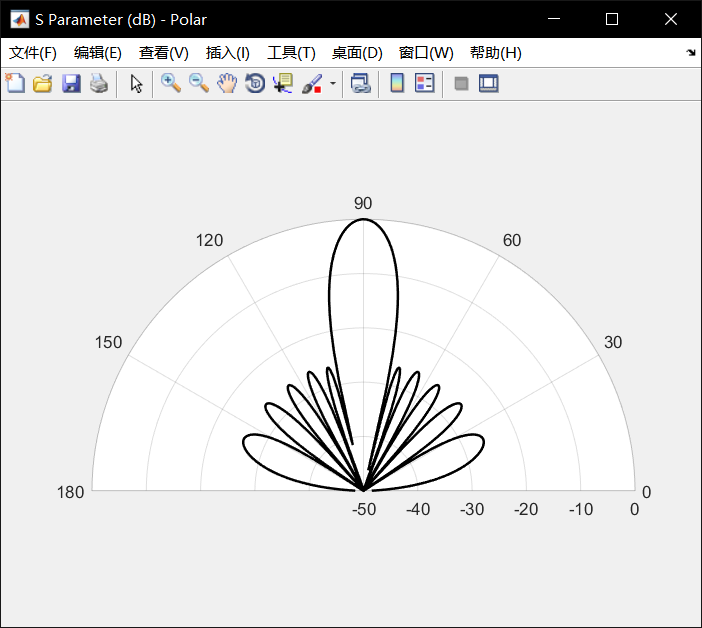
经过比较,结果较为标准。
更改一下theta0的值,改为120读,即偏离法相30度:
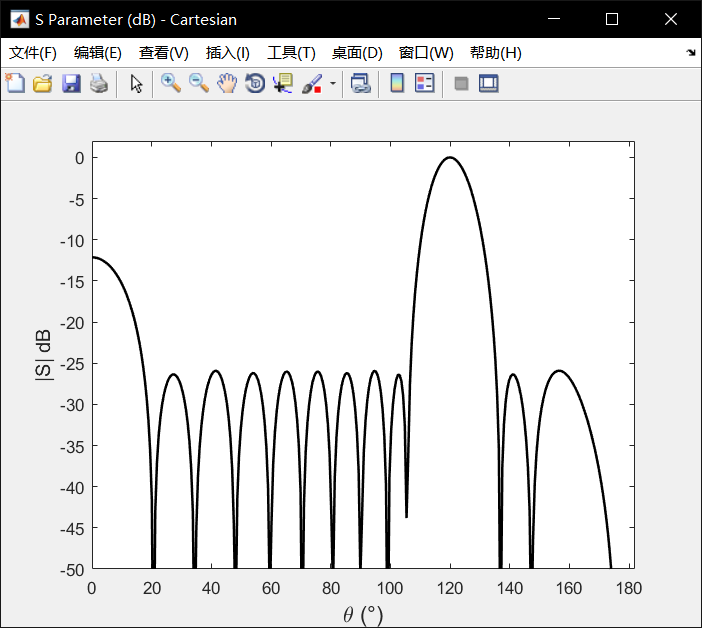
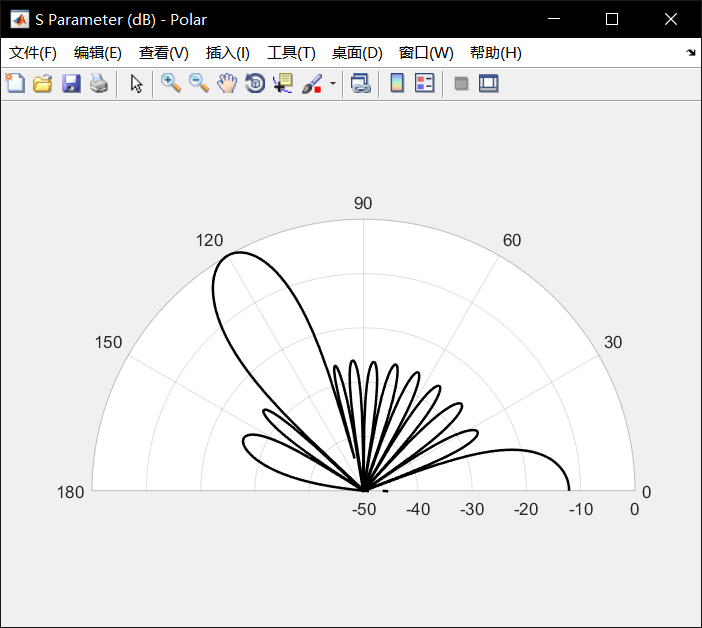
-
matlab
+关注
关注
185文章
2977浏览量
230576 -
电平
+关注
关注
5文章
360浏览量
39919 -
阵列天线
+关注
关注
3文章
33浏览量
11011
原文标题:MATLAB阵列天线之切比雪夫低副瓣阵列设计
文章出处:【微信号:ZGDZGCS,微信公众号:电子万花筒】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
VirtualLab Fusion应用:用于光束切趾的圆锯齿光阑
奥托立夫广州新工厂正式开业
使用FilterPro软件设计的带通滤波器和设定的差很多是为什么?
如何使用MATLAB创建预测模型
MATLAB如何使用训练好的网络
电力电容器手动投切和自动投切区别在哪





 切比雪夫综合法的Matlab程序
切比雪夫综合法的Matlab程序










评论