1 连续周期信号的傅里叶分解
信号的正交分解 -- 在区间上的任意能量有限信号f(t)可以用正交函数集合 中的函数的线性组合来近似表示:
式中:表示正交函数集中的函数,系数可以利用最小均方误差准则求解:
常用的完备正交函数集:
三角函数集{}
复指数函数集{}
信号在这两个函数集中分解得到的级数叫做傅里叶级数,周期信号进行傅里叶分解应该满足狄利克雷条件:
在一个周期内满足绝对可积
在一个周期内有有限个极大值和极小值
在一个周期内有有限个第一类间断点
三角傅里叶级数设f(t)为一周期为T的周期信号,且满足狄氏条件,则f(t)在区间可分解为:
式中:
T为信号周期,为基波频率(看作整体一项)。
写作余弦形式:
式中:
为偶函数,为奇函数。
指数傅里叶级数设f(t)为一周期为T的周期信号,且满足狄氏条件,则f(t)在区间可分解为:
式中:
指数傅里叶级数中负频率的出现是数学处理的结果。
复振幅表示式中,表示n次谐波分量的复振幅。
2 连续非周期信号的傅里叶变换周期信号的频谱具有离散性,非周期信号的频谱变为连续谱。
非周期信号傅里叶变换存在的充分条件是信号满足绝对可积,即:
正变换:
反变换:
与周期信号相比,中自变量连续取值,而离散取值,且满足:
若信号不满足绝对可积条件,其傅里叶变换就不存在,此时拉普拉斯变换适用,略。
3 周期序列的离散傅里叶级数(DFS)时域的周期造成频域的离散,时域的离散造成频域的周期延拓,因此周期序列的DFS也是离散的周期序列。
周期序列:
式中,r为任意整数,N为周期。DFS正变换:
DFS反变换:
式中,从DFS计算中可以看出,周期序列的DFS也是周期为N的离散序列,周期序列的DFS也具有无限个频率,仅有N个不同幅值。
4 离散傅里叶变换(DFT)长度为N的序列x(n)可以看作:
式中,表示长度为N的单位矩形序列。叫做的主值序列。DFT正变换:
DFT反变换:
从DFT的计算中可以看出,DFT的结果对应DFS一个周期的序列值。
-
频谱
+关注
关注
7文章
888浏览量
45933 -
函数
+关注
关注
3文章
4352浏览量
63250 -
傅里叶
+关注
关注
0文章
60浏览量
20600
原文标题:信号的分解
文章出处:【微信号:zhuyandz,微信公众号:FPGA之家】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
VirtualLab Fusion案例:单分子显微镜高NA成像系统的建模
VirtualLab Fusion案例:高NA傅里叶单分子成像显微镜
低压配电中产生的谐波应该如何治理?
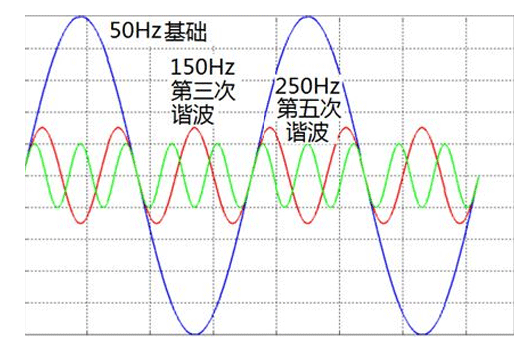
傅里叶变换的数学原理
无叶风扇灯的优缺点有哪些
傅里叶半导体荣获季丰电子AEC-Q100与AEC-Q006证书
FIR连续采样分段卷积时域重叠相加法




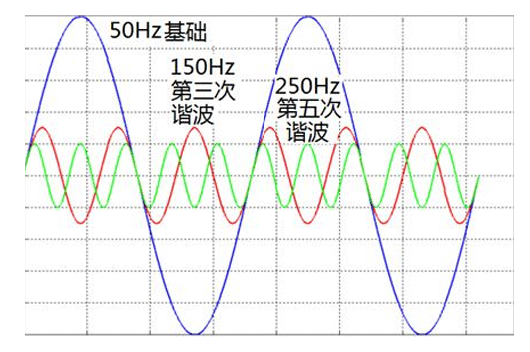
 连续周期信号的傅里叶分解
连续周期信号的傅里叶分解










评论