什么是离散时间晶体 光力系统中构造离散时间晶体

文章来源：中国科学院理论物理研究所

原文作者：陈冬妮

1、从时间到空间

晶体在我们的日常生活中随处可见，烹饪菜肴的食用盐，晶莹剔透的冰糖，水凝固后形成的冰，这些都是晶体。在微观层面上，它们是由原子按一定规则有序排列的结构。事实上，晶体的存在是原子空间连续平移对称性自发破缺的一种表现，这里的自发对称性破缺指的是系统的基态比物理系统本身的对称性低，系统的基态在哈密顿量的对称性下不能保持不变。也就是说，原子的空间连续平移对称性破缺，自组织的形成具有较低的空间离散平移对称性的周期晶体结构。

由于物理定律在时间上也是连续平移对称的，所以类比于三维空间中晶体的概念，麻省理工学院理论物理学家弗兰克•威尔切克（Frank Wilczek）于2012年首次提出了时间晶体的概念：不同于空间晶体是在三维空间中形成重复的结构，时间晶体指的是系统的最低能状态是系统处于重复运动的状态，也就是说在时间上形成稳定的周期振荡结构。自2012年时间晶体概念被提出起，是否可能在时间上打破对称性，从而创造出“时间晶体” 成了理论和实验物理学家们积极探索的问题。

2、离散时间晶体

2012年维尔切克提出了量子时间晶体模型[1]，随后，2013年加州大学的张翔团队提出以离子阱为平台实现量子时间晶体理论[2]。但是很快特里克•布鲁诺 （Patrick Bruno）和渡边悠树（Haruki Watanabe）就针对他们的工作发表了几篇文章[3,4]，证明了在有限温的平衡态情况下，只具有短程相互作用的多体物理系统，在热力学极限下不存在量子时间晶体。因此在接下来的研究中，人们逐渐将关注点转移到了在周期性调制的非平衡系统中。

2015 年克里斯托弗•萨查（Krzysztof Sacha） 发现在周期性驱动（Floquet）的冷原子系统中，系统的响应周期可以是外加驱动的周期的两倍。他认为这正好体现出了离散时间平移对称性的破缺[5]。随后，离散时间晶体的理论得到快速发展。一个哈密顿量的周期驱动（Floquet）系统，当满足以下三个条件时可以被称为处于离散时间晶体阶段[6,7]：1. 离散时间平移对称性破缺：存在观测量的周期不同于系统的驱动周期，也就是说，从变成，这里。2. 鲁棒性：晶体必须坚固耐用，这意味着系统在特定范围内存在外部波动时，当前状态的离散时间晶体行为总能维持。3. 长时性：在热力学极限满足的情况下，这种周期为的倍周期性振荡可以在无限长的时间内持续。

2016年，基于这个新概念进行了两个非常重要的实验。首先，马里兰大学的克里斯托弗·门罗（Christopher Monroe）团队在射频电磁场中捕获了一连串的镱-171离子，利用周期性激光驱动来操纵和观察它们的自旋状态。这导致它们以驱动周期的整数倍振荡，是实现离散时间晶体的确定标志。并且这种亚谐波响应行为在受到外部微扰的情况下仍然成立[8]。同年，在哈佛大学，由米哈伊尔·卢金（Mikhail Lukin）教授领导的一个研究小组使用金刚石色心系统也取得了类似的结果[9]。最近，用量子计算机模拟多体离散时间晶体也得以实现[10,11,12]。其中，谷歌团队利用谷歌的悬铃木量子处理器在链状的20个超导比特中观察到稳定的时间晶体[20]。与此同时，关于离散时间晶体的扩展理论也在蓬勃发展中，比如，基于Dicke 模型实现离散时间晶体[13]，基于里德堡原子链实现离散时间晶体[14]，拓扑离散时间晶体等[15]。

3、在光力系统中构造离散时间晶体

然后我们考虑在光腔中嵌入两个机械振子的腔光力学模型中实现离散时间晶体的方案。腔光力学主要探究的是电磁场和机械模式之间的相互作用，作为现代物理学中一个快速发展的领域，在过去的十几年中，它已成为探索宏观量子力学行为和量子信息处理最有前途的平台之一。在光腔中嵌入两个机械振子的光力学模型可以被映射到Dicke模型，在热力学极限下可以通过调节耦合参数来实现超辐射量子相变。我们可以通过以为周期来调节失谐和驱动振幅来改变相变的临界点，使得系统在超辐射量子相变的两个稳态之间切换进而实现周期为的Dicke型离散时间晶体。

基于以上原理，我们先介绍在光腔中嵌入两个机械振子的光力学模型，两个机械振子分别被放置于光学模的波峰和波谷处，因此只需要考虑相反的二阶光力学相互作用。在考虑光力学哈密顿量的线性化近似（将光场的振幅分成一个相干（经典）部分加上一个波动: ）和旋波近似下，系统的有效哈密顿量可以写为，这里()是光学模式（两个机械振子模式）的湮灭算符，是通过横梁耦合的两个机械振子之间直接相互作用强度。表示单模光腔的经典振幅，表示光腔的失谐。对于这个有效哈密顿量，总声子数是守恒量。利用Schwinger变换 有效哈密顿量可以被完全映射到Dicke模型并且具有在变换下保持不变的对称性。类比Dicke模型，这个对称性的自发破缺导致了量子相变。也就是说，在热力学极限声子数下当光力学耦合强度大于临界耦合强度时，对称性自发破缺，系统的基态发生从正常态到超辐射态的二阶量子相变，序参量从零变成具有一定的宏观占据，系统的自由能从抛物线型变成双阱势。为了方便后面的表述，我们把系统的两个超辐射稳态可以记成。

我们选取其中一个稳态作为初态（可以通过某一初态经过足够长时间演化而得到）。我们固定耦合强度，同时调整失谐和驱动幅度来调节临界耦合强度实现正常相和超辐射相的转换，进而使得系统在两个稳态之间不断切换。一个精确的倍周期Floquet动力学方案可以通过如下四个步骤得到（如图2）。其中阶段1和3，系统处于正常相，由于初值的限制，序参量将在附近振荡，我们可以选取合适的时间使其翻转。阶段2和4，系统处于超辐射相，系统逐渐演化到相应的稳态上去。如示意图(2. b)中蓝色线所示，当我们不断重复这样的行为时就可以在实现倍周期的离散时间晶体行为。在热力学极限下，示意图中黑色线表示的频闪动力学也会无止尽的振荡下去。并且通过数值模拟，我们发现在热力学极限下这种方案下的离散时间晶体行为是满足长时性以及对参数起伏有一定的鲁棒性。

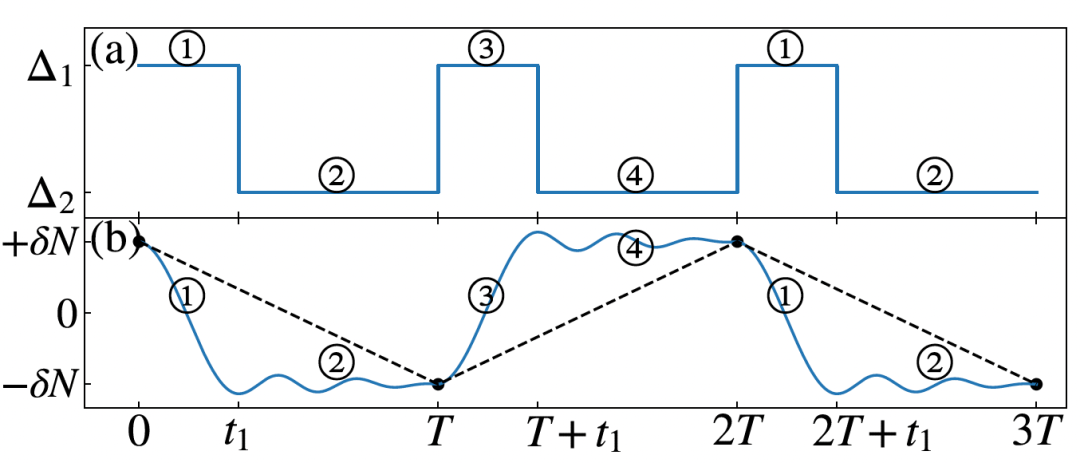
实现离散时间晶体方案示意图。

综上，我们简单介绍了时间晶体的提出，离散时间晶体的概念、时间晶体的发展以及在光腔中插入两个机械振子的光力系统模型中理论上如何产生离散时间晶体行为的方案，希望可以让读者对离散时间晶体有初步的了解。

参考文献

[1] Wilczek, Frank. "Quantum time crystals." Physical review letters 109.16 (2012): 160401.

[2] Li, Tongcang, et al. "Space-time crystals of trapped ions." Physical review letters 109.16(2012): 163001.

[3] P. Bruno, Phys. Rev. Lett. 111, 070402 (2013).

[4] H. Watanabe and M. Oshikawa, Phys. Rev. Lett. 114, 251603 (2015).

[5] K. Sacha, Phys. Rev. A, 91: 033617 (2015).

[6] A. Russomanno, F. Iemini, M. Dalmonte, and R. Fazio, Phys. Rev. B 95, 214307 (2017).

[7] B. Huang, Y. H. Wu, and W. V. Liu, Phys. Rev. Lett. 120, 110603 (2018).

[8] J. Zhang, et al, Nature, 543(7644): 217-220 (2017)

[9] S. Choi, et al, Nature, 543(7644): 221-225 (2017).

[10] X. Mi, et al. Nature , 601(7894): 531-536 (2022).

[11] H. Xu, et al, arXiv, 2021. https://arxiv.org/abs/2108.00942.

[12] X. Zhang, et al. arXiv, 2021. https://arxiv.org/abs/2109.05577.

[13] Z. Gong, et al. Phys. Rev. Lett., 120: 040404 (2018).

[14] C. H. Fan, et al. Phys. Rev. A, 2020, 101: 013417(2020).

[15] K. Giergiel, et al. New Journal of Physics, 21(5): 052003 (2019).

[16] 郭启淏、尹璋琦-时间晶体: 构想、争议与实现.

[17] https://en.wikipedia.org/wiki/Time_crystal.

编辑：黄飞