大家好,我是吴师兄,
今天的题目来源于 LeetCode 第 560 号问题:和为 K 的子数组,难度为「中等」。
一、题目描述
给你一个整数数组nums和一个整数k,请你统计并返回该数组中和为k的子数组的个数。
示例 1:
输入:nums =[1,1,1], k = 2
输出:2
示例 2:
输入:nums =[1,2,3], k = 3
输出:2
提示:
-
1 <= nums.length <= 2 * 10^4 -
-1000 <= nums[i] <= 1000 -
-10^7 <= k <= 10^7
二、题目解析
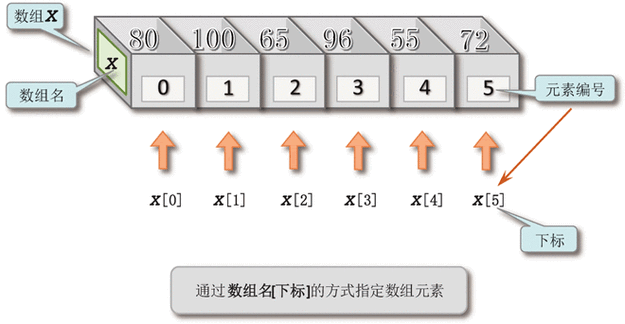
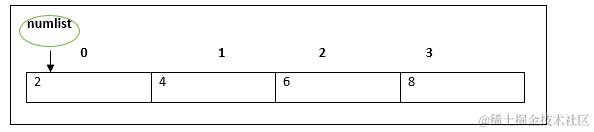
补充知识点前缀和:前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身)。
利用前缀和这种特点,可以快速的计算某个区间内的和,比如前 i 个元素的前缀和为preSum[i] = num[0] + nums[1] + ... + nums[i],而前 j 个元素的前缀和为preSum[j] = num[0] + nums[1] + ... + nums[j]。
那么区间[ i , j ]之间的子数组之和就是 **preSum[j] - preSum[i]**。
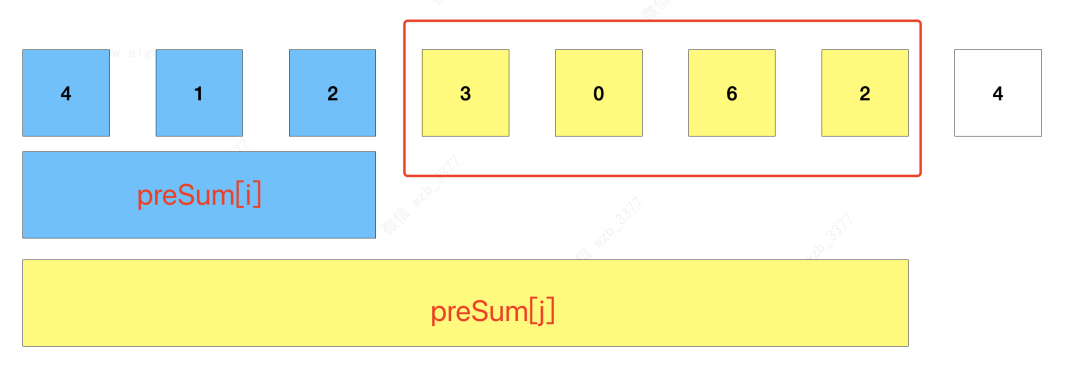
基于这种思路,可以先遍历一次数组,求出前缀和数组。
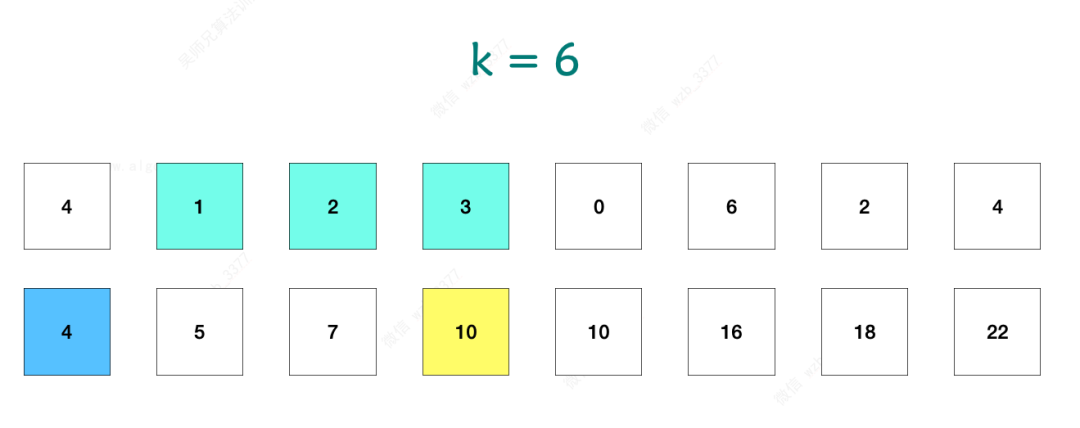
题目这个时候就变成了需要寻找出多少个 i 和 j 的组合,使得 [ i , j ] 这个区间的和为 k。
classSolution{
publicintsubarraySum(int[]nums,intk){
intlen=nums.length;
int[]preSum=newint[len+1];
preSum[0]=0;
for(inti=0;i< len; i++) {
preSum[i + 1]=preSum[i]+nums[i];
}
intcount=0;
for(inti=0;i< len; i++) {
for(intj=i;j< len; j++) {
if(preSum[j+1]-preSum[i]==k){
count++;
}
}
}
returncount;
}
}
在计算过程中,有两个 for 循环发生了嵌套,时间复杂度来到了 O(n^2) 级别。
需要优化。
事实上,我们不需要去计算出具体是哪两项的前缀和之差等于k,只需要知道等于 k 的前缀和之差出现的次数 count,所以我们可以在遍历数组过程中,先去计算以 nums[i] 结尾的前缀和 pre,然后再去判断之前有没有存储 pre - k 这种前缀和,如果有,那么 pre - k 到 pre 这中间的元素和就是 k 了。
具体操作如下:
1、利用哈希表,以前缀和为键,出现次数为对应的值,记录 pre[i] 出现的次数。
2、开始从头到尾遍历 nums 数组,在遍历过程中,会执行两个操作。
3、存储索引为 i 的这个元素时,前缀和的值是多少,并且把这个值出现的频次存储到 mp 中。
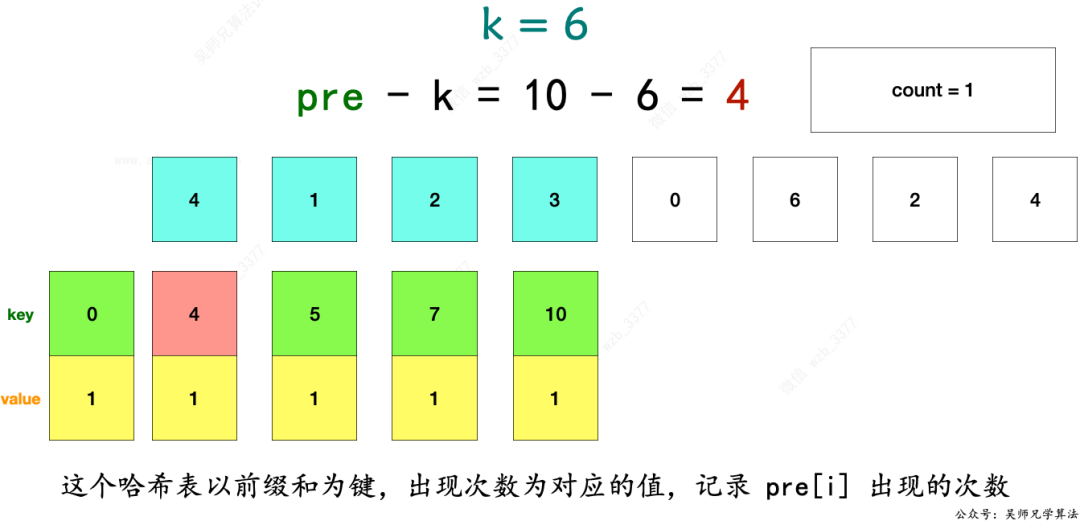
4、判断之前有没有存储 pre - k 这种前缀和,如果有,说明 pre - k 到 pre 直接的那些元素值之和就是 k。
5、返回结果。
三、参考代码
1、Java 代码
//登录AlgoMooc官网获取更多算法图解
//https://www.algomooc.com
//作者:程序员吴师兄
//代码有看不懂的地方一定要私聊咨询吴师兄呀
//和为 K 的子数组(LeetCode 560):https://leetcode.cn/problems/subarray-sum-equals-k/
classSolution{
publicintsubarraySum(int[]nums,intk){
//统计和为K的子数组的数量
intcount=0;
//记录遍历到索引为i的这个元素时,前缀和的值是多少
intpre=0;
//利用哈希表,以前缀和为键,出现次数为对应的值,记录pre[i]出现的次数
HashMapmp=newHashMap<>();
//一开始,需要设置前缀和为0时,出现的次数为1次
//这一行的作用就是为了应对nums[0]+nums[1]+...+nums[i]==k这种情况
//如数组[1,2,3,6]
//这个数组的累加和数组为[1,3,【6】,12]
//如果k=6,假如mp中没有预先存储(0,1)
//那么来到累加和为6的位置时,这时mp中存储的就只有两个数据(1,1),(3,1)
//想去判断mp.containsKey(pre-k),这时pre-k=6-6=0
//但map中没有(0,1),
//因为这个时候忽略了从下标0累加到下标i等于k的情况
//仅仅是统计了从下标大于0到某个位置等于k的所有答案
mp.put(0,1);
//开始从头到尾遍历nums数组,在遍历过程中,会执行两个操作
//1、存储索引为i的这个元素时,前缀和的值是多少,并且把这个值出现的频次存储到mp中
//2、判断之前有没有存储pre-k这种前缀和,如果有,说明pre-k到pre直接的那些元素值之和就是k
for(inti=0;i< nums.length; i++) {
//存储索引为i的这个元素时,前缀和的值是多少
pre+=nums[i];
//判断之前有没有存储pre-k这种前缀和
if(mp.containsKey(pre-k)){
//如果有,说明pre-k到pre直接的那些元素值之和就是k
//找到了一组,累加到count上
count+=mp.get(pre-k);
}
//这个值出现的频次存储到mp中
// getOrDefault:当 Map 集合中有这个 key 时,就使用这个 key 对应的 value 值
//如果没有就使用默认值defaultValue
mp.put(pre,mp.getOrDefault(pre,0)+1);
}
//返回结果
returncount;
}
}
2、C++ 代码
classSolution{
public:
intsubarraySum(vector<int>&nums,intk){
//统计和为K的子数组的数量
intcount=0;
//记录遍历到索引为i的这个元素时,前缀和的值是多少
intpre=0;
//利用哈希表,以前缀和为键,出现次数为对应的值,记录pre[i]出现的次数
unordered_map<int,int>mp;
//一开始,需要设置前缀和为0时,出现的次数为1次
//这一行的作用就是为了应对nums[0]+nums[1]+...+nums[i]==k这种情况
//如数组[1,2,3,6]
//这个数组的累加和数组为[1,3,【6】,12]
//如果k=6,假如mp中没有预先存储(0,1)
//那么来到累加和为6的位置时,这时mp中存储的就只有两个数据(1,1),(3,1)
//想去判断mp.containsKey(pre-k),这时pre-k=6-6=0
//但map中没有(0,1),
//因为这个时候忽略了从下标0累加到下标i等于k的情况
//仅仅是统计了从下标大于0到某个位置等于k的所有答案
mp[0]=1;
//开始从头到尾遍历nums数组,在遍历过程中,会执行两个操作
//1、存储索引为i的这个元素时,前缀和的值是多少,并且把这个值出现的频次存储到mp中
//2、判断之前有没有存储pre-k这种前缀和,如果有,说明pre-k到pre直接的那些元素值之和就是k
for(inti=0;i< nums.size(); i++) {
//存储索引为i的这个元素时,前缀和的值是多少
pre+=nums[i];
//判断之前有没有存储pre-k这种前缀和
if(mp.find(pre-k)!=mp.end()){
//如果有,说明pre-k到pre直接的那些元素值之和就是k
//找到了一组,累加到count上
count+=mp[pre-k];
}
//这个值出现的频次存储到mp中
mp[pre]++;
}
//返回结果
returncount;
}
};
3、Python 代码
classSolution:
defsubarraySum(self,nums:List[int],k:int)->int:
#统计和为K的子数组的数量
count=0
#记录遍历到索引为i的这个元素时,前缀和的值是多少
pre=0
#利用哈希表,以前缀和为键,出现次数为对应的值,记录pre[i]出现的次数
mp=collections.defaultdict(int)
#一开始,需要设置前缀和为0时,出现的次数为1次
#这一行的作用就是为了应对nums[0]+nums[1]+...+nums[i]==k这种情况
#如数组[1,2,3,6]
#这个数组的累加和数组为[1,3,【6】,12]
#如果k=6,假如mp中没有预先存储(0,1)
#那么来到累加和为6的位置时,这时mp中存储的就只有两个数据(1,1),(3,1)
#想去判断mp.containsKey(pre-k),这时pre-k=6-6=0
#但map中没有(0,1),
#因为这个时候忽略了从下标0累加到下标i等于k的情况
#仅仅是统计了从下标大于0到某个位置等于k的所有答案
mp[0]=1
#开始从头到尾遍历nums数组,在遍历过程中,会执行两个操作
#1、存储索引为i的这个元素时,前缀和的值是多少,并且把这个值出现的频次存储到mp中
#2、判断之前有没有存储pre-k这种前缀和,如果有,说明pre-k到pre直接的那些元素值之和就是k
foriinrange(len(nums)):
#存储索引为i的这个元素时,前缀和的值是多少
pre+=nums[i]
#判断之前有没有存储pre-k这种前缀和
#如果有,说明pre-k到pre直接的那些元素值之和就是k
#找到了一组,累加到count上
#利用defaultdict的特性,当presum-k不存在时,返回的是0
count+=mp[pre-k]
#这个值出现的频次存储到mp中
# getOrDefault:当 Map 集合中有这个 key 时,就使用这个 key 对应的 value 值
#如果没有就使用默认值defaultValue
mp[pre]+=1
#返回结果
returncount
四、复杂度分析
时间复杂度:O(n),其中 n 为数组的长度。我们遍历数组的时间复杂度为 O(n),中间利用哈希表查询删除的复杂度均为 O(1),因此总时间复杂度为 O(n)。
空间复杂度:O(n),其中 n 为数组的长度。哈希表在最坏情况下可能有 n 个不同的键值,因此需要 O(n) 的空间复杂度。
审核编辑 :李倩
-
数组
+关注
关注
1文章
417浏览量
26064 -
leetcode
+关注
关注
0文章
20浏览量
2354
原文标题:LeetCode 560:和为 K 的子数组
文章出处:【微信号:TheAlgorithm,微信公众号:算法与数据结构】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
MultiGABSE-AU物理层PMA子层及PMD子层的相关机制
数组的下标为什么可以是负数
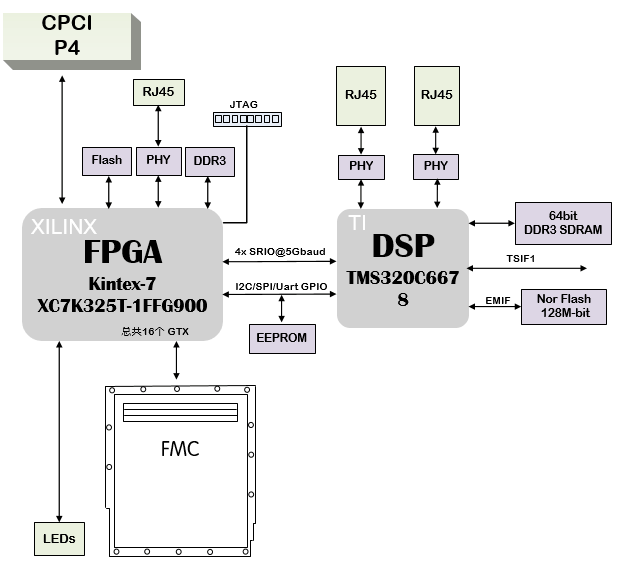
FMC子卡设计方案:202-基于TI DSP TMS320C6678、Xilinx K7 FPGA XC7K325T的高速数据处理核心板
指针数组和二维数组有没有区别
labview字符串数组转化为数值数组
使用stm32l451片子,对ad7606进行3通道100k采样值跳动问题?
面试常考+1:函数指针与指针函数、数组指针与指针数组





 LeetCode 560:和为K的子数组
LeetCode 560:和为K的子数组











评论