谈谈隔振器的选择

在这篇文章中，我们来谈谈隔振器的选择。显而易见，我们遇到的第一个问题将会是隔振器（vibration isolator）的定义。在经典的课本中，通常都是用质量和弹簧系统表示的。为了更形象的解释其作用，让我们先来举一些例子：我们知道汽车发动机运行时，会产生很高的振动。那如何避免这些振动传递到车架和座椅上呢？实际上，可以将隔振器（悬置）安装在发动机与车身的连接位置。这些隔振器的主要目的是为了避免发动机产生的振动传递到汽车的底盘，进一步传递到车内座椅上，从而避免汽车结构部件的疲劳失效以及噪音辐射。

再来举一个例子。设想我们需要在地铁的旁边建造一栋大楼，当地铁运行时，铁轨会有很大的振动。这些振动能量很容易传递到大楼，从而造成楼内人员的不适。于此同时，大楼的振动还可能造成其关键结构的疲劳失效，从而危害建筑安全。那我们又如何减少大楼的振动呢？一个常规的方法是在大楼基角下面安装隔振器，以切断或减弱振动能量的传递路径（transmission path）。所以说，隔振器的目的就是为了切断或减弱振动能量的传递。

那我们如何来选择隔振器呢？经典的隔振器设计方法是将整个系统假设为单自由度系统（SDOF system）。这个单自由度系统的刚度是由隔振器的弹性体提供，因为其刚度远远小于其他物理结构。与此同时，这个系统的质量一般是选取振动源和被隔振结构中较小的那一个。我们就回到刚才举的那两个例子：在发动机悬置的例子中，汽车发动机的质量远小于汽车车身和底盘的质量，所以将发动机作为这个单自由度系统的质量。在大楼的例子而言，大楼的质量将远小于大地的质量，所以将大楼作为这个单自由度系统的质量。当我们知道这个系统的刚度和质量后，可以很容易地计算得到这个系统的固有频率。

对于这个单自由度系统，可以很容易的获得振动传递率（transmissibility）曲线。关于它的介绍，在这篇文章里就不赘述，感兴趣的朋友可以参考清华大学出版社的《振动理论及应用》或是科学出版社的《机械振动和噪声学》。在通常情况下，单自由度的传递曲线如下图所示，纵轴代表振动传递率，横轴表示频率比（激励频率与固有频率之比）。振动传递率越低，该隔振器效果越好。

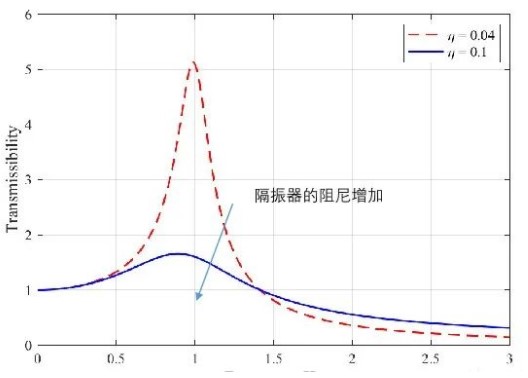
对于单自由度系统的传递曲线，以下几个特性尤为重要，为了便于理解，还是通过汽车隔振器的例子加以说明：

当汽车发动机发生刚体运动时，隔振器完全不工作。这是由于发动机和车架没有发生往复性运动，惯性力不参与他们的能量交换，只存在静态力的传递 。

当发动机的激励频率低于固有频率的1.4倍时，车架上的振动将会比发动机的振动更高。反之，隔振器将减弱振动的传递。

当发动机激励频率低于系统固有频率的1.4倍，增加阻尼将会降低振动传递率。反之，阻尼将会使隔振效果下降。

通常情况下，一个最重要的隔振器的设计准则是其固有频率需要远远低于振动源设备的最低激励频率。在这种情况下，增加阻尼将会降低隔振器的性能。那为什么大部分隔振器还是设计了一定的阻尼？这是因为当汽车发动机启动时，发动机的速度总是从零达到额定的速度。在这个过程中，隔振器系统的固有频率对应的模态总会被激励，这将会对于车架造成一定的冲击。我们可以看到，在系统固有频率处，增加隔振器阻尼1.5倍将会降低振动传递率（至少五倍）。而在高频时，隔振器传递率只有有限的增加。所以，在隔振器设计之中，我们还是需要保证一定的阻尼。

从这条单自由度的隔振曲线，可以看出，当隔振器系统的固有频率远远小于激励频率时，隔振器的效果将会提升。理论上而言，我们需要选择最软的隔振器。但是在实际应用中，隔振器还有一个重要的限制。那就是最大静态载荷。那静态载荷又是如何影响隔振器的性能的呢？我们可以从下面两个方面来看。

首先，当静态载荷过大时，隔振器被过度挤压，振动源设备可能会直接与其他元件相接触。因为接触所产生的刚度远远高于隔振器的刚度，所以隔振器将会被绕过，振动可以通过金属接触而直接传递到振动敏感结构上。

其次，隔振器的刚度也并非完全线性，特别是对于橡胶隔振器。当隔振器被过度挤压后，橡胶几何结构的变形将会明显提升橡胶的刚度，系统的固有频率将会出乎意料的提升。这对于隔振器设计也是致命的。

从这个公式中，我们可以看到，系统的固有频率和静态形变成反比。所以，一个最重要的隔振器选择的经验法则就是：在静态形变要求可以满足的情况下，尽可能寻找较软的隔振器。在这种情况下，隔振效果会最佳。

在实际工程应用中，经常会发现单自由度隔振理论所估计的隔振效率无法达到，一个重要的原因是隔振器支撑结构的刚度不足。这是一个很有趣但又经常出现的问题。我们前面所提及的分析都是基于单自由度系统。一个很重要的假设就是，隔振器的支撑结构一般为刚体。在实际的工程问题中，隔振器往往放在一个弹性体上，例如在汽车发动机悬置（engine mount）往往是放置于副车架之上。在这种情况下，被隔振的部件就无法继续假设为单自由度的系统下。

对于这种情况，隔振系统就可以简化为下图所示的离散化的模型。

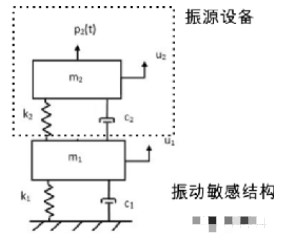
为了更好的说明原因，我们继续使用发动机隔振器的例子。对于这个结构，振源设备是发动机，而振动敏感结构是车架。从上图可以看出，我们可以把车架简化为了一个由车架的总质量和抗弯刚度组成的单自由度系统。与此同时，我们假设车架的阻尼可以忽略。对于这个二自由度系统，一个典型的振动传递曲线如下图所示：

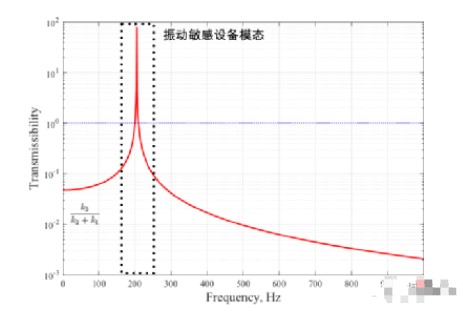
在这个设计之中，隔振器系统的固有频率在10Hz左右，而车架的固有频率在200Hz。我们可以看到，隔振器在车架的频率处完全失效，振动传递系数远高于1。这和传统的隔振器设计理论时相悖的。

那么，我们又如何在非刚体车架上设计隔振器呢？为了研究这个问题，我们先来做一些灵敏度分析。首先，我们可以观察车架的刚度会如何影响传递率曲线。

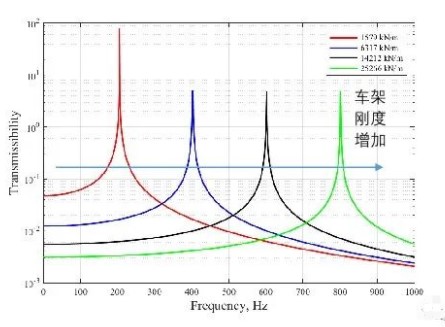
可以看到，当发动机的激励频率远离车架的固有频率时，随着车架刚度增加，隔振器的传递率将会降低。在车架的固有频率处，这种关系并不是特别的明确（下图显示了振动敏感结构刚度和在其固有频率的传递率的关系）。不过，我们可以看到，在这些频率处，隔振传递率永远是高于1。换句话说，车架的振动将会高于发动机的振动。

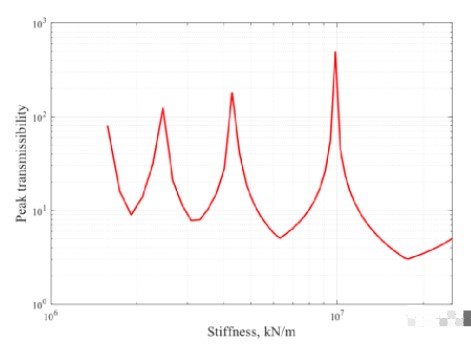
如果我们改变隔振器系统的固有频率，隔振传递率又将会如何变化呢？可以参考下图。为了简化整体的分析，我们假设隔振器的自然频率远低于车架的自然频率。

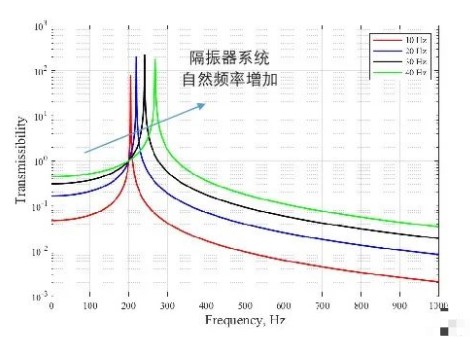
我们可以看到，随着隔振器系统固有频率靠近车架的固有频率，隔振器的传递率将逐渐变高，隔振器效果逐渐变差。这和传统隔振器设计准则保持一致。

所以说，当我们设计隔振器的时候，我们需要在保证最大静态载荷的要求下，尽量将隔振器的刚度变低。与此同时，在支撑隔振器的位置，支撑隔振器结构的固有频率需要远高于最高的激振频率，这样才能保证隔振器的正常工作。



审核编辑：刘清