张正友标定算法是什么意思

”张正友标定”是指张正友教授1998年提出的单平面棋盘格的摄像机标定方法。文中提出的方法介于传统标定法和自标定法之间，但克服了传统标定法需要的高精度标定物的缺点，而仅需使用一个打印出来的棋盘格就可以。同时也相对于自标定而言，提高了精度，便于操作。因此张氏标定法被广泛应用于计算机视觉方面。

原理

1.计算外参

设三维世界坐标的点为M=[X,Y,Z,1]T，二维相机平面像素坐标为m=[u,v,1]T，所以标定用的棋盘格平面到图像平面的单应性关系为：sm=A[R,t]M
其中

不妨设棋盘格位于Z = 0，定义旋转矩阵R的第i列为 ri, 则有：

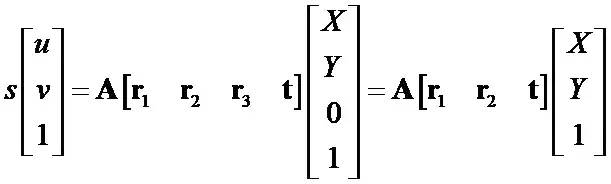
令H=[h1 h2 h3]=λA[r1 r2 t]

于是空间到图像的映射可改为：sm=HM，

其中H是描述Homographic矩阵，H是一个齐次矩阵，所以有8个未知数，至少需要8个方程，每对对应点能提供两个方程，所以至少需要四个对应点，就可以算出世界平面到图像平面的单应性矩阵H

外参具体计算公式。注意：R3是 t

一般而言，求解出的R = [r1 r2 t] 不会满足正交与归一的标准

在实际操作中，R 可以通过SVD分解实现规范化(详见原文)

2.计算内参

由r1和r2正交，且r1和r2的模相等，可以得到如下约束：

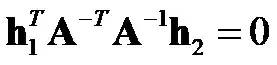
正交

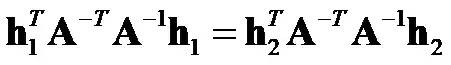
模相等

可以推到出

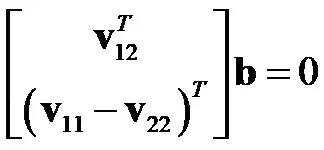
根据推到的结果可知如果有n组观察图像，则V 是 2n x 6 的矩阵

根据最小二乘定义，V b = 0 的解是 VTV 最小特征值对应的特征向量。

因此, 可以直接估算出 b，后续可以通过b求解内参

因为B中的未知量为6个，

所以当观测平面 n ≥ 3 时，可以得到b的唯一解

当 n = 2时, 一般可令畸变参数γ = 0

当 n = 1时, 仅能估算出α 与 β, 此时一般可假定像主点坐标 u0 与 v0 为0

内部参数可通过如下公式计算(cholesky分解)：

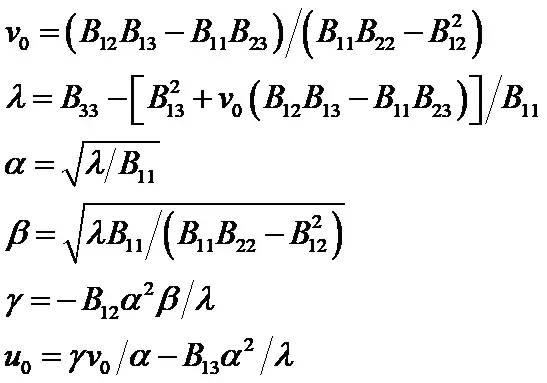
内参具体计算公式

3.最大似然估计

上述的推导结果是基于理想情况下的解，但由于可能存在高斯噪声，所以使用最大似然估计进行优化。设我们采集了n副包含棋盘格的图像进行定标，每个图像里有棋盘格角点m个。令第i副图像上的角点Mj在上述计算得到的摄像机矩阵下图像上的投影点为：

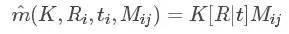
这里的K为相机内参矩阵A

其中Ri和ti是第i副图对应的旋转矩阵和平移向量，K是内参数矩阵。则角点mij的概率密度函数为：

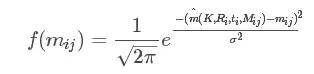
这里的K为相机内参矩阵A

构造似然函数：

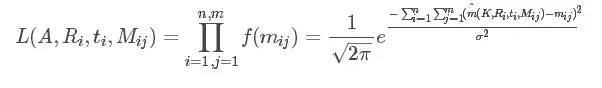
这里的K为相机内参矩阵A

让L取得最大值，即让下面式子最小。这里使用的是多参数非线性系统优化问题的Levenberg-Marquardt算法[2]进行迭代求最优解。

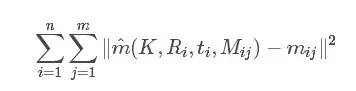
这里的K为相机内参矩阵A

4.径向畸变估计

张氏标定法只关注了影响最大的径向畸变。则数学表达式为：

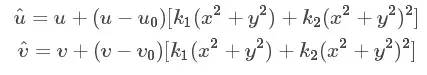
其中，(u,v)是理想无畸变的像素坐标，(u,v)(u,v)是实际畸变后的像素坐标。(u0,v0)代表主点，(x,y)是理想无畸变的连续图像坐标，(x,y)(x,y)是实际畸变后的连续图像坐标。k1和k2为前两阶的畸变参数。

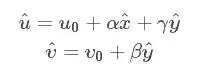
化作矩阵形式：

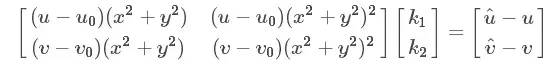
记做：Dk=d

则可得：

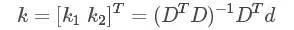
计算得到畸变系数k。

使用最大似然的思想优化得到的结果，即像上一步一样，LM法计算下列函数值最小的参数值：

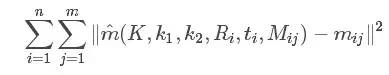
这里的K为相机内参矩阵A

到此，张氏标定法介绍完毕。我们也得到了相机内参、外参和畸变系数。

相机标定步骤

打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上

针对棋盘格拍摄若干张图片（一般10-20张）

在图片中检测特征点（Harris特征）

利用解析解估算方法计算出5个内部参数，以及6个外部参数

根据极大似然估计策略，设计优化目标并实现参数的refinement。

审核编辑：刘清