算法之空间复杂度:衡量一个算法运行需要开辟的额外空间
上次我们学习了时间复杂度,那么我们今天就来看看空间复杂度!
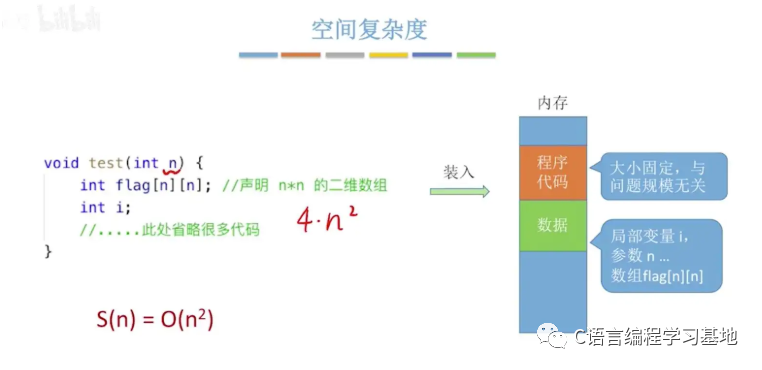
概念
空间复杂度是对一个算法在运行过程中临时占用空间大小的度量
和时间复杂度不是真的计算时间一样,空间复杂度也不衡量算法具体占用的内存字节数。
空间复杂度计算的是额外开辟的变量的个数,适用大O渐近法
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
空间复杂度计算
NO.1 冒泡排序
voidBubbleSort(int*a,intn){assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}}
我们会发现,冒泡排序算法并没有额外定义非常多的变量,一共只有3个,属于常数阶
size_t end = n;int exchange = 0;size_t i = 1;
其空间复杂度为O(1)
计算时注意其与N的关系
当我们在算法中开辟空间,计算空间复杂度的时候,要注意开辟的这个空间与N有没有关系
int arr[N];//c99变长数组,和传过来的参数有关int*a=(int*)malloc(sizeof(int)*N);//和传过来的参数有关,O(N)int* a=(int*)malloc(sizeof(int)*3);//和传过来的参数无关,O(1)
NO.2 斐波那契数列
// 计算Fibonacci的空间复杂度?// 返回斐波那契数列的前n项long long* Fibonacci(size_t n){if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;}
和上面的斐波那契数列的递归代码不同,这里我们新创建了一个数组,用来保存计算出来的斐波那契数
一共malloc了n+1个长整型的空间,空间复杂度是O(N)
空间重复使用问题
如果是递归方法的斐波那契算法,其空间复杂度是多少呢?
long long Fib(size_t N){if(N < 3)return 1;return Fib(N-1) + Fib(N-2);}
答案也是O(N)
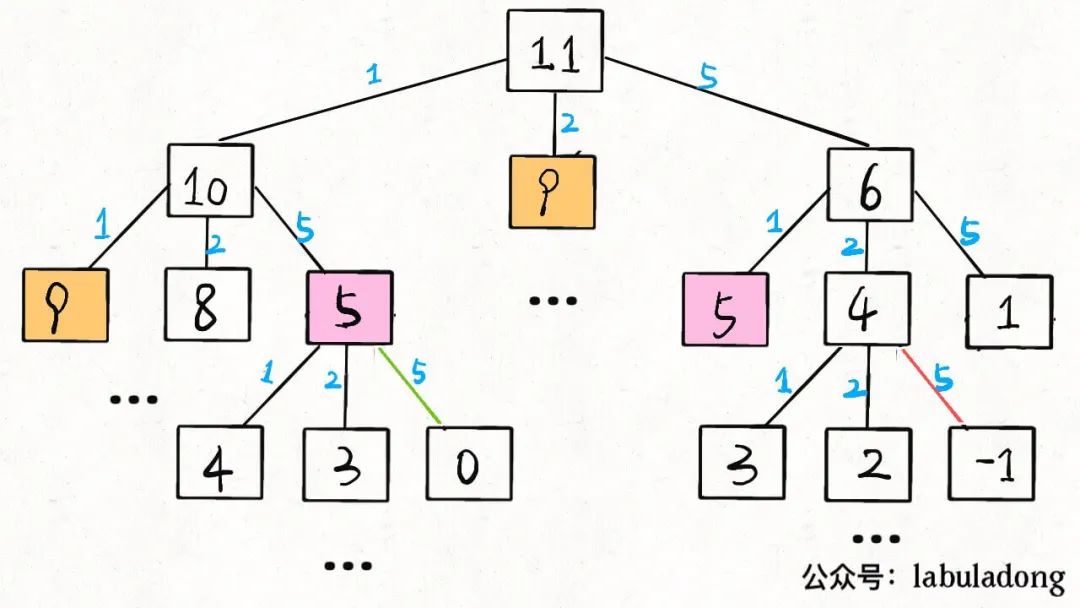
因为对于递归算法而言,其开辟的函数栈帧空间是可以重复利用的!
如fib(8)的调用,其开辟的函数栈帧,是可以在后续继续调用fib函数时重复使用的
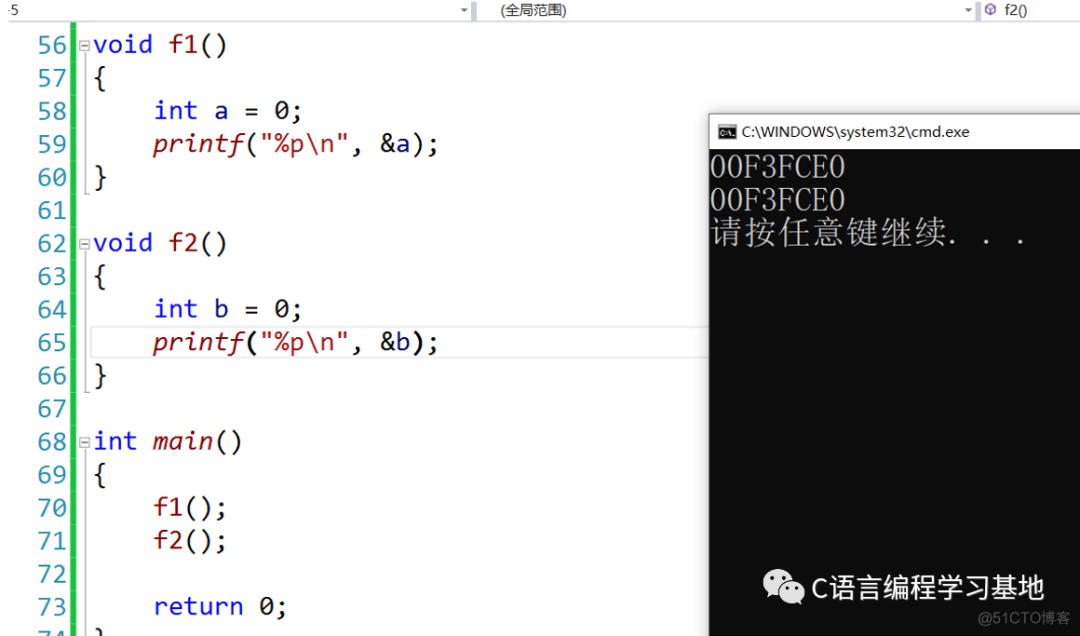
上图中f1和f2是两个函数,但执行了相同的功能。其函数调用的空间实际上是一个,f2在f1销毁后继承了它的空间
这就好比每一次新的递归都会开一家新的饭店,但是你下次还想吃东北菜的时候,可以去之前开的东北菜馆,咱没必要让别人再开一家馆子不是嘛?
不过由于斐波那契数的递归算法会递归非常多次,在数字很大的时候,会导致栈溢出
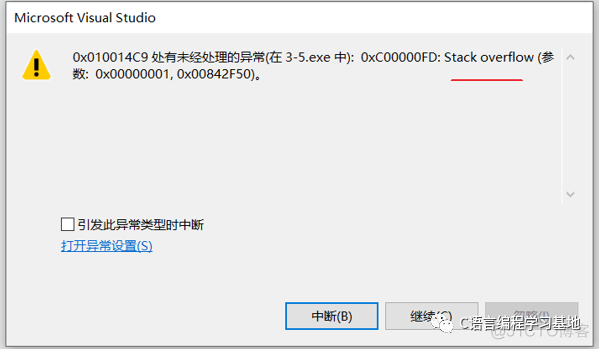
NO.3 阶乘
long long Fac(size_t N){if(N == 0)return 1;return Fac(N-1)*N;}
虽然函数本身的空间不计入时间复杂度,这里计算的是递归调用时额外开辟的函数栈帧空间
一共调用了N-1次,每个栈帧使用了常数个空间,空间复杂度是O(N)
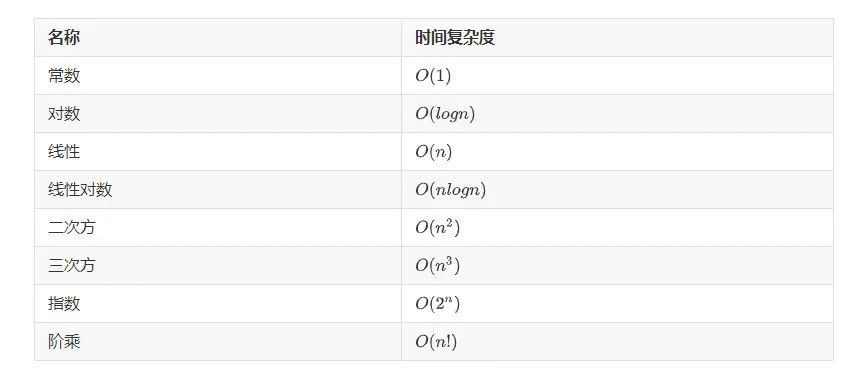
常见复杂度对比
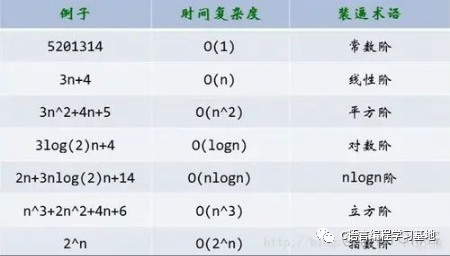
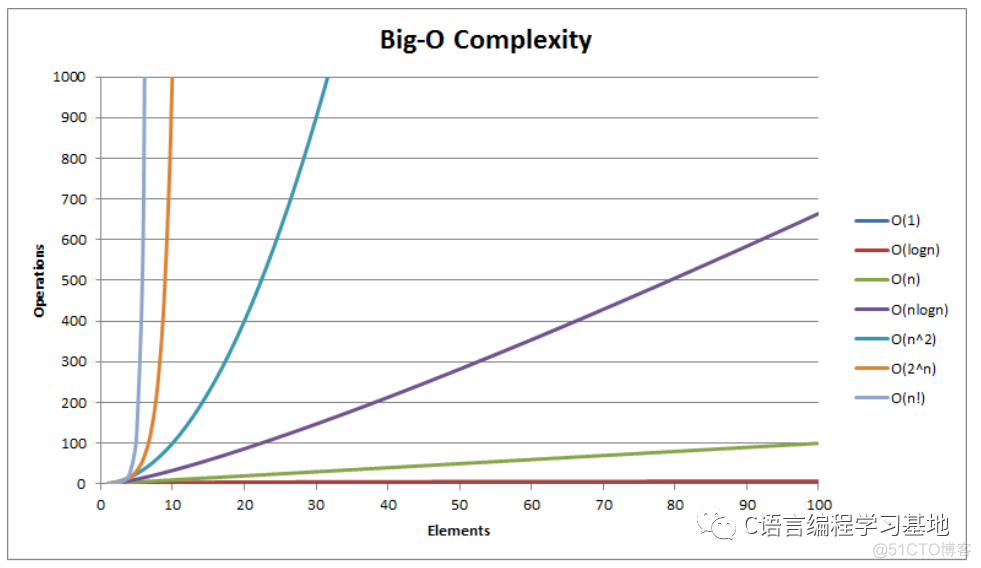
结语
时间复杂度和空间复杂度可以帮我们很好的了解自己所写算法的好坏,在未来面试的时候,HR肯定也更喜欢效率高的算法
要多刷题,好好积累自己的能力,想必之后写出好算法也是水到渠成(吧?)
-
算法
+关注
关注
23文章
4608浏览量
92852 -
计算
+关注
关注
2文章
449浏览量
38793 -
复杂度
+关注
关注
0文章
8浏览量
7901
原文标题:【算法】几分钟时间让你彻底学会—空间复杂度!
文章出处:【微信号:cyuyanxuexi,微信公众号:C语言编程学习基地】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
基于纹理复杂度的快速帧内预测算法
时间复杂度是指什么
LDPC码低复杂度译码算法研究

图像复杂度对信息隐藏性能影响分析
虚拟MIMO中低复杂度功率分配算法
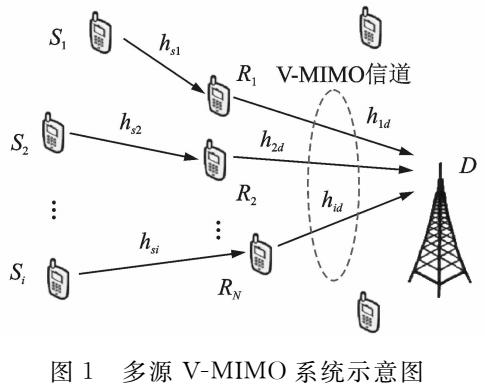
算法是什么?python的时间,空间复杂度和常用算法实例说明免费下载
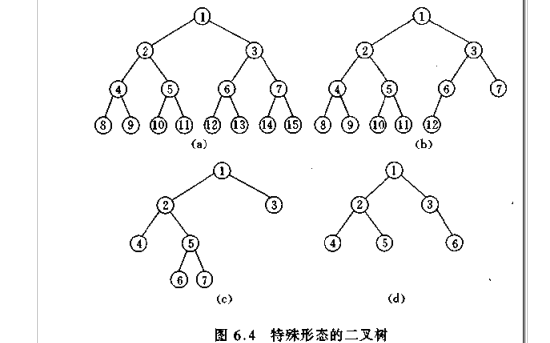
如何求递归算法的时间复杂度
常见机器学习算法的计算复杂度
算法时空复杂度分析实用指南2
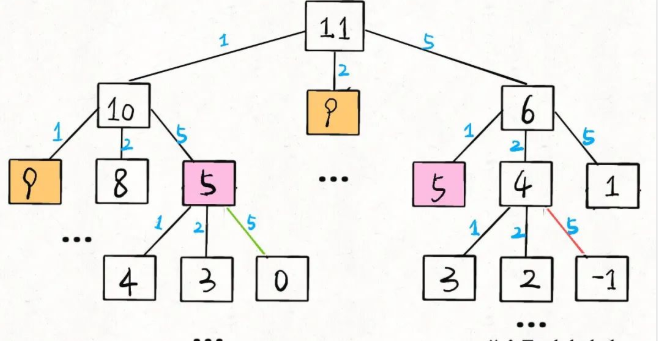
算法时空复杂度分析实用指南(上)




 算法之空间复杂度
算法之空间复杂度










评论