基于RFD的分层标签分配（HLA）模块设计

前言 在本文中，作者提出了一种基于高斯感受野的标签分配（RFLA）策略用于微小目标检测。并提出了一种新的感受野距离（RFD）来直接测量高斯感受野和地面真值之间的相似性，而不是使用IoU或中心采样策略分配样本。

考虑到基于IoU阈值和中心采样策略对大对象的倾斜，作者进一步设计了基于RFD的分层标签分配（HLA）模块，以实现小对象的平衡学习。在四个数据集上的大量实验证明了所提方法的有效性。作者的方法在AI-TOD数据集上的AP点数为4.0，优于SOTA。

创新思路

微小物体的像素数量极为有限（小于AI-TOD［49］中定义的16×16像素），一直是计算机视觉领域的一个难题。微小目标检测（TOD）是最具挑战性的方法之一，一般的物体检测器通常无法在TOD任务中提供令人满意的结果，这是由于微小物体缺乏鉴别特征。

考虑到微小物体的特殊性，提出了几种定制的TOD基准（如AI-TOD、TinyPerson和AI-TOT-v2），以促进一系列下游任务，包括驾驶辅助、交通管理和海上救援。最近，TOD逐渐成为一个受欢迎但具有挑战性的方向，独立于一般对象检测。

在本文中，作者认为当前的先验盒和点及其相应的测量策略对于微小物体是次优的，这将进一步阻碍标签分配过程。具体来说，作者以单个先验盒和点为例，从分布的角度重新思考它们。

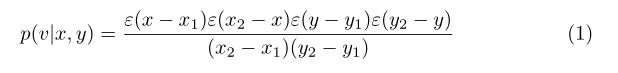
不同先验的示意图如图1的第二行所示，现有先验信息与其相应的测量策略相结合，对于微小物体存在以下问题。

图1.不同标签分配方案的检测结果之间的比较

第一：当特定ground truth与特定先验不重叠时，它们的位置关系无法通过IoU或中心度解决。对于微小对象，通常情况下，真实框与几乎所有的锚框都没有重叠（即IoU=0）或不包含任何锚定点，导致微小对象缺少正样本。

为此，采用启发式方法来保证微小对象的更多正样本。然而，赋值器通常无法基于零值IoU或中心度补偿微小对象的正样本。因此，网络将减少对微小对象学习的关注。

第二，当前先验区域主要遵循均匀分布，并同等对待先验区域内的每个位置。然而，基本上利用先验信息来辅助标签分配或特征点分配过程。

当将特征点的感受野重新映射回输入图像时，有效感受野实际上是高斯分布的。均匀分布先验和高斯分布感受野之间的间隙将导致ground truth和分配给它的特征点的感受野之间不匹配。

为了缓解上述问题，作者引入了一种新的基于高斯分布的先验知识，并建立了一种基于高斯感受野的标签分配（RFLA）策略，该策略更有利于微小对象。

本文的主要贡献

（1）实验表明，当前基于锚和无锚的检测器在微小目标标签分配中存在尺度样本不平衡问题。

（2） 为了缓解上述问题，引入了一种简单但有效的基于感受野的标签分配（RFLA）策略。RFLA很容易取代主流检测器中的标准盒和基于点的标签分配策略，提高了它们在TOD上的性能。

（3） 在四个数据集上的大量实验验证了提出的方法的性能优越性。在具有挑战性的AI-TOD数据集上，引入的方法在推理阶段没有额外成本的情况下显著优于最先进的竞争对手。

方法

感受野建模

基于锚的检测器在FPN的不同层上平铺不同尺度的先验框，以辅助标签分配，因此在FPN不同层上检测不同尺度的对象。对于无锚探测器，它们将不同比例范围内的对象分组到不同水平的FPN上进行检测。尽管标签分配策略各不相同，但基于锚和无锚检测器的一个共同点是将适当感受野的特征点分配给不同尺度的对象。

因此，在不设计启发式锚框预设或规模分组的情况下，感受野可以直接用作标签分配的有根据和有说服力的先验。

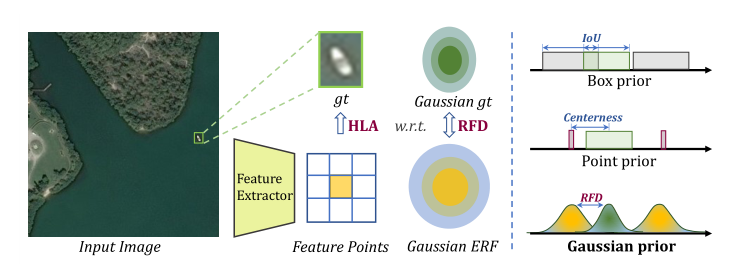
图2.RFLA的过程

在本文中，作者直接测量有效感受野（ERF）和ground truth区域之间的匹配度，以进行标记分配，从而消除使TOD恶化的盒或点先验。在这项工作中，将每个特征点的ERF建模为高斯分布，先通过以下公式推导出标准卷积神经网络上第n层的理论感受野（TRF），即trn：

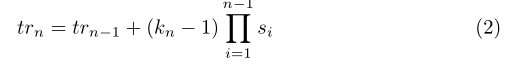
感受野距离

获得高斯ERF，关键步骤是测量特征点的ERF与某个ground truth之间的匹配度。阶跃变化的均匀分布不利于ground truth体，还需要将真实值建模为另一个分布。

观察到物体的主体聚集在边界框的中心，作者还将ground truth框（xg、yg、wg、hg）建模为标准的二维高斯分布Ng（µg，∑g），其中每个带注释框的中心点用作高斯的平均向量，半边长的平方用作协方差矩阵，即，

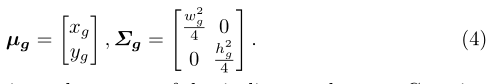
在本文中，作者研究了高斯分布之间的三种典型距离作为感受野距离候选（RFDC）。这些距离测量包括Wasserstein距离、K-L散度和J-S散度。高斯分布之间的J-S散度没有闭式解，在近似其解时将引入大量计算，因此，不使用J-S散度。

Wasserstein距离

Wasserstein距离来自最优运输理论。Wasserstein距离的主要优点是它可以测量两个非重叠分布。通常情况下，ground truth框与大多数在先框和点没有重叠，并且赋值器无法将这些候选ground truth级排序到某个真实值。

因此，可以很容易地说，Wasserstein距离的特性有利于TOD，TOD可以一致地反映所有特征点与某个ground truth盒之间的匹配程度，使赋值器能够根据合理的优先级对微小对象补偿更多的正样本。然而，Wasserstein距离不是尺度不变的，当数据集包含大尺度方差的对象时，它可能是次优的。

Kullback-Leibler散度

Kullback-Leibler散度（KLD）是一种经典的统计距离，用于衡量一种概率分布与另一种概率的差异。KLD在两个二维高斯分布之间具有尺度不变性，并且尺度不变性对检测至关重要。而KLD的主要缺点是，当两个分布的重叠可以忽略时，它不能一致地反映两个分布之间的距离。

因此，本文选择ERF和ground truth之间的KLD作为另一个RFDC。

然后，作者将非线性变换应用于RFDC，并得到归一化值范围在（0，1）之间的RFD，如下所示：

分层标签分配

作者通过分数排序将标签分层分配给微小对象。为了保证任何特征点和任何ground truth之间的位置关系都可以求解，所提出的分层标签分配（HLA）策略建立在所提出的RFD之上。在分配之前，基于ground truth计算特征点和真实值之间的RFD ground truth。

在第一阶段，作者使用特定的真实值对每个特征点的RFD得分进行排序。然后，将ground truth配给具有最高k个RFD分数的特征点，并具有一定的ground truth。最后，得到分配结果r1和已分配特征的对应掩码m。

在第二阶段，为了提高整体召回率并缓解异常值，通过乘以阶段因子β来略微衰减有效半径ern，然后重复上述排序策略，并向每个ground truth补充一个正样本，得到分配结果r2。通过以下规则获得最终分配结果r：

探测器的应用

所提出的RFLA策略可以应用于基于锚和无锚的框架。为了更快的R-CNN，RFLA可以用来代替标准的锚平铺和MaxIoU锚分配过程。对于FCOS，消除了限制ground truth框内特征点的限制，因为小框只覆盖非常有限的区域，通常比大对象包含的特征点少得多。

用RFLA代替基于点的分配，实现平衡学习。

作者将中心度损失修改为以下公式，以避免梯度爆炸：

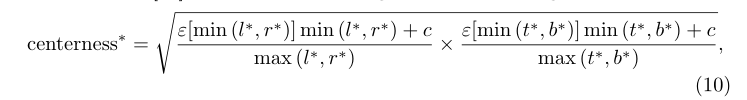
实验

如表1所示，可以看出，GIoU不如RFD，因为它无法区分相互包容的盒子的位置，而WD和KLD的性能相当。

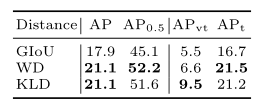
表1.不同感受野距离测量方法的比较

作者逐步将RFD和HLA应用到更快的RCNN中。结果列于表2，AP逐步改善，从而验证了个体有效性。

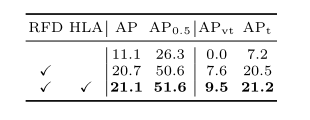
表2.不同设计的影响

在HLA中，作者为ERF设计了阶段因子β，以缓解异常值效应。在表3中，作者保持所有其他参数不变，实验表明0.9是最佳选择。将β设置为较低的值将引入太多的低质量样本。

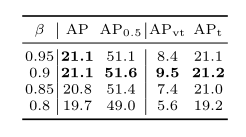
表3.分级标记赋值器（HLA）中阶段因子β的影响

作者将锚直接建模为高斯分布，计算ground truth之间的RFD得分，然后使用HLA分配标签。结果如表4所示。结果表明高斯先验及其与HLA的结合具有很大的优势。

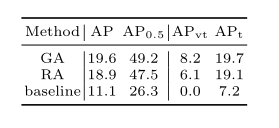
表4.高斯锚和接受锚

作者将作者的方法与AI-TOD基准上的其他最先进检测器进行了比较。如表5所示，带RFLA的探测器达到24.8 AP，比最先进的竞争对手高出4.0 AP。

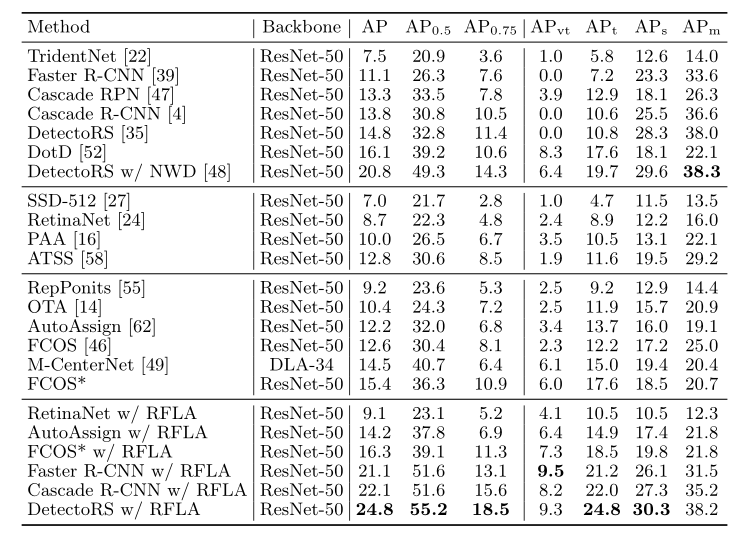
表5.AI-TOD的主要结果

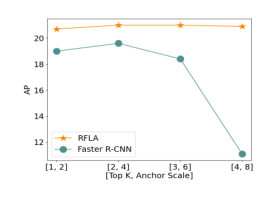
图3.快速R-CNN w/HLA中的top k与快速R-CNN基线中的锚定微调之间的比较

作者将标度范围划分为16个区间，如图4所示，并计算分配给不同标度范围中每个ground truth的正样本的平均数量。图4中的观察结果表明现有检测器存在严重的标度样本不平衡问题。

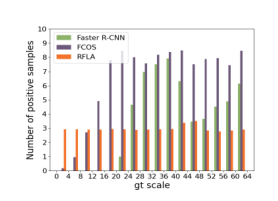
图4.不同检测器的比例样本不平衡问题

AI-TOD数据集的可视化结果如图5所示。当将RFLA应用于更快的R-CNN时，可以大大消除FN预测。

图5.AI-TOD的可视化结果

结论

在本文中，作者指出框和点先验对于TOD不起作用，导致在分配标签时出现比例样本不平衡问题。为此，作者引入了一种新的高斯感受野先验。

然后，作者进一步设计了一种新的感受野距离（RFD），它度量了ERF和ground truth之间的相似性，以克服TOD上IoU和中心性的不足。RFD与HLA策略一起工作，为微小对象获得平衡学习。

在四个数据集上的实验表明了RFLA的优越性和鲁棒性。

审核编辑：彭静