浅析光具有的三种动量

在中学物理中，我们就接触过动量（Momentum）这一概念。一个运动物体所具有的动量等于该物体的质量乘以它的速度。当两个物体发生弹性碰撞时，动量可以在二者之间转移。比如在打台球时，用白色主球撞击其他球的过程，也就是将白色主球的部分或者全部动量转移给其他球的过程。

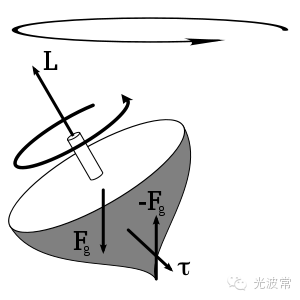
当一个物体围绕着某个轴转动时，该物体还具有角动量（Angular momentum）。角动量的大小正比于物体的质量、转动的速度以及物体到轴的距离；角动量是个矢量，其方向垂直于物体转动的平面。在没有外加力矩（或者总体外加力矩为零）的情况下，物体的角动量大小和方向保持不变。利用了角动量大小守恒这一原理，花样滑冰选手在做旋转动作时，可以将双臂抱紧以减小身体到旋转轴的有效距离从而增加旋转速度。角动量方向守恒在日常生活中更是有诸多应用，比如陀螺在高速旋转时能直立在地面上，子弹必须高速旋转才能准确击中目标，美式橄榄球传球时让球旋转等等。为了与角动量区分，在前面提到的、由质量与速度乘积定义的动量又被称为线性动量（Linear Momentum）。

(from wiki)

其实光也具有这三种动量：线性动量、自旋角动量和轨道角动量。如果一个兵乓球撞到镜子上，被弹开，由于线性动量的改变（主要是方向）导致在弹开瞬间对镜面产生压力。类似的，当照射在镜面上的光被镜子反射时，光的线性动量发生改变，从而对镜子产生一个压力（推力），这种压力也被称为辐射压力（Radiation pressure）。

光对被照射的物体施加辐射压力这一概念，最早由德国数学家和天文学家开普勒在1619年提出。当时人们发现彗星接近太阳时，总是拖着长长的尾巴（彗尾），而且尾巴总是出现在彗星背向太阳的一侧。开普勒认为是太阳光的辐射压力将彗星中很多尘埃颗粒推向彗星身后，从而在其背向太阳的一侧形成彗尾。

在中国传统文化中，彗星象征着不吉利。又因为看起来像个扫把，所以彗星在中国又被称为扫把星。哈雷彗星每76年光临一次地球。世界上公认的对哈雷彗星最早的记录，来源于《史记》。

1871年，电磁学集大成者麦克斯韦在理论上预言了辐射压力现象。辐射压力很小，将平均功率为5毫瓦的激光垂直入射到镜子表面，假定所有光被反射，那么镜面所感受到的压力只有33×10-12牛顿。毫无疑问，在200多年前测量如此小的力，是一件极具挑战性的工作。好在当时物理学界已经普遍采用扭秤（Torsion

balance）测量微小的力。这种方法最早由法国物理学家库仑在1777年发明。为了测量电荷之间的静电引力或斥力，库仑将一个绝缘横杆用细丝水平悬在空中，绝缘横杆的一端装有一个带电小球。由于电荷间引力或者斥力的作用，当另外一个带电小球在水平方向上靠近横杆末端的小球时，绝缘横杆会发生转动，转动的角度取决于力的大小。利用扭秤，库仑发现了著名的库仑定律：两个点电荷之间的作用力正比于二者电量乘积，反比于二者间距离的平方。1798年，英国科学家卡文迪许利用扭秤间接测量了万有引力常数（Gravitationa

constant）。

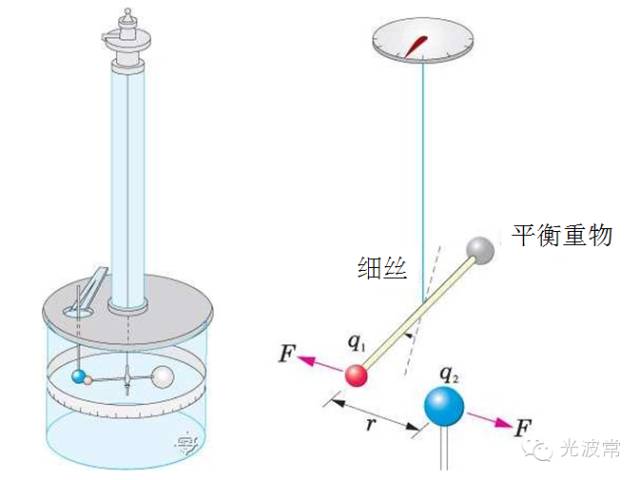
库仑扭秤 (Adapted from Wiki)

扭秤将力的测量转化为细丝扭转角度的测量。显然，这种方法的测量精度和灵敏度由细丝的力学性质决定，当时常用的材料包括头发、丝绸或者钨丝等等。英国实验物理学家Charles Vernon Boys，一直痴迷于建造能用于精确测量的各种实验装置。为了进一步改进扭秤，Boys测试了很多材料后想到了玻璃纤维（Glass fiber）。玻璃纤维的出现可以追溯到公元前1600年的埃及。到19世纪晚期，上好的玻璃纤维可以比蚕丝还要纤细，那时人们经常把不同颜色的玻璃纤维编织成布匹，用以各种装饰。1887年，Boys能找到的玻璃纤维最小直径为25微米，测试效果并不理想，表明需要采用更细的玻璃纤维。

当时获得玻璃纤维的办法，是将熔化后的细玻璃棒快速拉成细丝。因此要想获得更细的玻璃纤维，就要想办法提高在玻璃熔化后拉纤维的速度。为此,Boys制作了一把弩，然后将质量很轻的箭装在弩上，再将玻璃预制棒的一端固定在箭尾上。等预制棒被加热到1600摄氏度熔化后，箭被弩快速射出，后面就能拖出长长的玻璃纤维。利用这种办法，Boys可以轻松获得27米长、直径在2.5微米的玻璃纤维。借助石英（Quartz）玻璃纤维，Boys研制成辐射微热计（Radio micrometer）,能够测量到放在5公里之外的点燃的蜡烛所产生的热效应。

自此石英玻璃纤维成为制作扭秤装置的不二之选。利用这种扭秤，在1900年俄罗斯物理学家PyotrLebedev实验验证了由于光线性动量的改变而产生的辐射压力。

如果将光束聚焦，在焦点附近的物体的不同部分感受到来自不同方向上的光线，这些光线在物体表面既有反射又有折射，反射和折射改变光的线性动量，因此光对物体产生力的作用，由于光强在焦点附近是梯度分布从而对物体产生了梯度力（Gradient force）。如果物体很小（纳米到微米量级）很轻，它会被聚焦光束限制在焦点附近、合力为零的平衡位置。通过移动光束的焦点位置，被“抓住”的微小物体也会随之被移动。这种技术称为光镊子，最早于1970年由在贝尔实验室工作的Ashkin发明，随即被广泛应用于生物学研究，用于操作生物大分子或者细胞等。

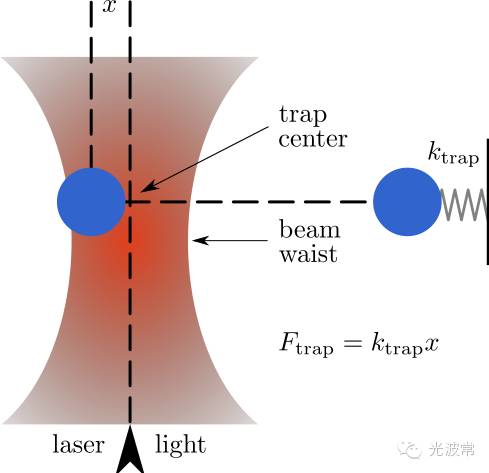
(from Wiki)

在用量子力学描述的世界中，物理学家用光子（Photon）来描述光和其他基本粒子的相互作用。对于一个光子，它的线性动量为普朗克常数除以波长。

光子当然也有自旋角动量。1909年，光子的概念尚未建立之前，英国物理学家John Poynting就提出圆偏振光具有角动量（实际上是自旋角动量），并且认为当光经过某个光学器件（比如波片）改变偏振态时，会伴随着角动量在光和器件之间的转移。1936年，Beth将一个半波片水平悬挂在石英玻璃纤维上制成扭秤，当右旋圆偏振光通过该波片转换为左旋圆偏振光时，光束自旋角动量的改变引起了波片转动。

该实验的测量结果验证了Poynting的猜想。现在我们知道，左（右）旋圆偏振的光子具有的自旋角动量为正（负）的普朗克常数除以2倍的圆周率。一个线偏振光，可以分解为幅度相等的两个旋转方向相反的圆偏振光的线性叠加，因此它的自旋角动量为零。

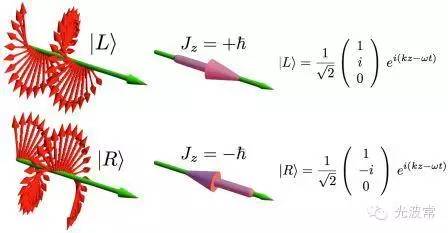
(Adapted from Wiki)

令人吃惊的是，直到1992年，物理学家们才意识到光也可以具有轨道角动量。众所周知，我们熟悉的高斯光束是旁轴波动方程（Paraxial wave equation）的厄米－高斯（Hermite-Gaussian）本征解中的最低阶模式HG00。其实旁轴波动方程还有另外一组完备的正交本征解，那就是不太被大家熟知的拉盖尔－高斯（Laguerre-Gaussian）模式，通常记为LG(p,n)。p和n分别取0，1，2，...整数，用来表示不同阶的模式，比如LG(0,0)对应的就是我们常见的高斯光束。对于n不为0的高阶拉盖尔－高斯光束，在光束的中心，光强为零，同时该光束的波前（Wave front）为螺旋状（Hellical），表征光束能量传输的Poynting矢量也沿着螺旋曲线（Spiral trajectory）前行。

1986年，Coullet意识到在数学上，这种具有螺旋波前的拉盖尔－高斯光束与流体力学中的涡旋具有相似之处，因此将前者命名为光涡旋（Optical votex）。1992年，荷兰莱顿大学的Allen等人意识到光涡旋携带有另外一种角动量－－轨道角动量。对于模式为LG(p,n)的拉盖尔－高斯光束来说，其中每个光子具有的轨道角动量为n乘以普朗克常数除以两倍的圆周率。

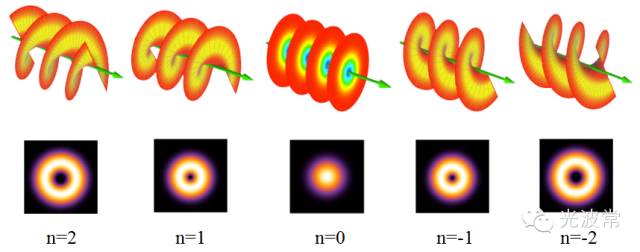
高阶拉盖尔－高斯光束的螺旋波前和光强分布

近年来，研究和利用光束的角动量俨然成为光学前沿之一。比如，利用圆偏振的高斯光束聚焦形成的光镊子不仅可以“抓住”微小物体，并且可以将光束本身的自旋角动量转移到微小物体上，从而对微小物体进行转动操作－－有人将这样的光学装置形象地称为光扳手（Optical spanner）。类似的光扳手也可以通过聚焦线性偏振的（自旋角动量为0）、n不为0的高阶拉盖尔－高斯光束来实现，只不过依靠的是光束本身的轨道角动量来转动微小物体。

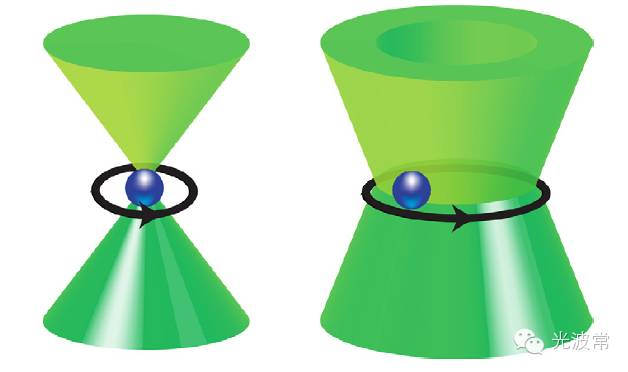
(Adapted from A.M. Yao and M. J. Padgett, “Orbital angularmomentum: origins, behavior and applications,” Advancesin Optics and Photonics 3, 161 (2011).)

审核编辑：刘清