1. 什么是平衡二叉树
平衡二叉树,我们也称【二叉平衡搜索树/AVL】,树中任何节点的两个子树的高度最大差别为1,巴拉巴拉。。。(https://baike.baidu.com/item/AVL树/10986648?fr=aladdin)
但是有个注意的点: 平衡二叉树的前提是 二叉排序树(https://baike.baidu.com/item/二叉搜索树/7077855?fr=aladdin)
这篇博客主要总结平衡二叉树,所以,二叉排序树知识不会提及,但是会用到。
如果想要看 排序二叉树调整为 平衡二叉树 旋转相关内容的,调整至 第5节。
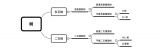
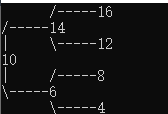
平衡二叉树
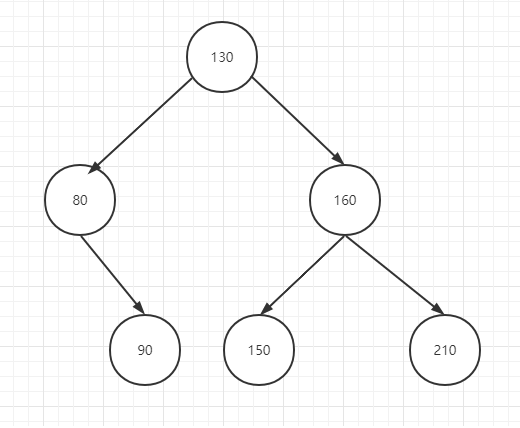
非平衡二叉树
最小不平衡子树节点为 130
左子树深度为 1,右子树深度为3 ,其差值大于1,所以不平衡
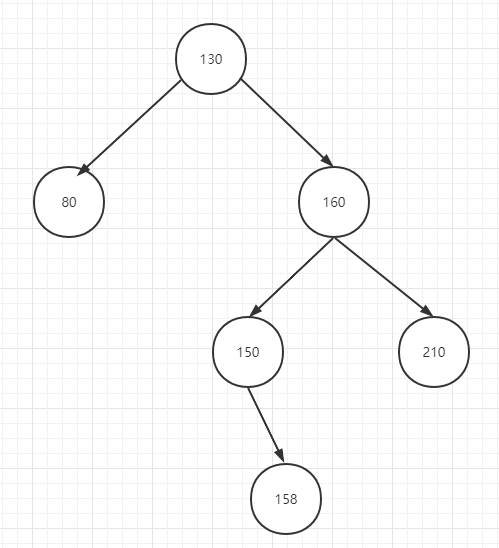
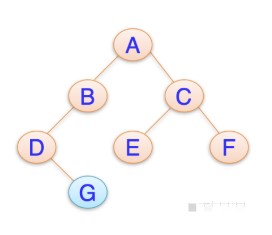
2. 如何判断二叉树最小不平衡子树
最小不平衡子树为 130 这颗子树(黄色标注)
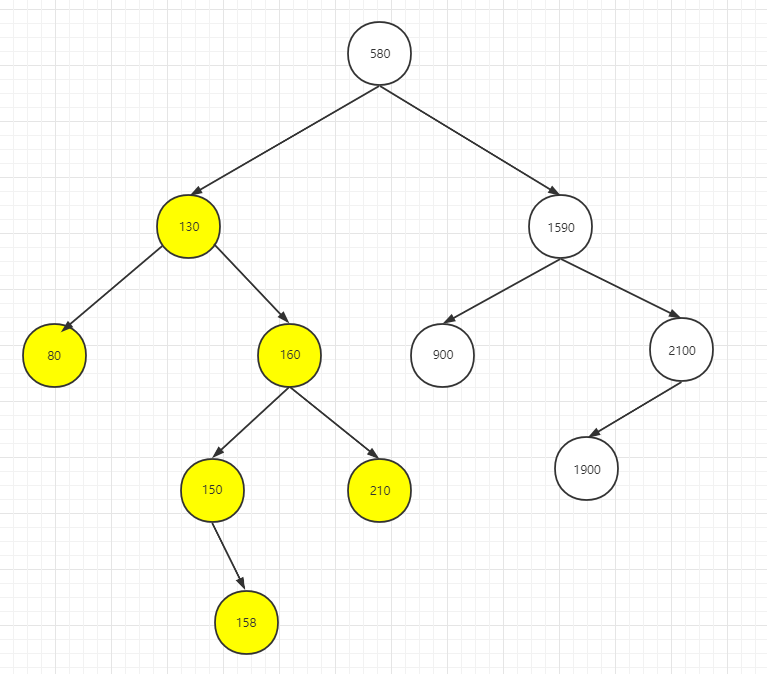
判定最小不平衡子树的关键就在于,判断这棵树的左子树 和 右字数 深度之差是否大于1,若大于1 ,则证明该树不平衡
检查二叉树是否平衡函数代码实现
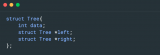
typedef struct {
int data; // 数据节点
struct TreeNode *left; // 指向左子树
struct TreeNode *right; // 指向右子树
} TreeNode , *PTreeNode;
// 记录平衡二叉树
bool BalanceTrue = false;
// 最小不平衡子树地址
TreeNode *rjt = NULL;
// 检查二叉树是否平衡,若不平衡 BalanceTrue 为 true
int checkTreeBalance(TreeNode *root) {
if (NULL == root) { return 0; }
int x = checkTreeBalance(root->left);
int y = checkTreeBalance(root->right);
// 若检测到最小不平衡二叉树后,不进行后面的检查
if (BalanceTrue) return 0;
int xx = abs(x-y);
if (xx > 1) {
// 左子树 和 右子树 相差大于1 , 二叉树不平衡
BalanceTrue = true;
rjt = root;
}
return (x>y?x+1:y+1);
}
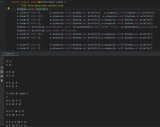
程序执行结果
# gcc -w -g -std=c11 BalanceTree.c
#
# ./a.out
当前二叉树遍历
前序遍历: 580 130 80 160 150 158 210 1590 900 2100 1900
中序遍历: 80 130 150 158 160 210 580 900 1590 1900 2100
二叉树不平衡,不平衡子树根节点为: 130
#
3. 二叉树不平衡情况
在一颗平衡二叉树的前提下,插入和删除一个节点,都有可能会引起二叉树不平衡,不平衡的情况主要有以下四种
左左更高
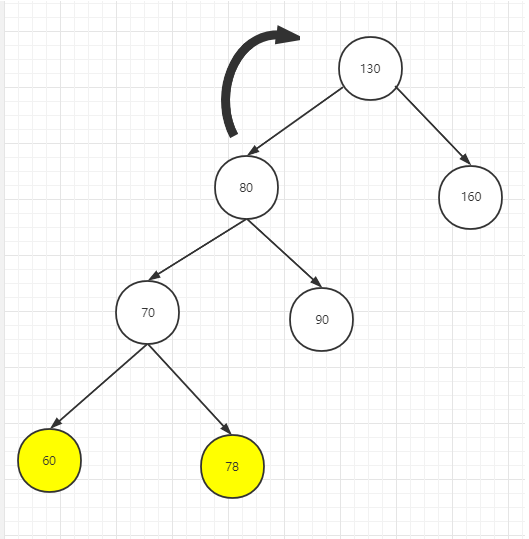
左右更高
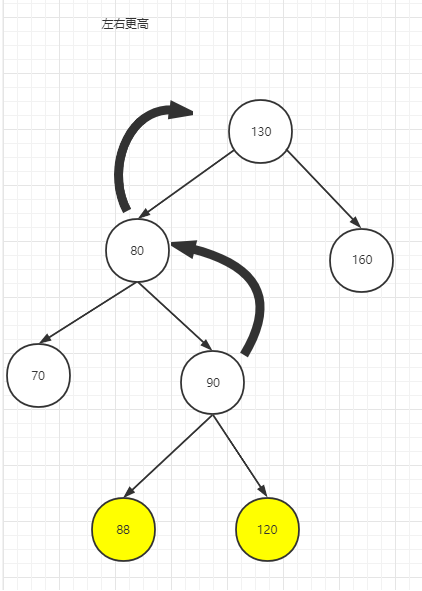
右左更高
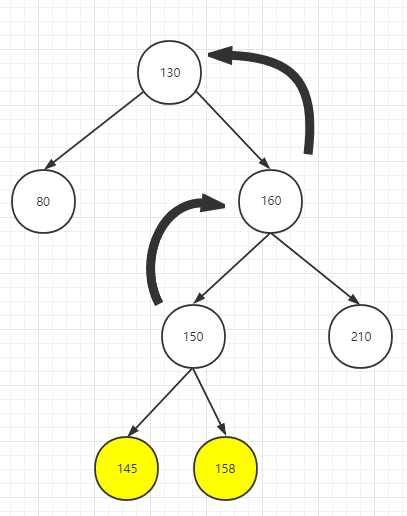
右右更高
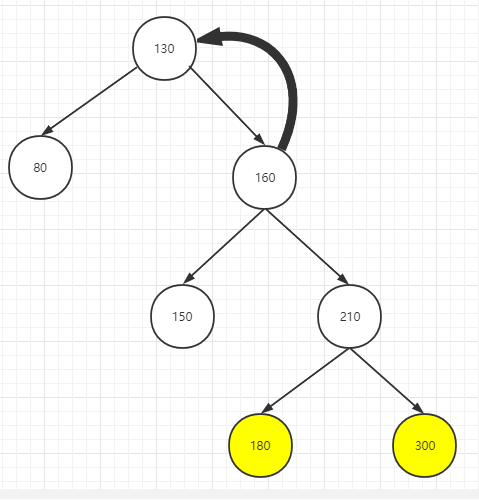
4. 判断不平衡二叉树哪边高
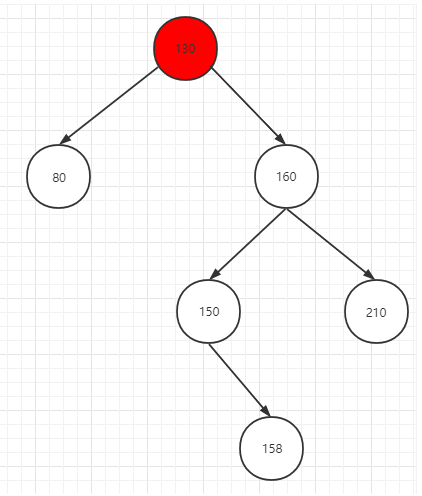
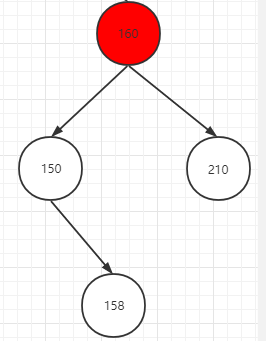
如上图红色所示,可以先根据最小不平衡二叉树左子树或者右子树高,上图所示,为右子树高,则将最小不平衡二叉树的右子树作为树根节点,继续判断子树的左子树或者右子树高。
比如上图的结果是右左较高,若进行调整的话,为先让不平衡子树右节点的树先向右旋转,然后再向左旋转。
判断不平衡二叉树哪边高代码实现
typedef struct {
int data; // 数据节点
struct TreeNode *left; // 指向左子树
struct TreeNode *right; // 指向右子树
} TreeNode , *PTreeNode;
// 记录平衡二叉树
bool BalanceTrue = false;
// 最小不平衡子树地址
TreeNode *rjt = NULL;
// 返回二叉树树高
int treeHeight(TreeNode *root) {
if (NULL == root) return 0;
int ll = treeHeight(root->left);
int rr = treeHeight(root->right);
return (ll>rr?ll+1:rr+1);
}
int main() {
/* 构建二叉树
判断平衡,获取最小不平衡子树, 将数据存入 rjt 中
输出二叉树 前序/中序
*/
if (BalanceTrue) {
printf("二叉树不平衡,不平衡子树根节点为: %d
",rjt->data);
} else {
return 0;
};
int ll = treeHeight(rjt->left);
int rr = treeHeight(rjt->right);
if (1 < ll - rr) {
printf("左子树高
");
TreeNode *rjt_ll = rjt->left;
int child_ll = treeHeight(rjt_ll->left);
int child_rr = treeHeight(rjt_ll->right);
if (child_ll > child_rr) {
printf("左子树更高
");
} else if (child_rr > child_ll) {
printf("右字数更高");
}
} else if (1 < rr - ll) {
printf("右子数高
");
TreeNode *rjt_rr = rjt->right;
int child_ll = treeHeight(rjt_rr->left);
int child_rr = treeHeight(rjt_rr->right);
if (child_ll > child_rr) {
printf("左子树更高
");
} else if (child_rr > child_ll) {
printf("右字数更高");
}
}
return 0;
}
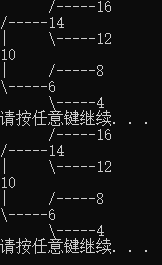
输出
# gcc BalanceTree.c -w -g -std=c11
#
# ./a.out
当前二叉树遍历
前序遍历:130 80 160 150 158 210
中序遍历:80 130 150 158 160 210
二叉树不平衡,不平衡子树根节点为: 130
右子数高
左子树更高
#
5. 如何调整平衡二叉树
所谓的旋转,其实是修改指针指向的值,仅此而已。
二叉树不平衡有四种情况
左左更高
原始二叉树,若要调整为平衡二叉树,需要整棵树向右旋转
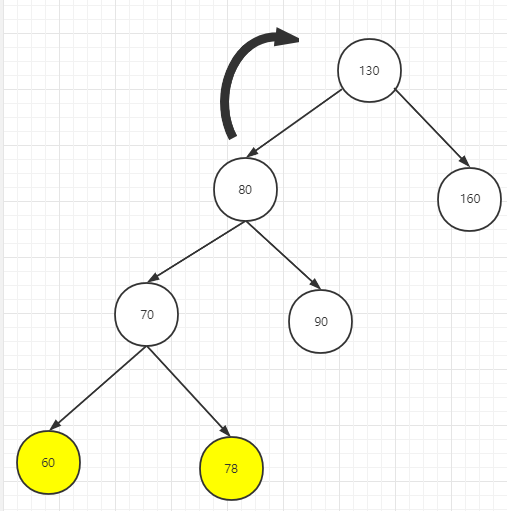
调整1:整棵树向右旋转
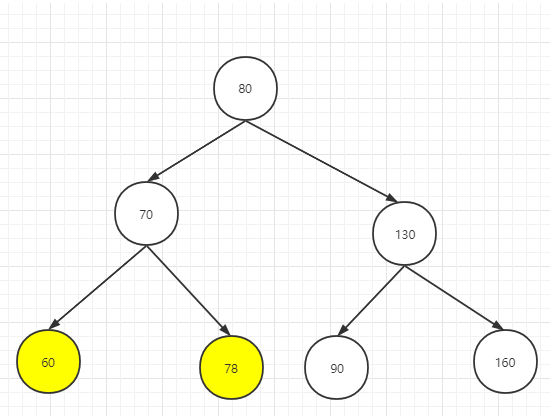
左右更高
原始二叉树,若要调整为平衡二叉树,需要先让不平衡子树左节点先向左旋转,然后再向右旋转
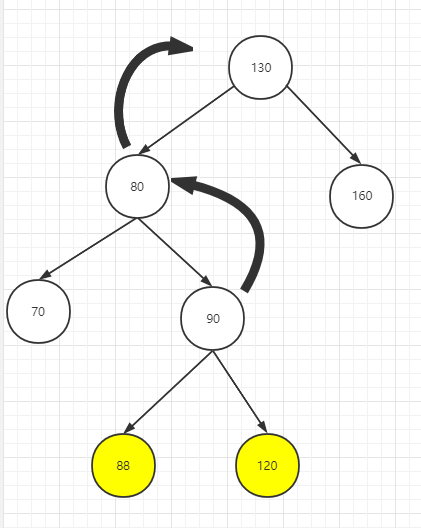
调整1: 先让不平衡子树左节点的树先向左旋转
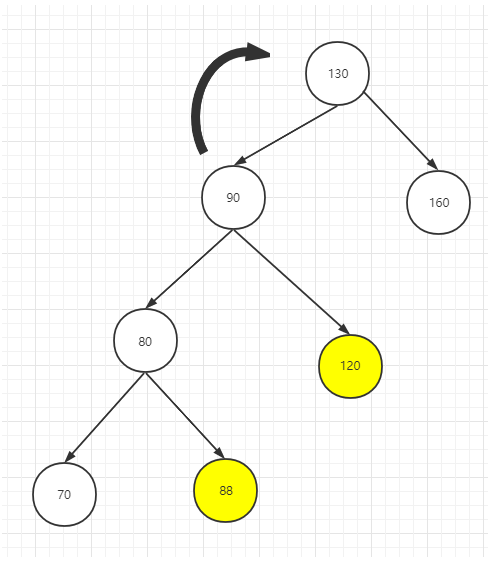
调整2:整棵树向右
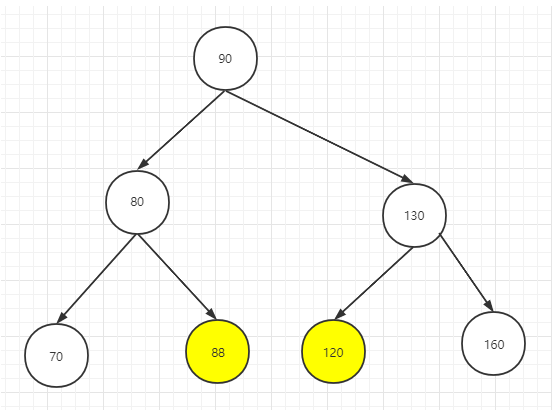
右左更高
原始二叉树,若要调整为平衡二叉树,需要先让不平衡子树右节点的树先向右旋转,然后再向左旋转
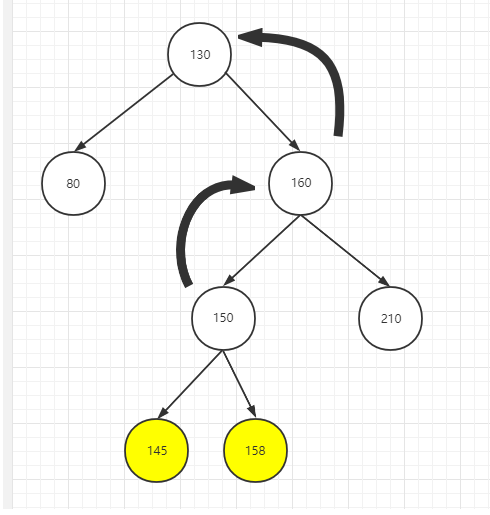
调整1: 先让不平衡子树右节点的树先向右旋转
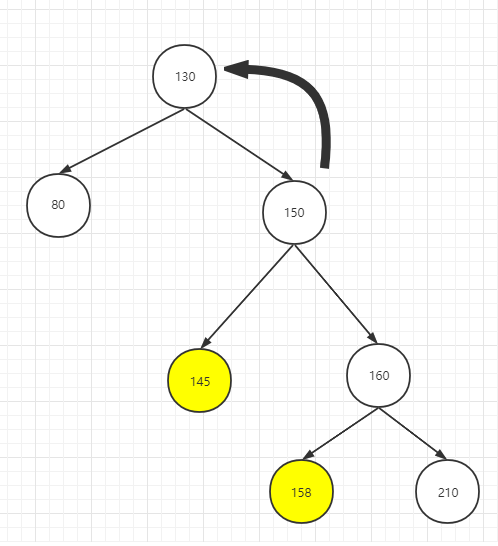
调整2:整棵树向左
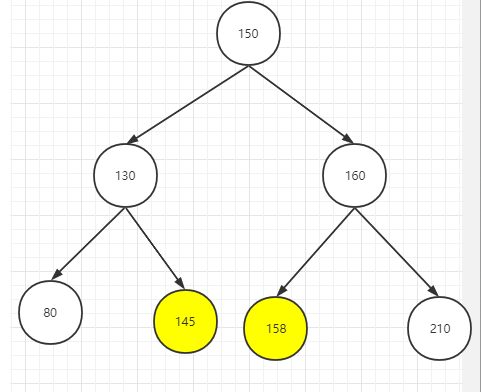
右右更高
原始二叉树,若要调整为平衡二叉树,需要整棵树向左旋转
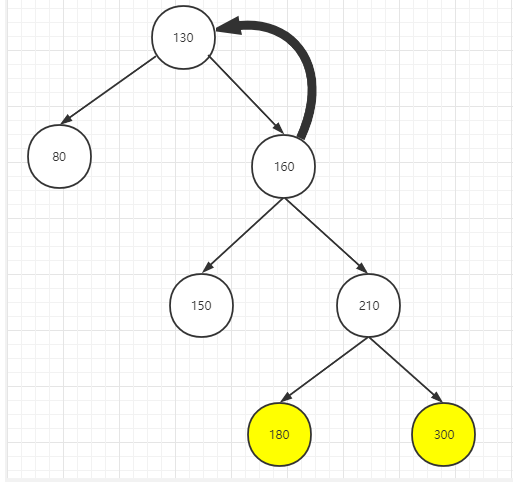
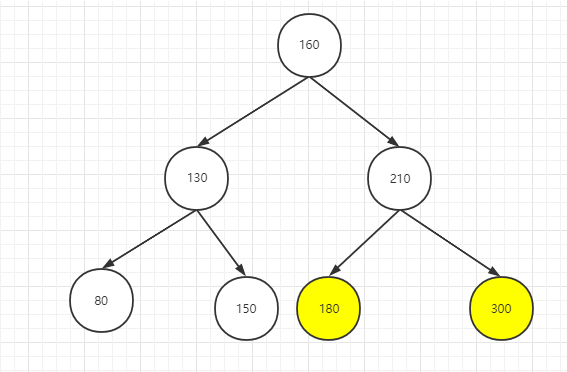
调整1:整棵树向左旋转
全部代码
# include
程序执行结果
# gcc BalanceTree.c -w -g -std=c11
#
# ./a.out
平衡二叉树插入测试
插入数据: 65
插入数据: 60
插入数据: 70
插入数据: 55
插入数据: 40
二叉树不平衡,最小不平衡子树数据结点: 60
左左旋转,非根节点
二叉树调整平衡后数据结点:
前序遍历:65 55 40 60 70
中序遍历:40 55 60 65 70
插入数据: 63
二叉树不平衡,最小不平衡子树数据结点: 65
左右旋转,是根节点
二叉树调整平衡后数据结点:
前序遍历:60 55 40 65 63 70
中序遍历:40 55 60 63 65 70
插入数据: 69
插入数据: 66
二叉树不平衡,最小不平衡子树数据结点: 70
左左旋转,非根节点
二叉树调整平衡后数据结点:
前序遍历:60 55 40 65 63 69 66 70
中序遍历:40 55 60 63 65 66 69 70
插入数据: 68
二叉树不平衡,最小不平衡子树数据结点: 65
右左旋转,非根节点
二叉树调整平衡后数据结点:
前序遍历:60 55 40 66 65 63 69 68 70
中序遍历:40 55 60 63 65 66 68 69 70
插入数据: 77
二叉树不平衡,最小不平衡子树数据结点: 60
右右旋转,是根节点
二叉树调整平衡后数据结点:
前序遍历:66 60 55 40 65 63 69 68 70 77
中序遍历:40 55 60 63 65 66 68 69 70 77
当前二叉树遍历
前序遍历:66 60 55 40 65 63 69 68 70 77
中序遍历:40 55 60 63 65 66 68 69 70 77
平衡二叉树删除测试
删除节点: 70
删除节点: 55
删除节点: 40
二叉树不平衡,最小不平衡子树数据结点: 60
右左旋转,非根节点
二叉树调整平衡后数据结点:
前序遍历:66 63 60 65 69 68 77
中序遍历:60 63 65 66 68 69 77
当前二叉树遍历
前序遍历:66 63 60 65 69 68 77
中序遍历:60 63 65 66 68 69 77
#
审核编辑:汤梓红
-
C语言
+关注
关注
180文章
7614浏览量
137654 -
二叉树
+关注
关注
0文章
74浏览量
12373
原文标题:平衡二叉树 C语言代码实现
文章出处:【微信号:技术让梦想更伟大,微信公众号:技术让梦想更伟大】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
基于二叉树的时序电路测试序列设计
二叉树层次遍历算法的验证
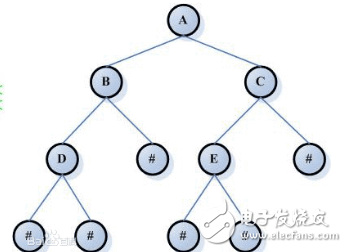
二叉树操作的相关知识和代码详解
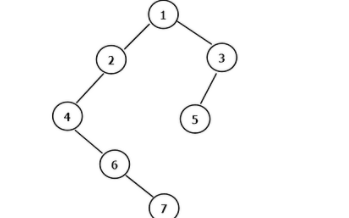




 使用C语言代码实现平衡二叉树
使用C语言代码实现平衡二叉树










评论