与电容器和电阻器一样,电感器也是无源元件。简单地说,电感器是导电材料的绞合线或线圈。电感是电导体或电路的特性,它反对电流的变化。
简单来说,具有电感特性的电导体或电路元件称为电感器。当线圈或绞合线(电感器)中的电流发生变化时,它会通过在自身和附近的导电材料中产生或感应电动势 (EMF) 来对抗这种变化。
电感器以磁场的形式存储能量。由于磁场与电流有关,电感与载流材料有关。塑料、木材和玻璃等介电材料的电感最小。但铁磁性物质(铁、铝镍钴、三氧化二铬)会有很高的电感。
线圈中的电感主要两种类型,它们是自感和互感。那么,自感和互感的有什么区别,其计算公式又是什么?下面分别来介绍下。
自感
自感是载流导体的特性,当电流发生变化时,其中会感应出EMF。
当交流变化的电流流过电感线圈时,线圈中的磁通量也会发生变化,从而产生感应电动势。这个过程称为“自感”,线圈实现的电感称为“自感”。
自感的概念可以通过假设载流电路元件或N匝电感线圈来理解,当电流流过线圈时,会在线圈内外产生磁场。由于该磁场而引入了磁通量。那么,线圈的自感就是每单位电流的磁链。当电感线圈与由电场引起的磁力线相交时,线圈本身就会产生自电动势。
换句话说,自感是指线圈抵抗电流变化的能力。它以亨利为单位。线圈的磁性或磁性会影响线圈的自感。这就是为什么使用铁磁材料通过增加线圈中的磁通量来增加线圈的电感的原因。
求线圈自感的表达式为:L = N Φ /I
其中N代表线圈的匝数,Φ是磁通量,I是由于产生的电动势而产生的电流,L表示以亨利为单位的电感值。
自感电动势和自感系数
我们知道流过电感的电流用I表示,Φ是磁通量,它们都彼此成正比,所以它可以表示为 I ∝ Φ。
电感器的匝数也与线圈中的电流成正比,所以可以推导出电流与其中感应的电动势之间的关系为:(dΦ)/dt = L (di)/dt
电感值取决于线圈的几何形状或形状,该值称为“自感系数”。
e = – (dΦ)/dt
e = – L (di )/dt
我们可以根据需要设计电感线圈,使用高磁导率或低磁导率材料,并使用不同匝数的线圈。电感器铁芯内部产生的磁通量为:Φ = B x A,这里B是磁通密度,A是线圈占据的面积。
示例1:长螺线管中的自感
如果考虑一个长的中空螺线管,其横截面积为A,长度为l,匝数为n,则由于电流I的流动,其磁场为:B = μ0 H = μ0(NI )/l,螺线管中的总通量为 N Φ = LI。
将其代入上述等式,则有:L = N Φ /I ,L = (μ0 N 2 A )/ l
其中L是亨利的自感,μ0是空气或中空空间的渗透率,N代表线圈即电感的匝数,A是螺线管的内横截面积,l是线圈的长度且以米为单位。
以上就是长的空心螺线管的自感。μ表示填充螺线管的材料的绝对磁导率。在这种情况下,我们计算了空心螺线管的自感,因此使用μ0。为了获得高磁导率或产生高磁通量,可以用软铁等铁磁物质填充螺线管。
示例2:圆形线圈的自感
考虑一个横截面积为A=π r2的圆形线圈,其中匝数为N。则磁通量为:B = μ0 (NI )/2r,圆形导体中的总通量为N Φ = LI。
将其代入上述等式,则有:
L = N Φ /I ,L = (μ_0 N 2 A )/2r
众所周知,圆的面积是A = π r 2,所以圆形电感的自感也可以表示为:L = (μ0 N 2 π r )/2
影响自感的因素
观察上面的电感方程可以清楚的知道,共有4个因素会影响线圈的自感,它们是:
线圈匝数(N)
电感线圈面积 (A)
线圈长度 (l)
线圈材料
1、线圈匝数
线圈的电感取决于线圈的匝数,线圈中的匝数或捻数与电感成正比,即:N∝L。
所以,匝数越高意味着电感值越大,而减少匝数意味着降低电感值。
2、横截面面积
线圈的电感会随着电感器横截面积的增加而增加,即:L∝N。如果线圈的面积大,它会产生更多的磁通量线,这导致形成更多的磁通量,因此电感会很高。
3、线圈长度
长线圈感应的磁通量小于短线圈感应的磁通量。随着感应磁通量减少,线圈的电感也减少。所以线圈的感应与线圈的电感成反比,即:L∝ 1/l。
4、线圈材料
包裹线圈的材料的磁导率将对感应电动势和电感产生影响。具有高磁导率的材料可以产生低电感,即:L∝μ0。
我们知道 μ = μ0 μr,所以 L∝ 1 / μr
互感
由于其耦合或相邻线圈的电流变化而在线圈中感应电动势的现象称为“互感”,这里两个线圈受到相同磁场的影响。由互感产生的电动势可以用法拉第定律来解释,而电动势的方向可以用楞次定律来描述。
电动势的方向总是与磁场的变化相反。第二个线圈中感应的电动势是由于第一个线圈的电流变化引起的。第二个线圈中感应的电动势可以表示为:
EMF2 = – N2 A ΔB/Δt = -M (ΔI1)/Δt
其中M是互感,它是第二个线圈中产生的电动势与第一个线圈中的电流变化之间的比例。
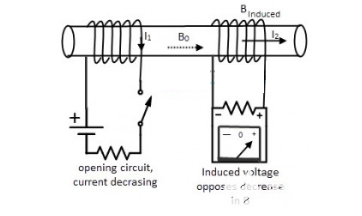
要了解互感的概念,可以观看上图。在连接的两个电感器缠绕在单个导体上,假设它们为回路1和回路2。如果回路1中的电流发生变化,则感应出磁通量。当回路2截断磁通量时,没有任何电流直接流入第二个线圈,将产生一些感应电动势,这种现象称为“互感”。
互感电动势和互感系数
每当将2个线圈保持在电流变化场中时,都会因为电流而感应出电动势。随着回路中的电流变化,磁通量也会变化。
在这种情况下,互感是一个矢量,因为它可能由于第一线圈中的电流而在第二线圈中感应,或者可能由于第二线圈产生的磁通量(B)而在第一线圈中感应。
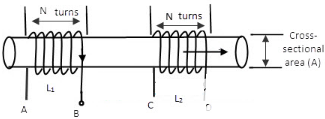
当电感器1中流动的电流发生变化时,会在其周围产生磁通量(根据楞次定律和法拉第定律)。然后,由于第一个线圈中的电流,第二个线圈中的相互感应电动势将被给出为:
M12 = (N2 Φ12)/I1
其中M12是线圈2中的互感,N是循环中的匝数,Φ12是线圈2中产生的磁通量,I1是回路1中的电流。
同样,当我们改变电感器1中的电流时,会在其周围产生磁通量。那么由于第2线圈中的电流而在第1线圈中产生的互感电动势将给出为:
M21 = (N2 Φ21)/I2
其中M21是线圈1中的互感,N是循环中的匝数,Φ21是线圈1中产生的磁通量,I2是回路2中的电流。
需要记住的重要一点是,M21 = M12 = M,与两个线圈的相对位置、大小和匝数无关。这称为“互感系数”。
每个线圈的自感公式为:
L1 = (μ 0 μr N1 2 A)/l 和 L2 = (μ 0 μr N2 2 A)/l
从上面的等式,可以写出 M2 = L1 L2。这是每个线圈的自感与互感之间的关系。当然,它也可以写成M = √(L1 L2 ) Henry。
上式表示没有磁通泄漏的理想条件,但实际上,由于线圈的位置和几何形状,总会存在一些磁漏。
磁耦合系数或耦合系数
两个线圈之间的电感耦合量用“耦合系数”表示。耦合系数的值将小于1并始终大于0,即介于0和1之间,用“k”表示。
耦合系数的推导
考虑两个分别具有N1和N2匝长度为L1和L2的电感线圈。线圈1和2中的电流为I1和I2。假设由于电流I1在第二线圈中产生的磁通量为Φ21。则互感为M = N1 Φ21/ I1
Φ21可以描述为磁通Φ1与第二线圈相连的部分,即Φ21 = k1 Φ1
… M = N1 ( k1 Φ1) / i1 。. . . . . . . . . (1)
类似地,由于电流I2在第一线圈中产生的通量为Φ12,则互感为M = N2 Φ12/ I2
Φ21可以描述为磁通Φ1 与第二线圈相连的部分,即Φ12 = k2 Φ2
… M = N2 ( k2 Φ2) / i2 。. . . . . . . . . (2)
将等式 (1) 和 (2) 相乘,得到:
M = k1 k2 [N(1 Φ1 )/I_1 ].[N(2 Φ2 )/I2 ]
然后通过已知条件,可以推出耦合系数K= M/((√(L1 L2 )) )。
注意:
K值永远不会是负数或永远不会是小数值。
铁芯或铁氧体磁芯耦合电路的耦合系数为k=0.99
空芯耦合电路的耦合系数k=0.4~0.7
总结
电感器中的感应可以用楞次定律和法拉第定律来解释。楞次定律指出,“在电流方向上产生的感应电动势与产生该电动势的磁通量相反”。线圈中的电感有两种类型,它们是自感和互感。
线圈的自感是放置在电流变化电路中时在土壤中感应出的电动势,这种自感现象称为“自感”。用L表示,L = N Φ /I。
由于其耦合线圈的电流变化而在线圈中感应出电动势的现象称为“互感”,用M表示,M = √(L1 L2 )
两个线圈之间的电感耦合量用“耦合系数”表示。耦合系数的值将小于1并始终大于0,用“k”表示,K = M/((√(L1 L2 )) )。
-
电容器
+关注
关注
64文章
6227浏览量
99755 -
电阻器
+关注
关注
21文章
3784浏览量
62171 -
电感器
+关注
关注
20文章
2333浏览量
70561
发布评论请先 登录
相关推荐




 自感和互感的区别及其计算公式
自感和互感的区别及其计算公式












评论