在昨天的文章中我们介绍了品质因数Q0的相关概念,这篇文章主要翻译自一篇英文文档,上面的很多概念都是泛泛而谈。 关于Q0和3dB带宽的关系,有同学留言求证,今天我们唠叨唠叨这个。 单纯看符号的字面意思,我们很难将品质因数Q0和带宽BW联系起来,尤其是还有中心频率F0. 今天我们一起来解一下这个问题。Q0到底是怎么和频率/带宽扯上关系的呢? 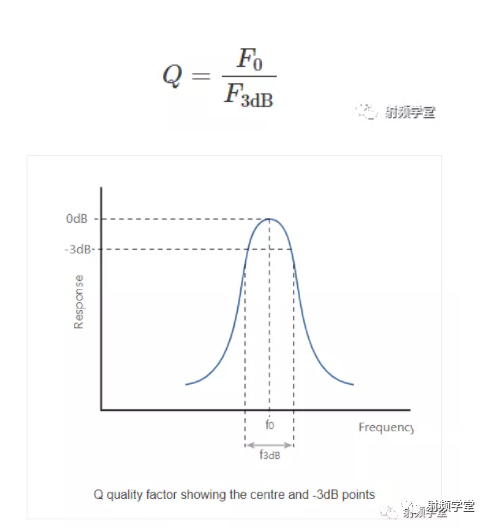 这个还要从Q0的最初定义来解答。Q0是描述一个谐振回路品质好坏的一个参量,其定义为一个周期内储能和平均耗能的比值。这个谐振回路既可以是RLC串联谐振回路,也可以是RLC并联谐振回路。
这个还要从Q0的最初定义来解答。Q0是描述一个谐振回路品质好坏的一个参量,其定义为一个周期内储能和平均耗能的比值。这个谐振回路既可以是RLC串联谐振回路,也可以是RLC并联谐振回路。 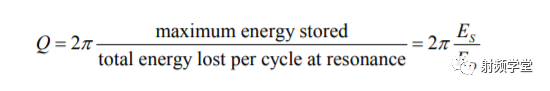 我们以一个RLC串联谐振回路为例。
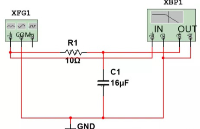
我们以一个RLC串联谐振回路为例。 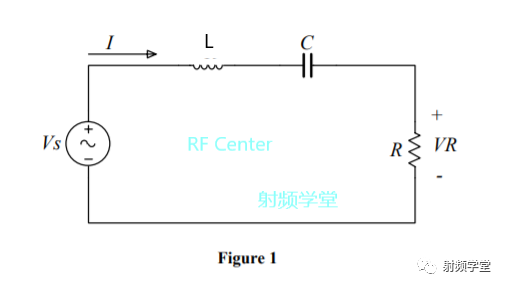 这个电路在电阻R上的传输函数H(w)的幅度值如下:
这个电路在电阻R上的传输函数H(w)的幅度值如下: 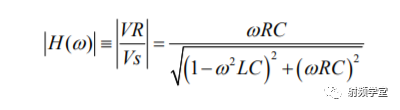 在谐振频率点w0处,传输函数H(w)的幅度最大等于1,
在谐振频率点w0处,传输函数H(w)的幅度最大等于1, 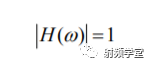 H(ω)的幅度值随着电阻R的不同,响应曲线如下图所示:
H(ω)的幅度值随着电阻R的不同,响应曲线如下图所示: 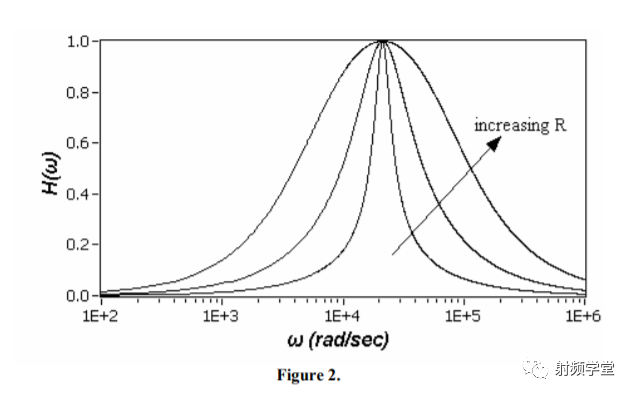
undefined
上图那个幅度值最大的点对应的频率就是RLC串联谐振电路的谐振频率。观察上图,确实发现3dB带宽和R有某种特殊的关系,R越大,3dB带宽越大。 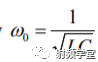 在RLC串联谐振回路中,单位周期内消耗的功率就是电阻R消耗的功率P(w)。
在RLC串联谐振回路中,单位周期内消耗的功率就是电阻R消耗的功率P(w)。 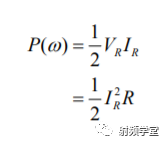 P(w)是一个关于频率的函数,当在谐振点处,电阻消耗的功率P(w)最大:
P(w)是一个关于频率的函数,当在谐振点处,电阻消耗的功率P(w)最大: 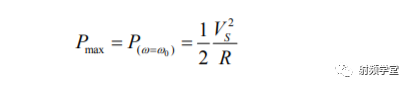 我们做出传输函数H(w)的功率传输曲线,如下图。看看3dB带宽是怎么来的?
我们做出传输函数H(w)的功率传输曲线,如下图。看看3dB带宽是怎么来的? 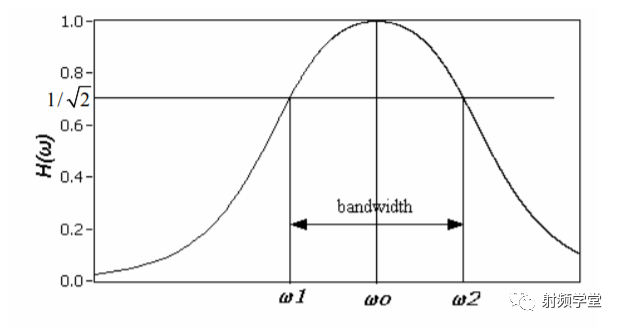 3dB带宽,也就是当功率下降一半的时候的带宽。这个3dB来自于10log(1/2)。当功率下降一半,也就是电压下降1/根号(2)时。这时候有:
3dB带宽,也就是当功率下降一半的时候的带宽。这个3dB来自于10log(1/2)。当功率下降一半,也就是电压下降1/根号(2)时。这时候有: 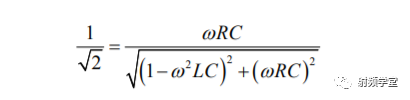
求解上式就可以得到w的两个根,分别是w1和w2
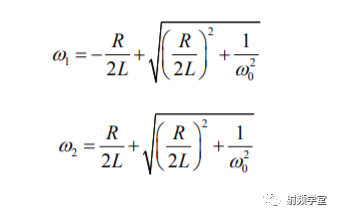
这时候,3dB带宽就可以得到了:
BW 3dB=w2-w1=R/L
undefined
记住了,3dB带宽就和电阻R和电感L联系起来了。这个就为品质因数Q0和带宽的关系埋下了伏笔。
我们接着看RLC串联谐振回路的Q0的计算。在RLC谐振回路的总储能等于电感和电容储能的和:
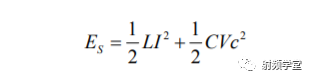
在给定电流和电压情况下,总储能Es可以表示为:
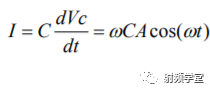
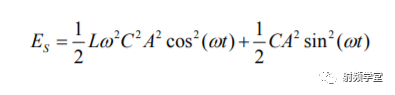
在谐振点w0处,
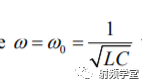
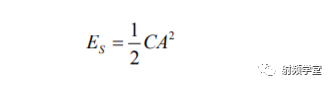
而单位周期内的平均耗能Ed就可以表示为:
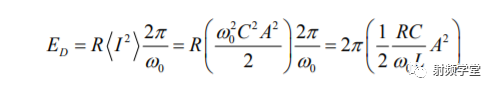
那这个品质因数Q0的公式就可以表示为:
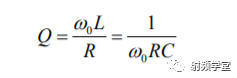
我们只取前面Q0和电感的关系:
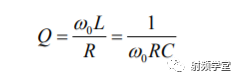
把3dB带宽的公式带入就可以得到:
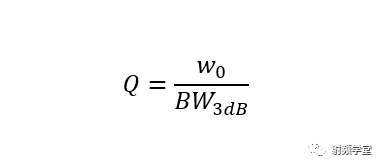
当然角频率w和频率f的关系带入就得到了这个关系,这个Q值和频率的关系,对于实际电路的测试有很大的用处,大大简化了Q0的测试。
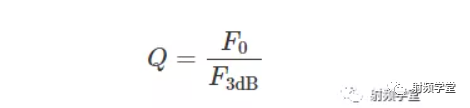
到这里,大家是不是就清楚了。
同理用RLC并联谐振回路也能得到同样的结果。
表格给出了LC谐振回路最基本的特性公式。不用记住,有个印象就行。

-
电阻
+关注
关注
86文章
5575浏览量
173231 -
带宽
+关注
关注
3文章
965浏览量
41222 -
函数
+关注
关注
3文章
4352浏览量
63250
发布评论请先 登录
相关推荐
ths3091带宽只能到达7Mhz就已经达到3DB衰减,为什么?
3dB 90°电桥
3dB电桥的用途
放大器手册中-3db带宽定义是怎样的?
AD4084-2增益带宽积GBP和-3dB的区别是什么?
3dB电桥原理
什么是-3dB?ATA-1000系列宽带放大器最大带宽是多少?
-3dB、0.707、截止频率三者关系





 Q0和3dB带宽的关系
Q0和3dB带宽的关系











评论