区块链交易隐私如何保证？华为零知识证明技术实战解析

什么是零知识证明？

证明者在不泄露任何有效知识的情况下，验证者可以验证某个论断是正确的。图1给出一个有趣的例子，Alice把自己的签名的信封放到一个保险箱中，Bob说他知道这个保险箱的密码，Alice让Bob证明给她看。Bob打开保险箱，把信封拿出来给Alice。Alice验证信封上的签名，确认了Bob确实知道这个密码。这个例子就是Bob没有告诉Alice密码却证明自己知道密码的的过程很好的解释了零知识证明的概念。基于非对称加密和数字签名的证书认证过程，其实也是一个零知识证明的过程，验证者并不需要知晓CA证书，就可以验证对方是由CA签发的下一级证书。零知识证明技术不管应用于金融还是其他领域，都可以对隐私保护，性能提升，或者安全性等场景带来很多帮助。下面，主要从隐私维度来分享华为零知识证明相关技术。

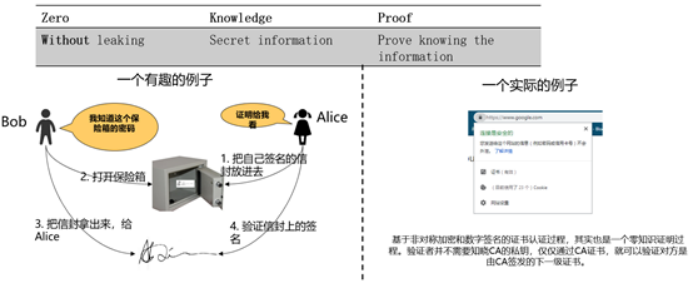
图1 零知识证明

零知识证明应用于同态加密保护交易隐私，使能金融业务

目前金融转账交易场景中对于隐私保护已经越来越重视，隐私也成为区块链急需解决的一个重要问题。那基于如下问题, A向B转账10元，需要区块链节点记账，但是不想让区块链节点知道交易金额以及最新余额，也是金融场景中一个非常常见的问题。

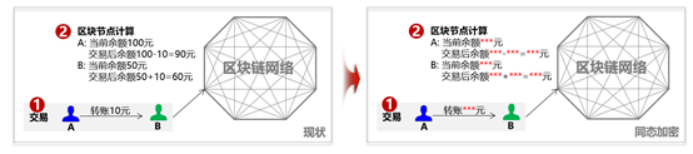
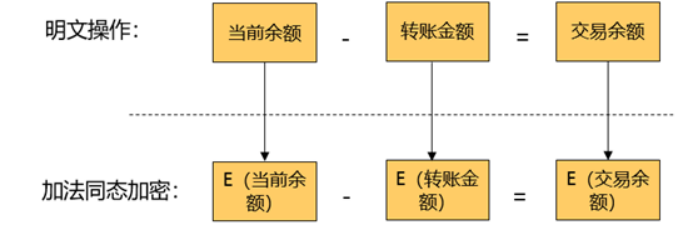
图2同态加密

基于这种场景如何解决区块链技术应用于金融的隐私和可用性？华为目前引入同态加密(解决隐私问题)。同态加密（英語：Homomorphic encryption）是一种加密形式，它允许人们对密文进行特定形式的代数运算得到仍然是加密的结果，将其解密所得到的结果与对明文进行同样的运算结果一样。换言之，这项技术令人们可以在加密的数据中进行诸如检索、比较等操作，得出正确的结果，而在整个处理过程中无需对数据进行解密。在此基础上创新式提出了 同态加密范围证明 (一种针对数字的零知识证明技术，在不泄露具体数字值的情况下，获得数字的范围，从而验证数字所代表的交易的有效性)。

基于集成到区块链系统中的同态加密库以及修改同态加密库实现的零知识证明能力实现了隐私转账的能力，一个密文和另一个密文相加或相乘实现转账中的密文交易，零知识证明在整个的计算过程中不暴露任一方的信息证明对方可以完成转账这一流程，在不泄露具体数字的情况下得到数字的范围。从而验证数字所代表交易的有效性。

使用同态加密库的app端sample代码示例

下面我们看一下零知识证明在代码中是如何应用的，Demo代码使用地址：https://support.huaweicloud.com/devg-bcs/bcs_devg_0020.html。下面讲解的代码都可以在上面的地址中下载全量代码查看。

func** transaction() error **{

** addrA := **calcAddr( userdata . PubKey )

** setup := **& sdk_client . BaseSetupImpl {

** ** ConfigFile :** conf**,

** ** ChannelID :** channelid**,

** ** OrgID :** orgid**,

** ** ConnectEventHub :** **false,

** ** ChainCodeID :** idchaincode**,

** **}

** if err := setup**.Initialize();** err != nil **{

** ** fmt .Println("fail to init sdk: ",** err**.Error())

** ** return** errors**.New("fail to init sdk: "** + err**.Error())

** **}

** setup**.ChainCodeID = txchaincode

** transRec := sdk_client**. TransRecord {}

** resps, err := sdk_client**.Query( setup ,** "QueryBalance", **[][]byte{[]byte( addrA )})

** if err != nil **{

** ** fmt .Println("Fail to query balance of sender: ",** err**.Error())

** ** return** err**

** **}

** err = json**.Unmarshal( resps [0]. ProposalResponse .GetResponse(). Payload ,** **& transRec )

** if err != nil **{

** ** fmt .Println("fail to unmarshal balance result: ",** err**.Error())

** ** return** err**

** **}

** var pubKeyB **string

** **setup.ChainCodeID = idchaincode

** resps, err = sdk_client**.Query( setup ,** "QueryPubkey", **[][]byte{[]byte( addrB )})

** if err != nil **{

** ** fmt .Println("Fail to query pubkey of receiver: ",** err**.Error())

** ** return** errors**.New("Fail to query pubkey of receiver: "** + err**.Error())

** **}

** pubKeyB = **string( resps [0]. ProposalResponse .GetResponse(). Payload )

** **fmt.Println("Get B's ID successfully")

** cipherBalanceAKeyA := transRec**.Balance

** txInfoSer, err := pswapi_sdk**.PrepareTxInfo( cipherBalanceAKeyA ,** tx**,** userdata**. PubKey ,** pubKeyB**,** userdata**. PriKey ,** propwd**)

** if err != nil **{

** ** fmt .Println("fail to prepare tx info: ",** err**.Error())

** ** return** errors**.New("fail to prepare tx info: "** + err**.Error())

** **}

** **setup.ChainCodeID = txchaincode

** _, err = sdk_client**.Invoke( setup ,** "Transfer", [][]byte{[]byte( addrA ), []byte( addrB ), **[]byte( txInfoSer )})

** if err != nil **{

** ** fmt .Println("Invoke Transfer error for user: ",** addrA**,** err**.Error())

** ** return** errors**.New("Invoke Transfer error for user: "** + addrA + err**.Error())

** **}

** return **nil}

图3同态加密业务代码

图3是同态加密的实现业务代码，首先写一个transaction的方法，返回值是error。第一步需要进行初始化获取sdk_client对象也就是setup变量。然后通过sdk_client.Querry方法基于key“QueryBalance“查询账户A的加密余额,同样的方法基于key "QueryPubkey"拿到b的公钥。第二步PrepareTxInfo方法构建A向B的转账信息，最后一步通过invoke调用完成A到B的转账的过程。

func** ( t *** TransChaincodeDemo ) transfer( stub shim . ChaincodeStubInterface , args [] string ) pb** .**Response **{

** AddrA := args**[0]

** AddrB := args**[1]

** txInfo := args**[2]

** if strings**.Compare( AddrA ,** AddrB**)** == 0 **{

** logger**.Error("A' addr is the same B'Addr")

** return shim**.Error("A' addr is the same B'Addr")

** **}

** transRecA**,** err := stub**.GetState( AddrA )

** if err != nil **{

** return shim**.Error("Failed to get state")

** **}

** if transRecA == nil **{

** return shim**.Error("Entity not found")

** **}

** var transRecAStruct = TransRecord**{}

** err = json**.Unmarshal( transRecA ,** **& transRecAStruct )

** if err != nil **{

** logger**.Error("fail to unmarshal user's trans record")

** return shim**.Error("fail to unmarshal user's trans record")

** **}

** transRecB**,** err := stub**.GetState( AddrB )

** if err != nil **{

** return shim**.Error("Failed to get state")

** **}

** if transRecA == nil **{

** return shim**.Error("Entity not found")

** **}

** var transRecBStruct = TransRecord**{}

** err = json**.Unmarshal( transRecB ,** **& transRecBStruct )

** if err != nil **{

** logger**.Error("fail to unmarshal user's trans record")

** return shim**.Error("fail to unmarshal user's trans record")

** **}

** cipherBalanceAKeyABlock := transRecAStruct**.Balance

** cipherBalanceBKeyBBlock := transRecBStruct**.Balance

** newCipherBalanceA**,** newCipherBalanceB**,** newCipherTxA**,** newCipherTxB**,** err := pswapi_cc**.ValidateTxInfo( txInfo ,** cipherBalanceAKeyABlock**,** cipherBalanceBKeyBBlock**)

** if err != nil **{

** logger**.Error("fail to validate trans information")

** return shim**.Error("fail to validate trans information")

** **}

** transRecAStruct**.Balance = newCipherBalanceA

** transRecAStruct**.TX** = newCipherTxA**

** transRecAStruct**.**TXType = **"P"

** AvalbytesUpdate**,** err := json**.Marshal( transRecAStruct )

** if err != nil **{

** logger**.Error("fail to marshal balance update info")

** return shim**.Error("Marshal Error")

** **}

** err = stub**.PutState( AddrA ,** AvalbytesUpdate**)

** if err != nil **{

** logger**.Error("fail to store state: ",** err**.Error())

** return shim**.Error( err .Error())

** **}

** transRecBStruct**.Balance = newCipherBalanceB

** transRecBStruct**.TX** = newCipherTxB**

** transRecBStruct**.**TXType = **"R"

** BvalbytesUpdate**,** err := json**.Marshal( transRecBStruct )

** if err != nil **{

** logger**.Error("fail to marshal balance update info")

** return shim**.Error("Marshal Error")

** **}

** err = stub**.PutState( AddrB ,** BvalbytesUpdate**)

** if err != nil **{

** return shim**.Error( err .Error())

** **}

** return shim**.Success([]byte("Success"))}

图4同态加密链代码

图4 是同态加密核心的transfer链代码，在这个方法中首先通过getstate获取A和B两个账户的当前余额，然后最重要的一步，是验证他的余额，在方法validatetxinfo中会基于范围/等式证明验证交易数据的合规性，基于同态加密算法计算交易后的账户余额，最后更新交易后A账户和B账户的余额。同态加密的这一步中，应用了零知识证明的相关的技术和能力来促进同态加密更加高效和安全。

基于zksnark的零知识证明技术

交互式证明和非交互式证明

图5交互式证明

零知识证明又分为交互式证明和非交互式证明，有两个有趣的例子很好的解释了这个概念。如上图5所示，男子向女子声称有CD处的钥匙，女子不相信说“你拿出来给我看啊”，男子想“你让我拿我就拿多没面子啊”，男子说”这样吧，按下面步骤玩个游戏”

1.女子站在A点

2.男子从B点走到C点或者D点

3.男子从B点消失后，女子从A点走到B点

4.女子喊话“从左边出来”，或者“从右边出来”

5.男子按照女子的要求从对应一侧走出

女子说“你肯定作弊，刚才我喊左边出来，你刚好就是从左边进去的”，

男子说：“你回到A点，我们再来一遍”

如果每次都成功，说明B确实有CD处的钥匙，该证明是需要A，B不停的交互。

非交互式零知识（NizK）证明方案由算法设置、证明和验证定义，具体来说，我们有params=Setup()，其中输入是安全参数，输出是ZKP算法系统的参数。证明语法由证明=证明（x,w）给出。该算法接收某些NP语言L的实例x和见证w作为输入，并输出零知识证明。验证算法接收证明作为输入，并输出位b，如果验证者接受证明，则该位等于1。通俗一点就比如说我有一个秘密，我不想告诉别人，但是我又得让别人相信。我是知道这个秘密的，类似于这种，但是我们为什么需要有这种非交互式呢？因为交互式证明的其实只对原始的验证者有效，其他的任何人都不能够信任这个证明。这种场景下呢，就会导致这个验证者可以和这个证明人串通，证明人可以伪造证明。验证者也可以用这种方式做一些伪造。因此，验证者必须保存一些数据，直到相关的证明被验证完毕。这样就会造成一些秘密参数泄露的这种风险。这种交互式证明也有它的用处，就比如说一个证明人只想让一个特定的验证者来去验证，但是这个证证明人和验证者必须保持在线，并且去对每一个验证者执行同样的计算。

什么是zk-snark？

zk-SNARK是Zero-knowledge succinct non-interactive arguments of knowledge的缩写，他的意思是：zero knowledge：零知识，即在证明的过程中不透露任何隐私数据：succinct：简洁的，主要是指验证过程不涉及大量数据传输以及验证算法简单；non-interactive：无交互。证明者与验证者之间不需要交互即可实现证明，交互的零知识证明要求每个验证者都要向证明者发送数据来完成证明，而无交互的零知识证明，证明者只需要计算一次产生一个proof，所有的验证者都可以验证这个proof。zk-SNARK是证明某个声明是真却不泄露关于该声明的隐私信息的一个很有创新性的算法，他可以证明某人知道某个秘密却不会泄露关于这个秘密的任何信息。这个算法可以解决什么问题呢？

它是对所有零知识证明问题的通用解决方法，由加密数字货币zcash首次使用并开源。zk-SNARK的优点：

1.通用库，可以解很多零知识证明问题

2.验证证明性能较高（300tps）

zk-SNARK的不足：

1.底层模型不容易理解，用户需要根据具体的零知识证明问题，在上层构建自己的业务模型，这块开发的工作量较大。

2.生成每笔交易时延较长（57s）

应用场景

ZKP的应用场景包括匿名可验证投票、数字资产安全交换、安全远程生物识别认证和安全拍卖，具体如下。

匿名可核查投票：投票是保障一个国家或控股公司民主的重要组成部分。然而，选民的隐私可能在投票过程中被泄露。此外，投票结果很难得到安全的核实。ZKP是实施匿名可核查投票的一种可用方法。根据ZKP的使用，符合条件的选民可以在不泄露身份的情况下投票表决显示他们的权利。此外，ZKP允许符合条件的选民要求提供可核查的证据，证明他们的选票包含在负责报告投票结果的机构的最终计票中。

数字资产的安全交换：数字资产是二进制数据的集合，它们是唯一可识别和有价值的。如果两个用户希望交换其数字资产，则用户的隐私，包括身份和交换数字资产的内容，可能会在交换过程中泄露。根据ZKP的使用，数字资产可以在不泄露用户隐私的情况下交换。此外，ZKP生成了可验证的证据，其中包含数字资产交换的过程。

安全远程生物识别身份验证：远程生物识别身份验证是一种可用于通过使用指纹、面部图像、虹膜或血管模式等生物识别模式识别用户访问权限的方法。但是，在实施远程生物识别认证时，用户的生物识别模式可能会泄露给不受信任的第三方。使用ZKP可以解决这个问题。此外，ZKP生成还提供了可核查的证据，其中包括识别用户访问权限的过程。

安全拍卖：政府拍卖是政府从多个供应商中选择最低出价的拍卖，这些供应商以竞争性方式销售其商品和服务。本次拍卖包括两个阶段。在第一阶段，多个供应商投标，但公众不知道。在第二阶段，这些投标是开放的。政府选择中标供应商，后者出价最低。然而，中标供应商的选择可能会泄露其他中标供应商的投标和身份。ZKP可以解决这个问题。ZKP为每个输标供应商生成可核查的证据。该证明证实输标供应商的投标与中标供应商的投标之间的差额是正的。

zk-snark应用于区块链的挑战及实现

零知识证明是指一方（证明者）向另一方（验证者）证明一个陈述是正确的，而无需透露除该陈述正确以外的任何信息，适用于解决任何NP问题。而区块链恰好可以抽象成多方验证交易是否有效（NP问题）的平台，因此，两者是天然相适应的。将零知识证明应用到区块链中需要考虑的技术挑战分为两大类：一类是适用于隐私保护的区块链架构设计方案，包括隐秘交易所花资产存在性证明、匿名资产双花问题、匿名资产花费与转移、隐秘交易不可区分等技术挑战；另一类是零知识证明技术本身带来的挑战，包括参数初始化阶段、算法性能以及安全问题等技术挑战。

华为集成了zksnark架构到区块链系统中来解决上面的挑战。我们知道有多种方法可以为区块链启用zkSNark。这些都降低了配对函数和椭圆曲线操作的实际成本。

1. 提高合约虚拟机的性能

相较第二种更难实现。可以在合约虚拟机中添加功能和限制，这将允许更好的实时编译和解释，而无需在现有实现中进行太多必要的更改。下面的转账场景就是基于此种方案的实现。

2. 仅提高某些配对函数和椭圆曲线乘法的在合约虚拟机的性能

通过强制所有区块链客户端实现特定的配对函数和在特定椭圆曲线上的乘法作为所谓的预编译契约来实现。好处是，这可能更容易和更快地实现。另一方面，缺点是我们固定在一定的配对函数和一定的椭圆曲线上。区块链的任何新客户端都必须重新实施这些预编译的合同。此外，如果有人找到更好的zkSNark、更好的配对函数或更好的椭圆曲线，或者如果在椭圆曲线、配对函数或zkSNark中发现缺陷，必须添加新的预编译合同。

转账应用

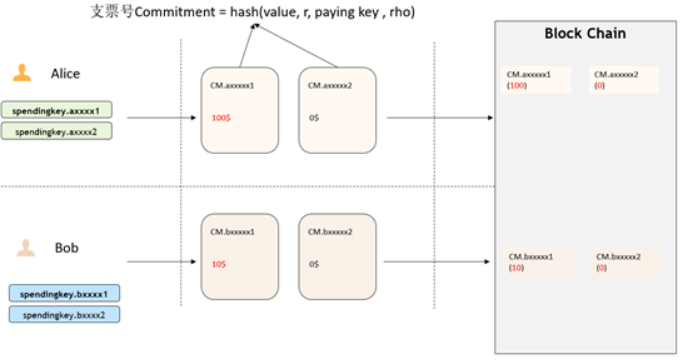
图6转账初始化

图6包含了对这个余额初始化的过程，生成交易也就是真正转账的过程包含验证，证明，完成验证，生成交易即收款等步骤。拿初始化举个例子，比如说爱丽丝初始化了一个100块钱的一个余额，然后鲍勃十块钱。转账的过程就可以描述为，爱丽丝转20块钱给鲍勃，内部生成一对Spending key / Paying Key ,相当于临时交易的一个账户，Paying Key给对方，Spending Key留给自己，用于证明交易链上的交易是属于谁的。

拿到生成的交易和相关的证明，就完成了交易生成这一步。下一步就要进行转账的验证证明，验证逻辑如下：

1. Nullifier NF.axxxxx1和NF.axxxxx2是否在Nullifiers列表中，也就是说，是否有被花过;
2. 验证NF.axxxxx1和NF.axxxxx2是格式是否合法的花费凭据，且对应的commitment在链上(Proof + Merkle tree root)，这里有需要验证Merkle tree root在 是有效的;
3. 验证input == output金额守恒，即：100 + 0 = 80+0+20;
4. 数字范围满足要求：100-20 >0 && 20 > 0

过程验证完了以后就进入最后一步。完成验证还会做一些类似于交易内容的隐藏,身份隐藏，交易行为的隐藏，来保护整个的这个转账交易过程的安全性，包括做一些混淆电路的能力。混淆交易内容且加密，验证者并不知道使用链上是哪个Commitment作为输入，只知道没有被花过，且在链上。身份隐藏让其无法确定接收方是谁，交易行为隐藏让其无法确定这个交易是发送还是接收。基于安全性的保证，才能完成整个验证过程。最后生成交易，然后收款，整个转账过程就结束了。基于零知识证明的转账，被华为集成在零知识证明使用接口中。集成的零知识证明架构也能用来开发一些隐私之类的应用，实现区块链隐私保护的解决方案。

总结

交易隐私保护这块的技术应该是比较多的，零知识证明技术并不一定是一个最好的选择，在安全领域中还有很多诸如同态，秘密分享，不经意传输，或者基于TEE硬件的一些隐私保护能力，可以去做一些隐私保护。但是零知识证明其优点也是很显著，未来区块链的隐私保护仍然任重而道远，如何实现快速高效、可信的零知识证明算法以及如何实现能够抵抗量子计算的零知识证明算法，都是需要进一步解决的问题。基于线上我们提供的一些基本的能力，要是大家感兴趣，可以到之前的网址下载相应的代码示例。

审核编辑：汤梓红