引 言
在对本科生的教育过程中,有时会出现因学生成绩过低、学分过少,而出现留级甚至延迟毕业的现象,这对学校和学生均造成了一定的负面影响。通过对学生成绩数据的挖掘分析,可辅助教学管理,以便教师实施有效的教学活动,并刺激学生主动学习,帮助学生取得更好的成绩。
文献[1]利用数10种不同的神经网络结构对学生成绩进行预测。文献[2]通过不同的分类模型,利用学生的校园卡数据和成绩数据预测成绩,其中多层分类器(MLPC)的效果最好。文献[3]的研究中表明,传统教师讲授式课堂下学生的不及格率是学生主动学习的不及格率的1.5倍。因此,教师在教导学生相关的科目时,可以通过提供预测数据来及时警告,促进学生主动学习,从而降低不及格率。
文献[4]使用神经网络来预测学生的学习成绩,结果显示,用神经网络算法比用线性回归更准确。但在这项研究中,主要选择了网上学习的成绩来研究,没有涉及线下面对面的教育方式。文献[5]在分析中学生的成绩时,利用人工神经网络,从认知因素和心理因素两个角度对学生的成绩进行聚类。但心理因素的主观性过强,容易影响结果的准确性。
神经网络具有良好的学习性能,但也有较为明显的缺点:收敛速度较慢、易陷入局部最小。用进化算法优化神经网络可以在一定程度上解决此问题。其中,差分进化算法是一种高效的寻优算法,通过对个体差异的处理实现变异,适用于非连续不可微分或噪音较强的函数。文献[6]证明了优化后的 DE⁃BPNN 模型预测效果要优于 GA ⁃BPNN、CS⁃BPNN 和 PSO ⁃BPNN 模型。利用差分进化优化神经网络算法,也可以让运算结果精度更高。
为了对大学生成绩等级进行更精准的预测,本文提出一种自适应差分进化神经网络模型,并对比了遗传算法与差分进化算法的适应度曲线。结果表明,采用差分进化算法寻找最优权值阈值的效果较好。
1、自适应差分进化算法
自适应差分进化算法(Adaptive Differential EvolutionAlgorithm,ADE)是一种基于种群的全局搜索算法。常用的差分进化模式为 DE/rand/1/bin 和 DE/best/1/bin,第一种收敛速度慢于第二种,但第一种在种群的多样性上较好,第二种易陷入局部最小值[8]。为了保持良好的多样性,本文采用的模式为 DE/rand/1/bin,即随机选择当前种群的个体进行变异,差异向量个数为 1,且在交叉的模式中应用二项交叉。差分进化算法主要有以下几个步骤:种群初始化、变异、交叉、选择。本文引入自适应变异因子 F,其值随迭代次数的增加而减小。
2、 ADE 优化 BP神经网络算法
BP 神经网络的特点为误差反向传播,具有较强的鲁棒性和容错性,但在运算中容易陷入局部最小,收敛速度较低[9]。神经网络结构由输入层、隐含层、输出层三层组成。根据 Kolmogorov 定理[10]可知,隐含层层数为1 时,只要有足够多的神经元节点数,就可以任意精度逼近任意非线性连续函数。当输入层为 X1,X2,…,Xm,隐含层为 h1,h2,…,hn,输出层为 Y 时,网络拓扑结构如图 1所示。
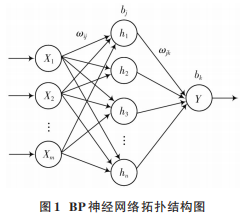
在该神经网络中,从输入层到隐含层的权值为ωij,阈值为bj,从隐含层到输出层的权值为ωjk,阈值为bk。其中,i=1,2,…,m;j=1,2,…,n;k=1。逐层传递输入信号后,在输出层计算预测值与实际值的误差。再根据所得误差,结合学习率 η,返回修改并更新权值与阈值。若迭代尚未结束,则进行下一代计算。
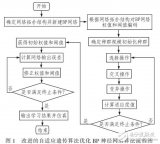
差分进化算法优化 BP 神经网络的原理为:将神经网络预测值与真实值的差值的均方误差作为适应度函数,最终得到适应度值最小时的权值阈值,并作为新的神经网络的权值阈值,最后进行求解。流程图如图 2所示。
3、 ADE⁃BP 神经网络学生成绩预测模型
3.1 数据预处理
为了便于后续数据的预测,并保证预测的准确性,首先要获得正确且合适的数据,因此需要对数据进行预处理。从学校的服务器中调取出 2016 级的学生成绩后,选择某个学院的学生成绩为本文的研究对象。提取出该学院所有学生从入学到大二下学期之间所有的课程成绩,再选择大三上学期的一门专业课成绩作为被预测对象。由于在学生的所有成绩中,“科目 h”这门课程的分数较低。为了凸显本模型的预测效果,并预防教学事故,本文将“科目 h”的分数等级作为被预测数据。数据库中的成绩庞杂且部分数据不完整,因此接下来需要提高数据质量,对数据进行预处理:数据清洗、数据集成、数据转换、数据归约。
1)数据清洗:去除空白数据和异常数据。
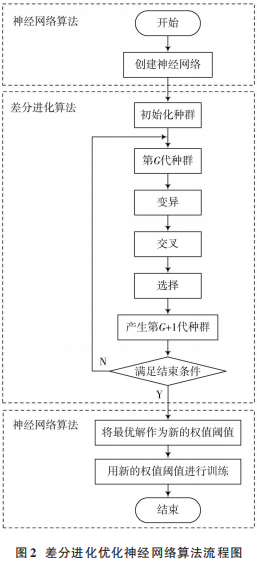
2)数据集成:将剩下的数据整理后,放在一个表格中,如表 1所示。
3)数据转换:由于数据集维数较高,为了降低神经网络的计算开销,本文在得到学生各科分数后,将学生成绩按照分数的不同层次划分为5个等级:分数<60分,等级为 0;60≤分数<70,等级为 1;70≤分数<80,等级为2;80≤分数<90,等级为 3;90≤分数<100,等级为 4。等级越高,该门科目的成绩越高,则该门科目的不及格率越低。
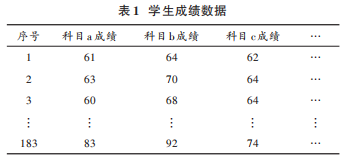
4)数据归约:由于原始数据量过于庞大,仅留下和“科目 h”的课程属性相同的科目,即均为“学科平台课程”的 8门科目。
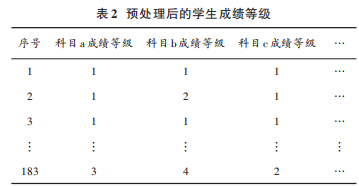
预处理后,得到 183条有效数据如表 2所示。
3.2 相关性分析
由于科目较多,为了简化网络结构,提高预测的效率,需要找出与被预测科目成绩最相关的科目,作为神经网络的输入。因此,本文首先通过 SPSS 对所有科目的成绩等级进行 Pearson 相关性分析。部分分析结果如表 3所示。
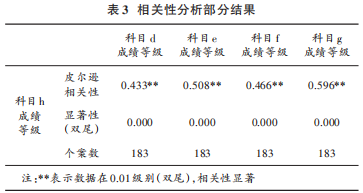
相关性分析的结果在 0.01级别显著,则认为有 99%的把握认为相关系数显著,该相关性分析结果具有统计学意义。由表 3 可知,本次相关性分析结果可以信任。本文选择与“科目 h”这门课程相关性系数大于 0.45 的科目分数作为输入数据,具体课程为:“科目 e”“科目 f”“科目 g”。
3.3 差分进化优化 BP神经网络进行预测
3.3.1 输入数据的归一化
本模型利用 Matlab 实现神经网络。首先将所有数据的顺序打乱,并随机选取 150 条作为训练数据,33 条作为测试数据。为了提高模型准确度,再将所有数据行归一化处理,使其值均在[-1,1]区间内。
3.3.2 输入层、输出层、隐含层节点数以及其他参数的选取
设置输入层数据是与“科目 h”相关性系数大于等于 0.45 的三门课程的成绩等级,输入层神经元节点数为 3;隐含层神经元节点数的设定需要经过多次测试,最终发现节点数为 9 时正确率最高,因此隐含层神经元数设为9;输出层为目标课程即“科目 h”的成绩等级,其神经元节点数为1。本文神经网络的隐含层节点转移函数选择 tansig 函数。输出层节点转移函数为 purelin函数。
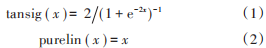
3.3.3 差分进化算法优化初始权值阈值
本模型中收敛误差设置为 0.01。由于学习速率过小会导致速度降低,学习率过大会导致权值震荡。结合经验,将学习速率 η设为 0.05。
为了使权值可以具有较快的收敛速度,同时求解精度较高,设定种群规模 NP为 50,最大迭代次数 Gm为 30,缩放因子 F 随迭代自适应变化,F 最小值为 0.2,最大值为 1.5,交叉因子 CR 为 0.9。所求问题的维数为:输入层节点数×隐含层节点数+隐含层节点数×输出层节点数+输入层节点数+输出层节点数。
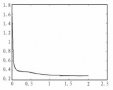
随机产生初始种群后,进行变异与交叉操作。在交叉操作中,有指数交叉与二项交叉两种方式。本文选用二项交叉。如果随机数大于 CR,则被选入新个体。再以神经网络训练出的预测值与真实值做差,其均方误差作为适应度函数。设置 GA⁃BP 的种群规模和最大迭代次数的值与 ADE⁃BP 的值一样,交叉概率为 0.9,变异概率为 0.2。图 3为差分进化优化 BP神经网络的适应度变化曲线,图 4 为遗传算法优化神经网络适应度变化的曲线。在达到最大迭代次数时,搜索出适应度值最小时的最优解。
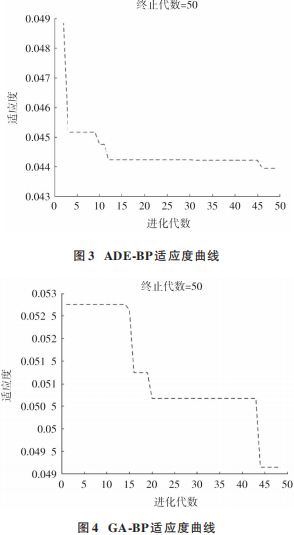
通过对比 ADE⁃BP 与 GA⁃BP 的适应度曲线,可以明显看出,用自适应差分进化优化 BP 神经网络的适应度下降更快,其误差均方差的值约为 0.044。而遗传算法优化神经网络所得到的均方误差值最终约为 0.049,可以看出,ADE⁃BP 的适应度更小,其均方差较小。因此可以得出,用自适应差分进化算法优化神经网络能更快、更好地找到函数的最优值。
3.3.4 赋予神经网络新的权值阈值并进行预测
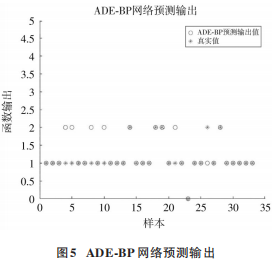
将搜索出的最优解转换为神经网络新的权值阈值,并对测试输入数据进行预测。由于本文将分数数据转换为 5 个等级,因此所有结果应为在区间[0,4]内的整数。因此对神经网络的输出值进行取整。设正确率为预测正确的数量与输出数据的数量的比值。本模型得到 的 正 确 数 量 为 27,输 出 数 据 总 共 33 个,正 确 率 为81.82%,MSE 为 0.181 8,并且误差值均为1,可见误差较小,认为预测效果较好。预测结果如图 5所示。
4 、结 论
本文利用ADE算法和GA算法分别对神经网络进行优化,可以看出,ADE 算法的收敛效果优于后者。利用学生的成绩数据,结合 Matlab 实现了基于自适应差分进化的学生成绩等级预测,并且该模型的预测效果较好。该模型在学生成绩的预测中具有较强的实际意义,不仅可以让学生进行有目的的主动学习、合理安排学习时间、提高科目的通过率,还能协助教师及时了解学生的学习情况,改善教学策略。在将来的研究中,可以进一步获取学生多方面的信息,并进行量化,对大学生的期末成绩进行深入研究。
审核编辑:郭婷
-
matlab
+关注
关注
185文章
2976浏览量
230526 -
神经网络
+关注
关注
42文章
4772浏览量
100801
原文标题:论文速览 | 基于自适应差分进化的学生成绩等级预测神经网络模型
文章出处:【微信号:现代电子技术,微信公众号:现代电子技术】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
如何构建神经网络?
卷积神经网络模型发展及应用
自适应遗传BP神经网络模型在统计建模中的应用
加工过程的神经网络模型参考自适应控制
一种改进的自适应遗传算法优化BP神经网络
基于反向学习的自适应差分进化算法
基于神经网络模型参考自适应实现混合动力汽车电子差速控制系统的设计




 基于自适应差分进化的学生成绩等级预测神经网络模型
基于自适应差分进化的学生成绩等级预测神经网络模型










评论